代码随想录算法训练营三期 day 23

代码随想录算法训练营三期 day 23 - 二叉树(9)

news2025/4/16 14:19:00

669. 修剪二叉搜索树

原文链接：669. 修剪二叉搜索树
题目链接：669. 修剪二叉搜索树
视频链接：669. 修剪二叉搜索树
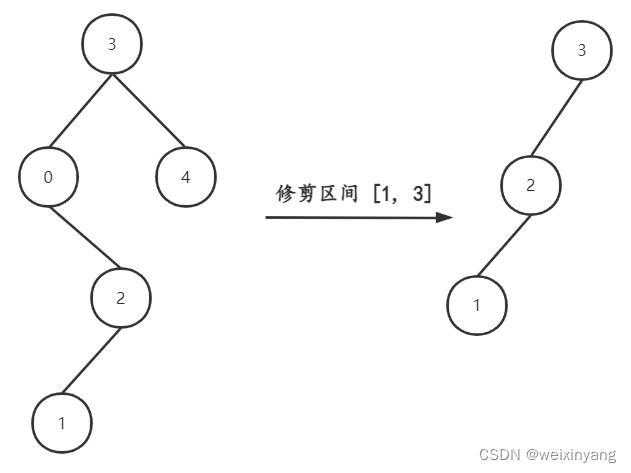
请添加图片描述
在上图中我们发现结点 $0$ 并不符合区间要求，那么将结点 $0$ 的右孩子结点 $2$ 直接赋给结点 $3$ 的左孩子就可以了（就是把结点 $0$ 从二叉树中移除）。

递归法

(1) 确定递归函数参数及返回值：
可以通过递归函数的返回值来移除结点。

    TreeNode* trimBST(TreeNode* root, int low, int high) {

(2) 确定终止条件：
遇到空节点返回。

        if (root == NULL) {
            return NULL;
        }

(3) 确定单层递归逻辑：
如果 $r o o t$ （当前结点）的数值小于 $l o w$ 的数值，那么应该递归右子树，并返回右子树符合条件的头结点。

        if (root -> val < low) {
            TreeNode* right = trimBST(root -> right, low, high);
            return right;
        }

如果 $r o o t$ （当前结点）的数值大于 $h i g h$ 的数值，那么应该递归左子树，并返回左子树符合条件的头结点。

        if (root -> val > high) {
            TreeNode* left = trimBST(root -> left, low, high);
            return left;
        }

接下来要将下一层处理完左子树的结果赋给 $root\rightarrow left$ ，处理完右子树的结果赋给 $root\rightarrow right$ 。
最后返回 $r o o t$ 结点，代码如下：

        root -> left = trimBST(root -> left, low, high);
        root -> right = trimBST(root -> right, low, high);
        return root;

请添加图片描述
在上图中：
如下代码相当于把结点 $0$ 的右孩子（结点 $2$ ）返回给上一层：

        if (root -> val < low) {
            TreeNode* right = trimBST(root -> right, low, high);
            return right;
        }

然后如下代码相当于用结点 $3$ 的左孩子把下一层返回的结点 $0$ 的右孩子（结点 $2$ ）接住。

        root -> left = trimBST(root -> left, low, high);

此时结点 $3$ 的左孩子就变成了结点 $2$ , 把结点 $0$ 删除了。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == NULL) {
            return NULL;
        }
        if (root -> val < low) {
            TreeNode* right = trimBST(root -> right, low, high);
            return right;
        }
        if (root -> val > high) {
            TreeNode* left = trimBST(root -> left, low, high);
            return left;
        }
        root -> left = trimBST(root -> left, low, high);
        root -> right = trimBST(root -> right, low, high);
        return root;
    }
};

总体代码如下：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == NULL) {
            return NULL;
        }
        if (root -> val < low) {
            TreeNode* right = trimBST(root -> right, low, high);
            return right;
        }
        if (root -> val > high) {
            TreeNode* left = trimBST(root -> left, low, high);
            return left;
        }
        root -> left = trimBST(root -> left, low, high);
        root -> right = trimBST(root -> right, low, high);
        return root;
    }
};

108. 将有序数组转换为二叉搜索树

原文链接：108. 将有序数组转换为二叉搜索树
题目链接：108. 将有序数组转换为二叉搜索树
视频链接：构造平衡二叉搜索树！| LeetCode：108. 将有序数组转换为二叉搜索树
有序数组构造二叉树，分割点就是数组中间位置的结点。
如果数组长度为偶数，中间结点有 $2$ 个，可以构成不同的平衡二叉树。

递归法

(1) 确定递归函数参数及返回值：
本题要构造二叉树，依然用递归函数的返回值来构造中结点的左右孩子。
参数：传入的数组，然后就是左下标 $l e f t$ 和右下标 $r i g h t$ 。

    // 左闭右闭区间 [left, right]
    TreeNode* traversal(vector<int>& nums, int left, int right)

注意定义的时候是左闭右闭区间，分割的时候也要坚持左闭右闭区间（循环不变量）。
(2) 确定终止条件：
因为是左闭右闭区间，所以当 $l e f t > r i g h t$ 的时候，就是空结点了。

        if (left > right) {
            return NULL;
        }

(3) 确定单层递归的逻辑：
寻找中间结点并构造中间结点:

        int mid = left + (right - left) / 2;
        TreeNode* root = new TreeNode(nums[mid]);

接着划分区间， $r o o t$ 的左孩子接住下一层左区间的构造结点，右孩子接住下一层右区间的构造结点。最后返回 $r o o t$ 结点。
单层递归整体代码如下：

        int mid = left + (right - left) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root -> left = traversal(nums, left, mid - 1);
        root -> right = traversal(nums, mid + 1, right);
        return root;

这里 int mid = left + ((right - left) / 2); 的写法相当于是如果数组长度为偶数，中间位置有两个元素，取靠左边的。
整体代码如下：

class Solution {
private:
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left > right) {
            return NULL;
        }
        int mid = left + (right - left) / 2;
        int rootValue = nums[mid];
        TreeNode* root = new TreeNode(rootValue);
        root -> left = traversal(nums, left, mid - 1);
        root -> right = traversal(nums, mid + 1, right);
        return root;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        TreeNode* root = traversal(nums, 0, nums.size() - 1);
        return root;
    }
};

538. 把二叉搜索树转换为累加树

原文链接：538. 把二叉搜索树转换为累加树
题目链接：538. 把二叉搜索树转换为累加树
视频链接：538. 把二叉搜索树转换为累加树
反中序遍历（右中左） 遍历二叉树，顺序累加即可。

递归法

需要 $p r e$ 指针记录当前遍历结点 $c u r$ 的前一个结点。
(1) 递归函数参数及返回值：
要遍历整棵树，递归函数不需要返回值。
需要一个全局变量 $p r e$ 来记录前一个结点的数值。

    int pre = 0;
    void traversal(TreeNode* cur) {

(2) 确定终止条件：

        if (cur == NULL) {
            return ;
        }

(3) 确定单层递归逻辑：
让 $c u r$ 加上前一个结点的值，并把 $c u r$ 的值赋给 $p r e$ 。

        traversal(cur -> right);            // 右
        cur -> val += pre;                  // 中
        pre = cur -> val;
        traversal(cur -> left);             // 左

代码如下：

class Solution {
private:
    int pre = 0;
    void traversal(TreeNode* cur) {
        if (cur == NULL) {
            return ;
        }
        traversal(cur -> right);            // 右
        cur -> val += pre;                  // 中
        pre = cur -> val;
        traversal(cur -> left);             // 左
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        traversal(root);
        return root;
    }
};

迭代法

代码如下：

class Solution {
private:
    int pre = 0;
    void traversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) {
                st.push(cur);
                cur = cur -> right;             // 右
            } else {
                cur = st.top();                 // 中
                st.pop();
                cur -> val += pre;
                pre = cur -> val;
                cur = cur -> left;              // 左
            }
        }
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        traversal(root);
        return root;
    }
};