235. 二叉搜索树的最近公共祖先
原文链接:235. 二叉搜索树的最近公共祖先
题目链接:235. 二叉搜索树的最近公共祖先
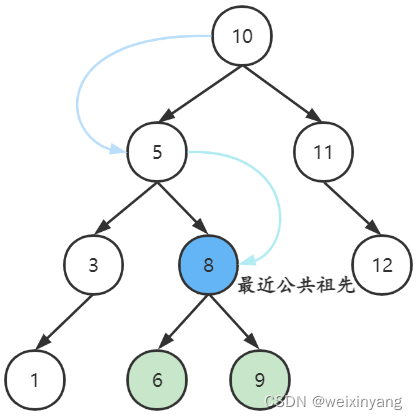
在 有序树 里:
从上向下递归遍历,第一次遇到
c
u
r
cur
cur 结点的数值在
p
,
q
p, q
p,q 结点对应数值的闭区间中,那么
c
u
r
cur
cur 就是
p
p
p 和
q
q
q 的最近公共祖先。
递归
(1) 确定递归函数参数及返回值:
参数:当前结点
c
u
r
cur
cur 以及
p
p
p,
q
q
q;
返回值:最近公共祖先
T
r
e
e
N
o
d
e
∗
TreeNode*
TreeNode∗;
TreeNode* lowestCommonAncestor(TreeNode* cur, TreeNode* p, TreeNode* q) {
(2) 确定终止条件:
if (cur == NULL) {
return cur;
}
(3) 确定单层递归逻辑:
如果
p
→
v
a
l
<
c
u
r
→
v
a
l
&
&
q
→
v
a
l
<
c
u
r
→
v
a
l
p \rightarrow val < cur \rightarrow val \ \&\&\ q \rightarrow val < cur \rightarrow val
p→val<cur→val && q→val<cur→val, 说明目标区间在左子树上,向左遍历。
如果
p
→
v
a
l
>
c
u
r
→
v
a
l
&
&
q
→
v
a
l
>
c
u
r
→
v
a
l
p \rightarrow val > cur \rightarrow val \ \&\&\ q \rightarrow val > cur \rightarrow val
p→val>cur→val && q→val>cur→val, 说明目标区间在右子树上,向右遍历。
由于 本题只需要搜索到一条符合条件的边 ,所以遇到递归函数的返回值不为空直接返回即可。
剩下的情况,就是
c
u
r
cur
cur 结点的数值在
p
,
q
p, q
p,q 结点对应数值的闭区间中,那么
c
u
r
cur
cur 就是
p
p
p 和
q
q
q 的最近公共祖先,返回
c
u
r
cur
cur 即可。
if (p -> val < cur -> val && q -> val < cur -> val) {
TreeNode* left = lowestCommonAncestor(cur -> left, p, q);
if (left != NULL) {
return left;
}
}
if (p -> val > cur -> val && q -> val > cur -> val) {
TreeNode* right = lowestCommonAncestor(cur -> right, p, q);
if (right != NULL) {
return right;
}
}
return cur;
代码如下:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* cur, TreeNode* p, TreeNode* q) {
if (cur == NULL) {
return cur;
}
if (p -> val < cur -> val && q -> val < cur -> val) {
TreeNode* left = lowestCommonAncestor(cur -> left, p, q);
if (left != NULL) {
return left;
}
}
if (p -> val > cur -> val && q -> val > cur -> val) {
TreeNode* right = lowestCommonAncestor(cur -> right, p, q);
if (right != NULL) {
return right;
}
}
return cur;
}
};
迭代
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* cur, TreeNode* p, TreeNode* q) {
while (cur) {
if (p -> val < cur -> val && q -> val < cur -> val) {
cur = cur -> left;
} else if (p -> val > cur -> val && q -> val > cur -> val) {
cur = cur -> right;
} else {
return cur;
}
}
return NULL;
}
};
701. 二叉搜索树中的插入操作
原文链接:701. 二叉搜索树中的插入操作
题目链接:701. 二叉搜索树中的插入操作
递归法
(1) 确定递归函数参数及返回值:
参数就是根节点指针,以及要插入元素。
递归函数的返回类型为
T
r
e
e
N
o
d
e
∗
TreeNode *
TreeNode∗, 可以利用返回值完成新加入的结点与其父结点的赋值操作。
TreeNode* insertIntoBST(TreeNode* root, int val) {
(2) 确定终止条件:
终止条件就是遍历的结点为
N
U
L
L
NULL
NULL 的时候,就是要插入结点的位置了,并把插入的结点返回。
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
这里把添加的结点返回给上一层,就完成了父子结点的赋值操作了。
(2) 确定单层递归逻辑:
搜索树是有序树,可以根据插入元素的数值,决定递归方向,
下一层将加入结点返回,本层用
r
o
o
t
→
l
e
f
t
root \rightarrow left
root→left 或者
r
o
o
t
→
r
i
g
h
t
root \rightarrow right
root→right 将其接住。
if (val < root -> val) {
root -> left = insertIntoBST(root -> left, val);
}
if (val > root -> val) {
root -> right = insertIntoBST(root -> right, val);
}
return root;
代码如下:
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
if (val < root -> val) {
root -> left = insertIntoBST(root -> left, val);
}
if (val > root -> val) {
root -> right = insertIntoBST(root -> right, val);
}
return root;
}
};
迭代法
在迭代法遍历的过程中,需要记录一下当前遍历的结点的父结点,这样才能做插入结点的操作。
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
TreeNode* cur = root;
TreeNode* parent = root;
while (cur != NULL) {
parent = cur;
if (val < cur -> val) {
cur = cur -> left;
} else if (val > cur -> val) {
cur = cur -> right;
}
}
TreeNode* node = new TreeNode(val);
if (val < parent -> val) {
parent -> left = node;
} else if (val > parent -> val) {
parent -> right = node;
}
return root;
}
};
450. 删除二叉搜索树中的节点
原文链接:450. 删除二叉搜索树中的节点
题目链接:450. 删除二叉搜索树中的节点
递归
(1) 确定递归函数参数及返回值:
可以借助递归函数返回值来删除结点。
TreeNode* deleteNode(TreeNode* root, int key) {
(2) 确定终止条件:
没找到要删除的结点,遍历到空直接返回:
// 1. 没找到删除的结点,遍历到空结点直接返回了
if (root == NULL) {
return root;
}
(3) 确定单层递归逻辑:
有以下五种情况:
(1) 没找到删除的结点,遍历到空结点直接返回了;
(2) 找到删除的结点:
i. 左右孩子都为空(叶子结点),直接删除结点, 返回
N
U
L
L
NULL
NULL 为根结点;
ii. 删除结点的左孩子为空,右孩子不为空,删除结点,右孩子补位,返回右孩子为根结点;
iii. 删除结点的右孩子为空,左孩子不为空,删除结点,左孩子补位,返回左孩子为根结点;
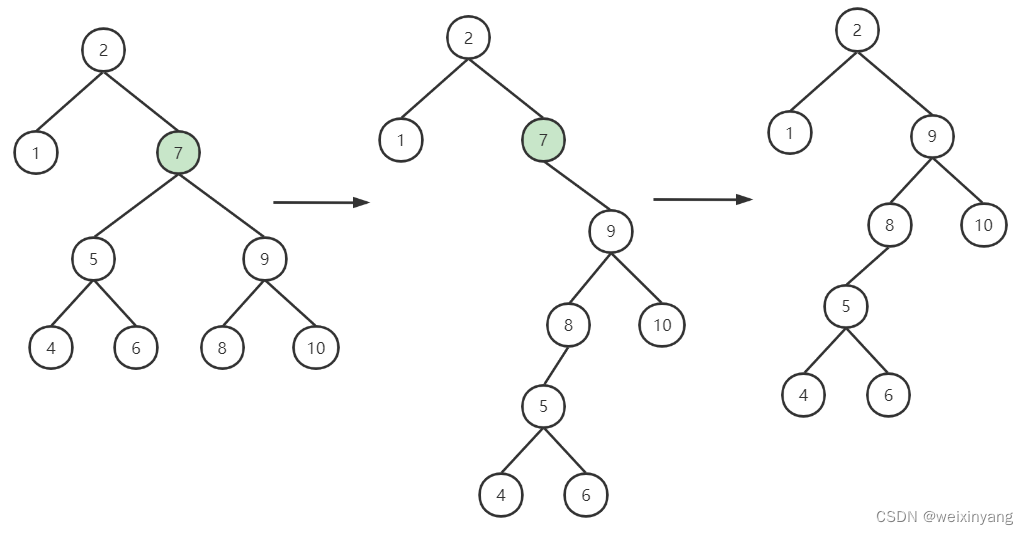
iv. 左右孩子结点都不为空,则将删除结点的左子树头结点(左孩子)放到删除结点的右子树的最左面结点的左孩子上,返回删除结点右孩子为新的根结点,如下图:
// 1. 没找到删除的结点,遍历到空结点直接返回了
if (root == NULL) {
return root;
}
// 2. 找到删除的结点
if (key == root -> val) {
// (1) 左右孩子都为空,直接删除结点,返回空结点
if (root -> left == NULL && root -> right == NULL) {
delete root;
return NULL;
}
// (2) 左孩子为空,右孩子不为空,返回右孩子
else if (root -> left == NULL) {
TreeNode* tmp = root -> right;
delete root;
return tmp;
}
// (3) 左孩子不为空,右孩子为空,返回左孩子
else if (root -> right == NULL) {
TreeNode* tmp = root -> left;
delete root;
return tmp;
}
// (4) 左右孩子都不为空
else {
// 找右子树最左边的结点
TreeNode* cur = root -> right;
while (cur -> left != NULL) {
cur = cur -> left;
}
// 把要删除的结点 (root) 的左子树放在 cur 的左孩子位置
cur -> left = root -> left;
TreeNode* tmp = root;
root = root -> right;
delete tmp;
return root;
}
}
这里相当于把新的结点返回给上一层,上一层就要用 r o o t → l e f t root \rightarrow left root→left 或者 r o o t → r i g h t root \rightarrow right root→right 接住,代码如下:
if (key < root -> val) {
root -> left = deleteNode(root -> left, key);
}
if (key > root -> val) {
root -> right = deleteNode(root -> right, key);
}
return root;
总体代码如下:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 1. 没找到删除的结点,遍历到空结点直接返回了
if (root == NULL) {
return root;
}
// 2. 找到删除的结点
if (key == root -> val) {
// (1) 左右孩子都为空,直接删除结点,返回空结点
if (root -> left == NULL && root -> right == NULL) {
delete root;
return NULL;
}
// (2) 左孩子为空,右孩子不为空,返回右孩子
else if (root -> left == NULL) {
TreeNode* tmp = root -> right;
delete root;
return tmp;
}
// (3) 左孩子不为空,右孩子为空,返回左孩子
else if (root -> right == NULL) {
TreeNode* tmp = root -> left;
delete root;
return tmp;
}
// (4) 左右孩子都不为空
else {
// 找右子树最左边的结点
TreeNode* cur = root -> right;
while (cur -> left != NULL) {
cur = cur -> left;
}
// 把要删除的结点 (root) 的左子树放在 cur 的左孩子位置
cur -> left = root -> left;
TreeNode* tmp = root;
root = root -> right;
delete tmp;
return root;
}
}
if (key < root -> val) {
root -> left = deleteNode(root -> left, key);
}
if (key > root -> val) {
root -> right = deleteNode(root -> right, key);
}
return root;
}
};