一、前言
Matlab的名称来源于“矩阵实验室(Matrix Laboratory)”,其对矩阵的操作具有先天性的优势(特别是相对于C语言的数组来说)。在数字图像处理和机器视觉实践中,为了提高编程效率,MATLAB 提供了多种方式来创建特殊的矩阵,如全零矩阵、全1矩阵、单位矩阵、空矩阵个、序列矩阵、稀疏矩阵、随机矩阵等。这些函数在图像模拟、统计分析、优化算法等多个领域都有广泛的应用。通过调整参数和结合MATLAB的其他功能,可以灵活地生成各种满足特定数字图像处理需求的随机矩阵。为了更好地快速掌握这里特殊矩阵的使用,每个矩阵后都附有实例,便于大家学习和交流。
二、特殊矩阵的生成及应用
1.全零矩阵
元素全为零的矩阵称为全零矩阵,MATLAB可以使用zeros创建全零矩阵。如zeros(5),生成一个5×5的矩阵元素全为零的方阵,而zeros(3,4)则生成3×4的矩阵元素全为零的矩阵


注意:如果使用zeros生成全零矩阵,其在MATLAB图像显示是黑色。
>> I=zeros(256,256);
>> imshow(I),title('全零矩阵图像')

2.全1矩阵
元素全为1的矩阵称为全1矩阵,MATLAB可以使用ones创建全1矩阵。如ones(5),生成一个5×5的矩阵元素全为1的方阵,而ones(3,4)则生成3×4的矩阵元素全为1的矩阵。


注意:如果一个矩阵是全1矩阵,其在MATLAB图像显示是白色。
>> onesMatrix=ones(256,256);
>> figure,imshow(onesMatrix),title(‘全1矩阵’)
>> whos onesMatrix


矩阵元素的数据类型为double,一个像素占8个Bytes。
3.单位矩阵
如果一个方阵对角线上的元素全为1,而其他的元素全为零则称单位矩阵,MATLAB可以使用eys创建单位矩阵。
如eye(5),生成一个5×5的单位矩阵。
I=eye(5);
figure,imshow(I)
whos I


矩阵元素的数据类型为double。
4. 空矩阵
空矩阵是指有一个或多个等于零的维度(0×0,0×1,1×0)
示例:
emptyMatrix=[] %创建空矩阵
size(emptyMatrix) %行列数都为0
length(emptyMatrix) %矩阵长度为0
numel(emptyMatrix) %元素个数为0
isempty(emptyMatrix) %判断是否为空矩阵,返回逻辑值1(真)
5. 序列矩阵
在MATLAB中创建一个序列矩阵,可以使用冒号操作符 : 或者函数 linspace 和 meshgrid。以下是一些示例:
5.1 创建一个1到20间隔为2的序列矩阵(从1开始):
1)使用冒号操作符 “:”创建
>> A = 1:2:20;

2) 使用linspace函数创建
>> A=linspace(1,19,10) %保存10个数据

5.2 生成一个二维网格采样点矩阵和生成三维曲面图
Matlab的meshgrid函数是用于生成网格坐标的函数,它可以将二维或三维数组作为输入,生成对应的网格坐标矩阵。这个函数在绘制三维图形、进行数值分析等方面有着广泛的应用。
语法格式: meshgrid(x, y)或meshgrid(X,Y,Z)
其中,x和y可以是任何一维或二维数组,分别表示x轴和y轴的坐标;X和Y可以是任何一维或二维数组,表示x轴和y轴坐标的范围;Z是可选的,如果提供,则生成三维图形的网格坐标矩阵。
示例1-生成二维网格采样点矩阵并绘制其矩阵点图
%使用meshgrid生成二维矩阵点并绘制二维坐标点图
clear all;
close all;
clc;
x=1:3;y=2:5;
[X,Y]=meshgrid(x,y)
plot(X,Y,'+','LineWidth',2,'Color','r'),title('显示meshgrid生成的二维网格点');
xlim([-2,5]);
ylim([-2,6]);
grid on
上面程序运行结果如下所示:




由上可知X和Y都是3行4列的矩阵,X矩阵的每一列值相同,分别是1、2和3,Y矩阵的每一行值都相同,分别是2、3、4和5,这是因为MATLAB的坐标原点是左上角,X正方向水平向右,Y正方向垂直向下。
示例2-生成三维曲面图:
[X,Y] = meshgrid(-2:.2:2, -4:.4:4);
Z = X .* exp(-X.^2 - Y.^2);
surf(X,Y,Z)%创建三维曲面图

6. 稀疏矩阵
稀疏矩阵—在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非0元素数目占大多数时,则称该矩阵为稠密矩阵。MATLAB提供了sparse函数来创建稀疏矩阵。在MATLAB中,创建一个稀疏矩阵可以通过sparse函数实现,该函数接受行索引、列索引和非零值作为输入,并生成一个稀疏矩阵。
以下是创建稀疏矩阵的示例代码:
% 定义行索引、列索引和对应的值
rows = [1; 3; 4; 5;6];
cols = [1; 2; 3; 4; 8];
values = [10; 20; 30; 35;40];
% 使用sparse函数创建稀疏矩阵
S = sparse(rows, cols, values);
% 显示稀疏矩阵
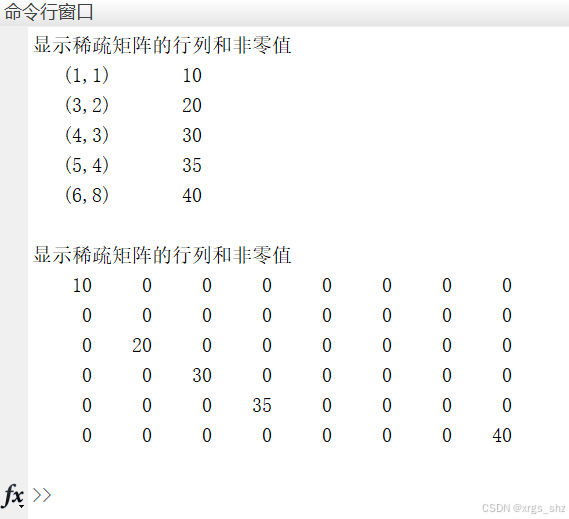
disp('显示稀疏矩阵的行列和非零值'),disp(S);
% 如果你想要看到稀疏矩阵的完整形式(包括零),可以使用full函数
disp('显示稀疏矩阵的完整形式'),disp(full(S));
上面程序运行结果如下:
7.随机矩阵
在MATLAB中,生成随机矩阵的常用函数是rand、randn、randi等。这些函数提供了不同的随机分布选项,以满足不同的应用需求,下面对上述各函数的含义和使用方法进行简要说明。
7.1 rand 函数
rand函数生成均匀分布的随机数。其基本语法是rand(n)生成一个n×n的矩阵,rand(m,n)生成一个m×n的矩阵,而rand(size(A))生成与矩阵A相同大小的矩阵。
应用实例:生成一个5×5的均匀分布随机矩阵,并计算其均值和标准差。
MATLAB程序代码如下:
% 生成5x5的随机矩阵并计算其均值和标准差
A = rand(5);
% 计算均值
%meanA = mean(A(:));
meanA=mean2(A);
% 计算标准差
%stdA = std(A(:));
stdA=std2(A);
disp('随机矩阵A:');
disp(A);
disp(['均值: ', num2str(meanA)]);
disp(['标准差: ', num2str(stdA)]);
运行结果如下图所示:

7.2 randn
randn(random normal distribution)是一种产生标准正态分布的随机数或矩阵的函数。randn函数生成标准正态分布的随机数(均值为0,标准差为1)。其语法与rand相同。
应用实例:生成一个10×10的标准正态分布随机矩阵,并计算其均值和标准差,并绘制其直方图以验证分布。
MATLAB程序代码如下:
% 生成10x10的标准正态分布随机矩阵
B = randn(10,10); %rand(10,10) 等价于rand(10)
meanB=mean2(B);
stdB=std2(B);
% 绘制直方图
figure;
histogram(B(:), 'Normalization', 'pdf');
title('标准正态分布随机矩阵的直方图');
xlabel('值');
ylabel('概率密度');
disp('随机矩阵B:');
disp(B);
disp(['均值: ', num2str(meanB)]); %数据(n*n)不足够多,均值不绝对为0
disp(['标准差: ', num2str(stdB)]); %数据(n*n)不足够多,标准差不绝对为1
![]()



7.3 randi 函数
在MATLAB命令提示符下,输入help randi就会显示如下帮助:
randi- Pseudorandom integers from a uniform discrete distribution.因此randi函数生成指定范围内的均匀分布的伪随机整数。其基本语法是randi([imin, imax])生成介于imin和 imax之间的随机整数(包含imin和imax),或者randi(imax)生成1到imax之间的随机整数。
应用实例:生成一个10×12的矩阵,其元素为0到7(每个像素占用3bit)之间的随机整数,并计算矩阵各行的和,矩阵的最小值,最大值和平均值,显示其数字图像和randi分布随机矩阵的直方图。
MATLAB程序代码如下:
%%randi的应用
% 生成10x12的随机整数矩阵
C = randi([0, 7], 10, 12);
% 计算每行的和
rowSums = sum(C, 2);
meanC=mean2(C); %计算其均值
minC=min(C(:)); %计算其最小值
maxC=max(C(:)); %计算其最大值
disp('随机整数矩阵C:');
disp(C);
disp('每行的和:');
disp(rowSums);
figure,imshow(C,[]);
figure;
histogram(C(:));
title('randi分布随机矩阵的直方图');
xlabel('灰度值');
ylabel('频数');
程序的部分运行结果如下:
randi生成的矩阵C如下:

矩阵C最大值maxC是7,最小值minC是0,平均值meanC是3.45(接近平均数(0+1+2+3+4+5+6+7)/8=3.5)。
矩阵C的图像显示如下图所示:

矩阵C的灰度直方图如下图所示:

由直方图也可以看出,该分布其接近于均匀分布。大家可以使用上面程序生成100x120的随机整数矩阵并进行图像分析(矩阵的最大值、最小值和平均值和直方图等)。