🏆🏆🏆🏆🏆🏆🏆
欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点✔★
蓝色文字表示：思路以及想法✔★
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！
　
我的qq号是：1210931886，欢迎大家加群，一起学习，互相交流，共同进步🎉🎉✨✨
🥇🥇🥇🥇🥇🥇🥇

蓝桥杯系列，为大家提供

做题全集，备战蓝桥杯，就做这个系列的题即可
一个大概的做题规划——大家最好在此基础上提前两个月准备

备战蓝桥杯就刷这些题
第一天博客链接
第二天博客链接

备战（蓝桥杯）算法竞赛-第1天

一、快速排序
- - - 1. 快速排序例题
    - 2. 第k个数( 快速选择 )
二、归并排序
- - - 1. 归并排序模板题
    - ★2. 逆序对的数量
三、二分
- - - 1. 数的范围
    - ★2. 数的三次方根
四、高精度
- - - 1. 高精度加法
    - 2. 高精度减法
    - 3. 高精度乘法
    - 4. 高精度除法 10：25-10：37(12分钟)
五、前缀和
- - - 2. 前缀和 (2分钟)
    - 3. 子矩阵的和（7分钟）

一、快速排序

1. 快速排序例题

原题链接

#include<iostream>
using namespace std;

void quick_sort(int a[],int r,int l)
{
    if(r >= l) return;
    
    int i = r - 1,j = l + 1,x = a[i + j >> 1];
    while(i < j)
    {
        do i++; while(a[i] < x);
        do j--; while(a[j] > x);
        if(i < j)swap(a[i],a[j]);
    }
    quick_sort(a,r,j),quick_sort(a,j+1,l);
}


int main()
{
    int n;
    cin >> n;
    int* a = (int*)malloc(sizeof(int)*n);
    for(int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    
    quick_sort(a,0,n-1);
    
    for(int i = 0; i < n; i++)
    {
        cout << a[i] << ' ';
    }
    return 0;
}

2. 第k个数( 快速选择 )

原题链接

#include<iostream>
using namespace std;

const int N = 1e6+10;

int a[N],k;

int quick_sort(int l,int r)
{
    if(l>=r)return a[r];
    int i = l-1,j = r+1,x = a[l+r>>1];
    while(i<j)
    {
        do i++;while(a[i]<x);
        do j--;while(a[j]>x);
        if(i<j)swap(a[i],a[j]);
    }
    if(j>=k)
        return quick_sort(l,j);
    else
        return quick_sort(j+1,r);
}

int main()
{
    int n;
    cin >> n >> k;
    for(int i = 1; i<= n; i++)
        cin >> a[i];
    
    cout << quick_sort(1,n);
}

二、归并排序

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

1. 归并排序模板题

原题链接

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100010;
int array[N];
int nums;
unsigned long result = 0;

void merge_sort(int array[], int l, int r)
{
    if (l >= r) return;
    int mid = ( l + r  ) / 2;
    merge_sort(array, l, mid);
    merge_sort(array, mid + 1, r);
    int temp[r - l + 1];
    int lptr = l;
    int rptr = mid + 1;
    int tempptr = 0;
    while(lptr <= mid && rptr <= r)
    {
        if(array[lptr] <= array[rptr])
        {
            temp[tempptr++] = array[lptr++];
        } else {
            temp[tempptr++] = array[rptr++];
            result += (mid - lptr + 1);//注意这里，是直接加的，后面的不需要比较了。
        } 
    } 
    while ( lptr <= mid )
    {
        temp[tempptr++] = array[lptr++];
    }
    while ( rptr <= r )
    {
        temp[tempptr++] = array[rptr++];
    }
    for (int i = l, j = 0; i <= r; i ++, j ++)
    {
        array[i] = temp[j];
    }
}

int main(){
    scanf("%d", &nums);
    for(int i = 0; i < nums; i++)
    {
        scanf("%d", &array[i]);
    }
    merge_sort(array, 0, nums-1);
    cout << result;
    return 0;
}

★2. 逆序对的数量

原题链接

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int a[N], tmp[N];

LL merge_sort(int q[], int l, int r)
{
    if (l >= r) return 0;

    int mid = l + r >> 1;

    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else
        {
            res += mid - i + 1;
            tmp[k ++ ] = q[j ++ ];
        }
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    cout << merge_sort(a, 0, n - 1) << endl;

    return 0;
}

三、二分

1. 数的范围

原题链接

#include<iostream>
using namespace std;

int n = 100010;
int a[100010] = {0};
int q,k,m;
        int l,r,mid;
int main()
{
    
    cin >> q >> m;
    for(int i = 0; i < q; i++)
    {
        cin >> a[i];
    }
    
    while(m--)
    {
        int s;
        cin >> s;
        l = 0,r = q - 1,mid;
        while(l<r)
        {
            mid = (l + r) / 2;
            if(a[mid] >= s) r = mid;
            else l = mid + 1;
        }
        if(a[l] != s)cout << "-1 -1" << endl;
        else
        {
            cout << l << " ";
            l = 0,r = q - 1,mid;
            while(l<r)
            {
                 mid = (l + r + 1) / 2;
                 if(a[mid] <= s) l = mid;
                  else r = mid - 1;
            }
            cout << l << ' ' << endl;
        }
    }
    
    return 0;
}

★2. 数的三次方根

原题链接

#include<iostream>
using namespace std;

int main()
{
    double x;
    cin >> x;
    
    double l = -100,r = 100;
    while(r - l > 1e-8)
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= x) r = mid;
        else l = mid;
    }
    
    printf("%.6f",l);
    return 0;
}

四、高精度

1. 高精度加法

原题链接

#include<iostream>
#include<vector>
using namespace std;

vector<int> add(vector<int> &A,vector<int> &B)
{
    if(A.size() < B.size())
        return add(B,A);
    
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size(); i++)
    {
        t+=A[i];
        if(i<B.size()) t+=B[i];
        C.push_back(t % 10);
        t /= 10;    
    }
    if(t)
    C.push_back(t);
    return C;
}

int main()
{
    string a,b;
    cin >> a >>b;
    vector<int> A,B;
    for(int i = a.size() - 1; i >=0; i--)A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >=0; i--)B.push_back(b[i] - '0');
    
    auto C = add(A,B);
    
    for(int i = C.size() - 1; i >=0; i--)
    cout << C[i];
    
    
    return 0;
}

2. 高精度减法

原题链接
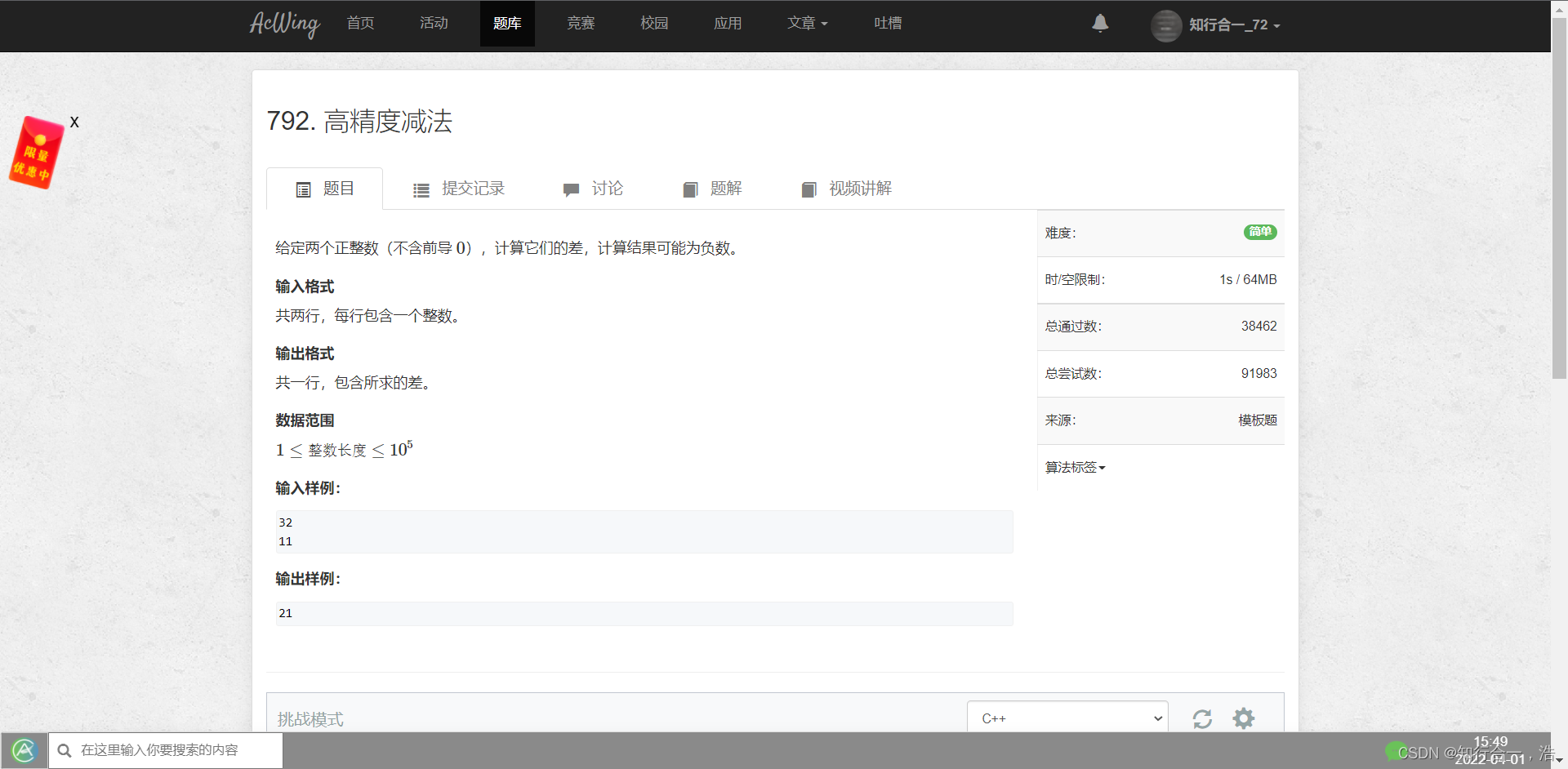
在这里插入图片描述
二刷：

小减大需要转换成大-小
如果出现负数 (x+10)%10 t = 1不是-1
t = a[i] - t; t = t - b[i]

#include <iostream>
#include <vector>

using namespace std;

bool cmp(vector<int> &A, vector<int> &B)
{
    if (A.size() != B.size()) return A.size() > B.size();

    for (int i = A.size() - 1; i >= 0; i -- )
        if (A[i] != B[i])
            return A[i] > B[i];

    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

    vector<int> C;

    if (cmp(A, B)) C = sub(A, B);
    else C = sub(B, A), cout << '-';

    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
    cout << endl;

    return 0;
}

3. 高精度乘法

原题链接

#include <iostream>
#include <vector>

using namespace std;


vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}


int main()
{
    string a;
    int b;

    cin >> a >> b;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

    return 0;
}

4. 高精度除法 10：25-10：37(12分钟)

原题链接

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

void div(vector<int> a,int b)
{
    vector<int> ans;
    
    int t = 0;
    for(int i = a.size()-1; i >= 0; i--)
    {
        t = t * 10 + a[i];
        ans.push_back(t/b);
        t = t-t/b*b;
    }
    
    reverse(ans.begin(),ans.end());
    
    while(ans.size()>1 && ans.back()==0)ans.pop_back();
    
    for(int i = ans.size()-1; i >=0; i--)
        cout << ans[i];
    cout << endl;
    cout << t;
    
}

int main()
{
    string s1;
    int b;
    vector<int>a;
    
    cin >> s1 >> b;
    
    for(int i = s1.size()-1; i >= 0; i--) a.push_back(s1[i]-'0');
    
    div(a,b);
    
    return 0;
}

五、前缀和

2. 前缀和 (2分钟)

原题链接

#include<iostream>

using namespace std;

const int N = 1e5+10;

int a[N],s[N];

int main()
{
    int n,m;
    
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        s[i] = a[i] + s[i-1];
    }
    
    while(m--)
    {
        int l,r;
        cin >> l >> r;
        
        cout << s[r] - s[l-1] << endl;
        
    }
    
    return 0;
}

3. 子矩阵的和（7分钟）

原题链接

#include<iostream>

using namespace std;

const int N = 1010;

int a[N][N],s[N][N];

int main()
{
    int n,m,q;
    cin >> n >> m >> q;
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
            s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];
        }

    while(q--)
    {
        int x1,y1,x2,y2;
        cin >> x1 >> y1 >> x2 >> y2;
        
        cout << s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1] << endl; 
        
    }
    
    
    
    return 0;
}