【基础篇】6 # 栈：如何实现浏览器的前进和后退功能？

news2024/11/19 3:36:36

说明

【数据结构与算法之美】专栏学习笔记

什么是栈？

栈是一种“操作受限”的线性表，只允许在一端插入和删除数据，其特性就是后进先出、先进后出。

栈既可以用数组来实现，也可以用链表来实现。

用数组实现的栈叫作顺序栈
用链表实现的栈叫作链式栈

支持动态扩容的顺序栈

如果要实现一个支持动态扩容的顺序栈，就需要底层依赖一个支持动态扩容的数组，当数组空间不够时，重新申请一块更大的内存，将原来数组中数据统统拷贝过去。

支持动态扩容的顺序栈的入栈、出栈操作的时间复杂度：

对于出栈操作：不会涉及内存的重新申请和数据的搬移，时间复杂度是 O(1)。
对于入栈操作：当栈中有空闲空间时，入栈操作的时间复杂度是 O(1)。当空间不够时，就需要重新申请内存和数据搬移，时间复杂度是 O(n)。

下面用摊还分析法分析入栈操作的时间复杂度：

先做一些假设和定义：

栈空间不够时，重新申请一个是原来大小两倍的数组；
只有入栈操作没有出栈操作；
定义不涉及内存搬移的入栈操作为 simple-push 操作，时间复杂度为 O(1)。

如果当前栈大小为 K，并且已满，当再有新的数据要入栈时，就需要重新申请 2 倍大小的内存，并且做 K 个数据的搬移操作，然后再入栈。后面的 K-1 次入栈操作，都不需要再重新申请内存和搬移数据，所以这 K-1 次入栈操作都只需要一个 simple-push 操作就可以完成。入栈操作的均摊时间复杂度就为 O(1)。

栈在函数调用中的应用

比较经典的一个应用场景就是函数调用栈。

操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构，用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

为什么函数调用要用“栈”来保存临时变量呢？用其他数据结构不行吗？

其实，我们不一定非要用栈来保存临时变量，只不过如果这个函数调用符合后进先出的特性，用栈这种数据结构来实现，是最顺理成章的选择。从调用函数进入被调用函数，对于数据来说，变化的是什么呢？是作用域。所以根本上，只要能保证每进入一个新的函数，都是一个新的作用域就可以。而要实现这个，用栈就非常方便。在进入被调用函数的时候，分配一段栈空间给这个函数的变量，在函数结束的时候，将栈顶复位，正好回到调用函数的作用域内。

栈在表达式求值中的应用

栈的另一个常见的应用场景，编译器如何利用栈来实现表达式求值。

编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。从左向右遍历表达式，当遇到数字，就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。如果当前操作符的优先级比栈顶的要高，说明这一操作符需要先执行，但是数据还没有准备好，因此先将操作符保存起来，等数据准备好了再执行；如果当前操作符的优先级比栈顶的要低，说明栈中的操作符需要先执行，那么先从数据栈中弹出两个数据，从操作符栈中弹出一个操作符，将这个结果先计算，并将计算出来的结果再入栈

栈在括号匹配中的应用

还可以用栈来检查表达式中的括号是否匹配。

如何检查包含三种括号（圆括号 ()、方括号[]、花括号{}）的任意嵌套表达式字符串是否合法呢？

可以使用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式。

如何实现一个栈？

下面是基于链表实现的栈：https://github.com/wangzheng0822/algo/blob/master/javascript/08_stack/StackBasedOnLinkedList.js

class Node {
    constructor(element) {
        this.element = element
        this.next = null
    }
}

export class StackBasedLinkedList {
    constructor() {
        this.top = null
    }
    push(value) {
        const node = new Node(value)
        if (this.top === null) {
            this.top = node
        } else {
            node.next = this.top
            this.top = node
        }
    }
    pop() {
        if (this.top === null) {
            return -1
        }
        const value = this.top.element
        this.top = this.top.next
        return value
    }
    // 为了实现浏览器前进后退
    clear() {
        this.top = null
    }
    display() {
        if (this.top !== null) {
            let temp = this.top
            while (temp !== null) {
                console.log(temp.element)
                temp = temp.next
            }
        }
    }
}

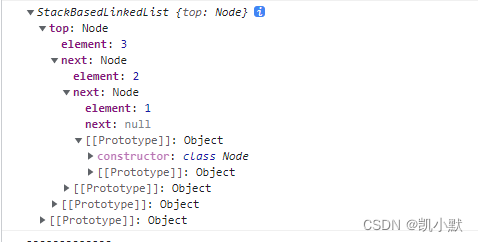
测试一下：

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>06.如何实现一个栈</title>
</head>
<body>
    <script type="module">
        import { StackBasedLinkedList } from "./js/06/StackBasedOnLinkedList.js";
        const newStack = new StackBasedLinkedList();
        newStack.push(1);
        newStack.push(2);
        newStack.push(3);
        console.log('-------------')
        console.log(newStack)
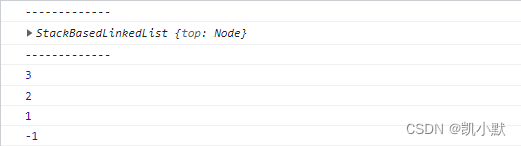
        console.log('-------------')
        console.log(newStack.pop());
        console.log(newStack.pop());
        console.log(newStack.pop());
        console.log(newStack.pop());
    </script>
</body>
</html>

在这里插入图片描述

如何实现浏览器的前进和后退功能？

使用前后栈实现浏览器的前进后退：https://github.com/wangzheng0822/algo/blob/master/javascript/08_stack/SampleBrowser.js

import * as Stack from "./StackBasedOnLinkedList.js"

export class SampleBrowser {
    constructor() {
        this.normalStack = new Stack['StackBasedLinkedList']()
        this.backStack = new Stack['StackBasedLinkedList']()
    }
    // 正常浏览页面
    pushNormal(name) {
        this.normalStack.push(name)
        this.backStack.clear()
    }
    // 后退
    back() {
        const value = this.normalStack.pop()
        if (value !== -1) {
            this.backStack.push(value)
        } else {
            console.log('无法后退')
        }
    }
    // 前进
    front() {
        const value = this.backStack.pop()
        if (value !== -1) {
            this.normalStack.push(value)
        } else {
            console.log('无法前进')
        }
    }
    // 打印栈内数据
    displayAllStack() {
        console.log('---后退页面---')
        this.backStack.display()
        console.log('---浏览页面---')
        this.normalStack.display()
    }
}

测试代码：

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>06.如何实现浏览器的前进和后退功能</title>
</head>
<body>
    <script type="module">
        import { SampleBrowser } from "./js/06/SampleBrowser.js";
        const browser = new SampleBrowser()
        browser.pushNormal("A页面")
        browser.pushNormal("B页面")
        browser.pushNormal("C页面")
        console.log(browser)
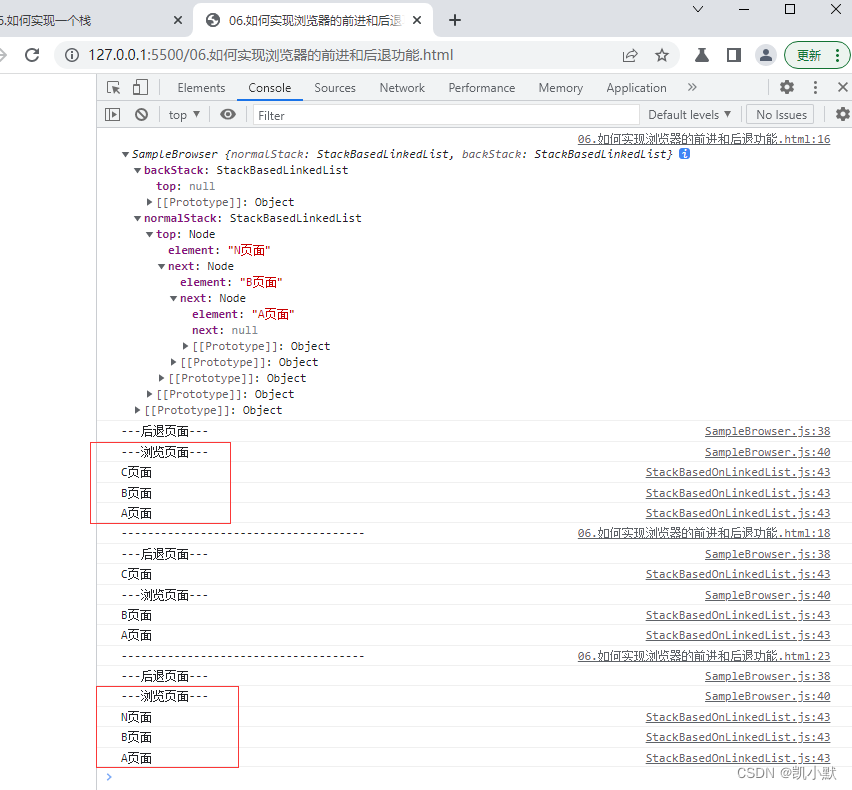
        browser.displayAllStack()
        console.log("-------------------------------------")
        browser.back()
        browser.back()
        browser.front()
        browser.displayAllStack()
        console.log("-------------------------------------")
        browser.pushNormal("N页面")
        browser.displayAllStack()
    </script>
</body>
</html>