其他题待补中……
链接：2023牛客寒假算法基础集训营5

简单题

A 小沙の好客（贪心，前缀和，二分）

题意思路

给定$n$个商品的价值，$q$次询问，每次询问$k,x$即价值不超过$x$的商品最多可以拿$k$个，问最多能拿的价值和最大是多少。
贪心的思考，我们肯定是拿价值越大的物品越好，所以最好从价值刚好等于$x$的物品开始往价值低的物品拿。首先我们排个序（升序），因为有$q$次询问肯定不能暴力的去遍历，我们容易想到二分去寻找价值不高于$x$的最接近的物品，之后再顺序往前取$k$个即可。
如何快速取得这一段的价值呢，因为是连续的$k$个商品，我们可以用前缀和来优化掉暴力遍历的取法。
需要注意：可能有价值相同的商品，所以我们每次需要得到最后一个价值不超过$x$的商品的位置，使用upper_bound函数取大于$x$的第一个再减1即为所求。

代码

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
const int N = 1e5 + 10;
int a[N];
ll pre[N];
int main()
{
    int n, q;
    scanf("%d%d",&n,&q);
    for(int i = 1; i <= n; i ++){
        scanf("%d",&a[i]);
    }

    sort(a + 1, a + 1 + n);

    for(int i = 1; i <= n; i ++){
        pre[i] += pre[i - 1] + a[i];//前缀和
    }

    for(int i = 1; i <= q; i ++){
        int k, x;
        scanf("%d%d",&k,&x);
        int idx = upper_bound(a + 1, a + 1 + n, x) - a;//取大于x的第一个元素的下标
        if(idx > n || a[idx] > x) idx --;
        int l = max(1, idx - k + 1), r = idx;//l防止越界，可能取不满k个
        printf("%lld\n",pre[r] - pre[l - 1]);
    }
    return 0;
}

B 小沙の博弈（贪心）

诈骗题……

题意思路

$n$堆石子，每次操作可以从桌子上拿走任意正整数个石子，将其置放于自己面前第一个没有石子的格子里。当桌上的石子数为 $0$ 时游戏结束，按照两人格子中石子数目组成序列的字典序判断胜负，字典序小的人获胜。
说是博弈，实际上每次取石子我们肯定只取一个放在当前格子里就跳到下一个格子，因为取$1$个是字典序最小的取法了，那么最后两人的序列都是$1,1,1,\dots \dots$，那么谁的序列短谁胜。易知当场上石子数$n$为偶数时两人序列一样长平局，为奇数时先手的多取一个序列更长后手胜。

代码

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
    int n;
    cin >> n;
    if(n & 1) puts("Yaya-win!");
    else puts("win-win!");
    return 0;
}

H 小沙の店铺（模拟）

题意思路

题目意思说的很清楚了，唯一需要注意的是：每次涨价都是在客户买完之后，即每个客户在购买时，价格不会变化。假设这个顾客买之前没满足涨价的条件，买到一半满足了，此时还是按涨价之前来算单价。

代码

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
int main()
{
    ll x, y, k, n, T;
    ll sum = 0;//卖出去总数
    ll val = 0;//卖出去的总价值
    cin >> x >> y >> k >> n >> T;
    for(int i  = n; i >= 1; i --){
        ll w = x + (sum / k) * y;//买之前的单件价格
        sum += i;//买的总数加上当前顾客买的
        val += w * i;//价值加上当前单价*当前顾客买的件数
        if(val >= T){
            printf("%d",n - i + 1);
            return 0;
        }
    }
    printf("-1");
    return 0;
}

K 小沙の抱团 easy（数学，贪心）

题意

当前人数为$n$,每次可以下达一个指令$x$,让$x$个人抱在一起，没人抱的人被淘汰，问如何下令才能让场上人数最少的同时下令次数最少。
实在不懂可以这样理解：给你一个数$n$，每次可以选择一个正整数，让$n=n-(n\mathrm{mod}x)$ $x<=n$。操作次数最少的同时让$n$变到最小。

思路

贪心的每次我们让更多的人出局最好，那么我们选定模数最好是就是当前人数$/2+1$，$x=n/2+1$。这样我们能让一半减一的人淘汰，没有比这更优的方法了。

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
int main()
{
    ll n;
    cin >> n;
    ll ans = 0;
    while(n > 2){
        ans ++;
        n = (n / 2 + 1);//等同于n -= (n % (n / 2 + 1))
    }
    cout << ans;
    return 0;
}

中档题

C 小沙の不懂（思维，分情况讨论）

出了点小意外，赛时ac的代码现在过不去了，应该是加了hack样例，之后看再补吧 ，赛时提交
hack样例：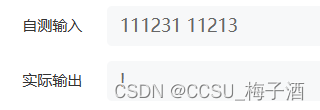
答案应该是 $>$ 。

已经更新，能AC了。

题意

给定$a,b$两个数字，还有一个未知的$0\sim 9$的排列，现在将$a,b$的每一位数字$ai=api,bi=bpi$变化后给出。问变化之前的数字
在$p$的任意一种排列中都有$a>b$ ，则输出$">"$。
在$p$的任意一种排列中都有$a<b$ ，则输出$"<"$。
在$p$的任意一种排列中都有$a=b$ ，则输出$"="$。
如果不满足以上任意一个条件则输出$"!"$。

思路

$0\sim 9$,$10$个不同数字的全排列有$3,628,800$种，而$a,b$的大小则有$10^{100000}$，我们肯定不能把每一种排列试一遍。其实我们只要思考一下就可以知道，只要转化后的两个数字不同，那么只要用不同的排列就可以让两个数字的大小发生变化。
例如：$a=1234和b=4321$ 假设排列就是$0,1,2,3,4$那么就没有变化还是$a>b$，如果排列是$0,4,3,2,1$那么两边就刚好互换过来$a=4321>b=1234$。
接下来我们分情况讨论，具体情况和注释都在代码中。

代码

#include <iostream>
#include <algorithm>
using namespace std;
string a, b;
int main()
{
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> a >> b;
    
    char ans = '>';//假定a更大
    if(a.length() < b.length()){
        ans = '<';//如果a更短，则为小于号
        swap(a, b);
    }
    int n = a.length();
    int m = b.length();


    if(a == b) {//相等就一定相等
        cout << "=";
        return 0;
    }
    
    if(n == m){//长度相等，但两者不等一定不确定答案
        cout << "!";
        return 0;
    }

    //因为排列不同，数字间的大小就变的无意义，在一个排列下大于的是小于，另一种排列大于的还是大于
    //长度不同，若无前导0则一定是长的大，所以我们假设a前面全是前导0最坏情况，看是否有可能 长的数 <= 短的数
    int id1 = 0;
    for(int i = 1; i < n; i ++){
        if(a[i] == a[0]) id1 = i;
        else break ;
    }
    
    //因为假设a前面全是前导0，所以若b前面数字相同的也是前导0也不能算
    int id2 = -1;
    for(int i = 0; i < m; i ++){
        if(b[i] == a[0]) id2 = i;
        else break;
    }

    int len1 = n - id1 - 1;//a最小情况下的有效长度
    int len2 = m - id2 - 1;//b最小情况下的有效长度

    if(len1 > len2){
        cout << ans;
    }
    else if(len1 == len2){//因为已经确定a[0]所代表的数字就是最小的0，所以还需要比较一下
        for(int i = 1; i <= len1; i ++){
            if(a[id1 + i] == b[id2 + i]) continue;
            if(b[id2 + i] == a[0]){
                cout << ans;
                return 0;
            }
            else break;//a可能更小
        }
        cout << "!";
    }
    else cout << "!";
    return 0;
}

D 小沙の赌气（贪心，思维，STL）

题意

发放$n$次道具，每次给小沙和小雅分别发一个道具给出的形式为$[l,r]$意为可以通过$[l,r]$的关卡，假设小沙和小雅都从第一关开始，他们必须一关一关通，只有通过了第 $x$ 关，第 $x+1$ 关才会解锁。他们可以将道具攒起来，到能使用道具的关卡再使用。每次发完道具后询问小沙小雅谁通关的多，多多少？

思路

因为道具可以攒起来，所以每次发完道具先看能不能使用，能用就用，不用我们就存储到一个容器里。放到什么容器中呢？假设我们当前关卡在$x$关，那么只有当道具卡$[l,r]$的$l<=x+1$才能使用，于是我们就想到了排序，就想到了优先队列按左端点排序，每次发完道具存进容器，查看容器顶部的道具能否使用，一直到不能使用为止。

代码

#include <queue>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct node{
    int l, r;
    bool operator < (const node &A)const{
        return l > A.l;
    }
}s1[N], s2[N];
priority_queue<node>q1, q2;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1; i <= n; i ++){
        scanf("%d%d",&s1[i].l, &s1[i].r);
    }
    for(int i = 1; i <= n; i ++){
        scanf("%d%d",&s2[i].l, &s2[i].r);
    }

    int res1 = 0, res2 = 0;
    for(int i = 1; i <= n; i ++){
        q1.push(s1[i]);//存入小沙的道具箱
        q2.push(s2[i]);//存入小雅的道具箱
        while(!q1.empty() && q1.top().l <= res1 + 1){
            res1 = max(res1, q1.top().r);//与右端点取max
            q1.pop();
        }
        while(!q2.empty() && q2.top().l <= res2 + 1){
            res2 = max(res2, q2.top().r);
            q2.pop();
        }
        if(res1 < res2){
            puts("ya_win!");
        }
        else if(res1 == res2){
            puts("win_win!");
        }
        else{
            puts("sa_win!");
        }
        printf("%d\n",abs(res1 - res2));
    }
    return 0;
}

L 小沙の抱团 hard（DP/记忆化搜索）

题意

与easy版本意思相同，但是指令不能随意下达，必须下达题目给定的$xi$，同时每个指令还有一个价值$bi$。每条指令可以重复使用。$n$个人，$m$条指令，$1<=n<=10^5,1<=m<=500$。花费代价最小的同时，人数剩下最少。

思路

我先贪心莽了一波，按每次淘汰的人数和价值，算出淘汰每个人的花费，使用平均花费最小的，但是不对，应该是这样可能无法使得人数剩下最少。于是我们决定采用优雅的暴力：记忆化搜索！先搜索出最多能淘汰多少人，再按淘汰的人数能够最多的情况下再搜索价值最少为多少。

代码

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
const int N = 1e5 + 10, M = 510;
const ll inf = 1e12;
struct node{
    int w, x;
    bool operator < (const node &A)const{
        return x < A.x;
    }
}s[N];
int n, m;
int f1[N],MAX;
ll f2[N];
int vis[N];
int dfs(int sum){
    if(f1[sum]) return f1[sum];
    for(int i = 1; i <= m; i ++){
        if(sum <= s[i].x) return f1[sum];
        if(sum % s[i].x == 0) continue ;
        f1[sum] = max(f1[sum], dfs(sum - (sum % s[i].x)) + sum % s[i].x);
    }
    return f1[sum];
}
ll dfs2(int sum){
	if(sum == n - MAX) return 0;
    if(n - sum + f1[sum] != MAX) return inf;//要能淘汰人数最多的方案
    if(vis[sum]) return f2[sum];//因为f2设置为无穷大，要用vis数组来代表有无搜索过
    vis[sum] = 1;
    for(int i = 1; i <= m; i ++){
        if(sum <= s[i].x) break;
        if(sum % s[i].x == 0) continue ;
        f2[sum] = min(f2[sum], dfs2(sum - (sum % s[i].x)) + s[i].w);
    }
    return f2[sum];
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= m; i ++){
        scanf("%d%d",&s[i].w,&s[i].x);
    }
    for(int i = 1; i <= n; i ++){
    	f2[i] = inf;//设置为无穷大
    }
    sort(s + 1, s + 1 + m);//排序
    
    MAX = dfs(n);//最多淘汰人数
    printf("%lld",dfs2(n));
    return 0;
}

I 小沙の金银阁（读题， 构造）

本题的重点是读题，读了十几遍才读明白，最后还半猜半蒙才过。建议把题面中标黑的部分多读几遍，出题人标黑是有原因的。

题意

有 $n$ 轮游戏，最开始有 $m$ 个灵石，每轮游戏可以下注不超过当前所有的灵石数，赢了则获得下注灵石数的两倍，否则输掉下注的灵石。即假设当前灵石数为 $sum$，下注 $x$ 灵石（$x<=sum$），若该轮赢则最终的灵石数为 $sum+x$,否则为 $sum-x$。已经提前知道，能赢且仅会赢一场，但不知道是哪一场会赢，赢了后你就会选择逃跑因为后面的游戏肯定会输。
询问：当能保证不亏灵石的情况下，最优下注方案是什么（方案灵石数加起来不能超过$m$），对于任意的另一个方案，在第 $X$ 轮获胜的时候，前 $X-1$ 轮，每轮结束之后剩余灵石相同，第 $X$ 轮获胜时总灵石越多，则该方案优于其它方案。如果不能保证不亏损则输出$-1$。

思路

首先要知道，你可能在任意一轮赢，所以你要保证你的方案能在不管哪一轮赢的情况下都不会亏损。 一开始读的几遍还以为是贪心，如果一开始就下注所有灵石，就会获得最多有$2m$ 个灵石，但这种下注在第一轮输之后再让你赢的情况中一开始就会吧钱输光，这是不合法的方案。

1.我们首先要构造出一种保证不会亏损的方案，我们假设第一轮下注$x$枚灵石，如果第一轮就赢显然不亏，如果输了那么我们就要考虑第二轮赢把第一轮的灵石赢回来的情况，就也要下注 $x$ 枚灵石，同理第三轮我们要考虑第三轮赢回前两轮输掉的灵石，下注 $2x$，以此类推每轮都要下注前一轮两倍的灵石数，第 $n$ 轮就需要下注 $x\ast 2^{n-1}$，$n$轮总共要下注 $x\ast 2^n$枚灵石。
因为要满足下注的所有灵石和不能超过 $m$，所以最小的合法方案就是当 $x=1$的时候，每次都只下注最低标准的灵石，如果 $m<2^n$ 则输出 $-1$,无合法方案。最小方案的构造方法是，每次只下注最小的满足金额，第一次下注 $1$，之后的每一轮都按照该轮会赢，且我们只赢回本金的方法下注。

2.当能保证不亏损时再去考虑如何更优，注意题目中所说的 前 $X-1$ 轮，每轮结束之后剩余灵石相同，第 $X$ 轮获胜时总灵石越多，则该方案优于其它方案。 我们从最小的方案开始想起，如何能更优的构造，假设前 $n-1$ 轮下注灵石相同，在最后一轮我们不下注 $2^{n-1}$ 而是下注更多，这样在第 $n$ 轮我们获胜的这一种情况下就会更优，其他轮获胜的情况相同。 同理向前推，第 $n-1$ 轮如果也下注更多在保证第 $n$ 轮能不亏本的情况下会更优。所以结论是在保证不亏的基础上，下注越多越好。
这样我们可以从后向前构造，假设当前灵石数为 $m$ 每次下注 $(m+1)/2$ 枚灵石。
为什么这样下注呢，下注后剩下的灵石数为 $m/2$，因为下注越多越好的原则，还剩下的 $m/2$ 枚灵石肯定会在之前下注中花完，这样该轮若胜利刚好保证不亏。

3.最后当这样构造完，可能仍然还剩下一些灵石，例如样例：

3 11
答案：2,2,6
构造出应该为 1,3,6

按照条件，若是第 $3$ 轮才赢，那么 $1,3,6$ 赚的灵石更多啊，再读一遍题目，觉得可能是 $X$ 越靠前的轮数先比较，若是第一轮赢则显然答案的方法更优，于是我就将还剩下的灵石全部下注到第一轮上 直到第二轮下注的灵石相同为止，实际上这样构造还剩下的灵石也不可能让第一轮的灵石数超过第二轮。 代码很简单，也有注释。

代码

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
const int N = 1e5 + 10;
ll pre[N];
ll a[N];
int main()
{
    ll n, m;
    cin >> n >> m;
    if(n == 1){//一轮必赢，我们就梭哈
        printf("%lld",m);
        return 0;
    }

    ll sum = 1;
    for(int i = 2; i <= n; i ++){//判断灵石数是否满足不亏
        sum <<= 1;
        if(sum > m){
            printf("-1");
            return 0;
        }
    }

    ll res = 0, t = m;
    for(int i = n; i >= 1; i --){//从后往前构造
        a[i] = (m + 1) / 2;
        m -= (m + 1) / 2;
        res += a[i];
    }
    a[1] += (t - res);//剩下的灵石加到a1上

    for(int i = 1; i <= n; i ++){
        printf("%lld ",a[i]);
    }
    return 0;
}

F 小沙の串串（单调栈）

题意

一个长度为 $n$ 的字符串，他有 $k$ 次操作，每次操作可以任意选择一个字符，将其移动到字符串的最后。 小沙想问你，找到恰好操作 $k$ 次之后，字典序最大的字符串是怎样的。
小诈骗：说是恰好 $k$ 次操作，实际上当你将字符串操作成降序也就是最大字典序后，若有操作次数没用完可以将剩下的操作次数用在末尾的字符上不改变字符串。

思路

首先每个字符最多只会被操作一次。
证明：假设某个字符 $ch1$ 被操作了两次，那么第二次操作说明 $ch1$ 的后面有比 $ch1$ 更大的字符 $ch2$,将 $ch1$ 换到最后会更优。
但是第一次操作 $ch1$ 时 $ch1$ 就已经在最后了，再操作 $ch2$ 将其放在 $ch1$ 的后面，但是我们可以将操作顺序换一下，先将操作 $ch2$，在操作 $ch1$ ,这样就能省下一次操作。
例如 $abc$ $k=2$ $ans=cba$
假如我们先操作 $a$，再操作 $b$ 此时 $string=cab$ 还需要一次操作，但我们可以先操作$b$ 再操作 $a$。
结论：任何需要两次操作来改变位置的，都可以通过调换第一次操作的顺序来省去第二次操作。

所以有当 $k>=n$ 我们可以直接得到一个降序（最大字典序）的字符串。
当 $k<n$，每次找当前最大的字符的位置，当操作数量允许时,将其前面的字符全部放到最后（可以放到一个临时字符串中，最后直接降序输出），再去找次大的字符,若操作数量不足，则也是去找次大的字符。

若当前最大字符所需的操作数不足时，此时次大字符可能在前面可能在后面如何寻找呢，不可能回过头去遍历时间复杂度不够。
正难则反，我们考虑从每个次大字符找右边更大的字符的位置。
我们可以用单调栈，对于每个字符我们记录其右边第一个比自己大的字符的位置，每次遍历到该位置若操作数支持遍历到更大的字符位置则向后遍历，否则该字符就是次大字符的位置。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int st[N], r[N];//r[i]:比字符s[i]大的右边的第一个字符的位置
int main()
{
    ios::sync_with_stdio(false);
    cout.tie(NULL);

    int n, k;
    string s;
    cin >> n >> k >> s;
    
    if(k >= n){
        sort(s.begin(), s.end(), greater<char>()); //降序
        cout << s;
        return 0;
    }

    int cnt = 0;
    for(int i = 0; i < n; i ++){
        while(cnt && s[st[cnt]] < s[i]) r[st[cnt --]] = i;
        st[++ cnt] = i;
    }

    string t1, t2;
    for(int i = 0; i < n; i ++){
        while(i < n && r[i] && r[i] - i <= k) t2 += s[i ++], k --;
        if(i < n) t1 += s[i];
    }

    if(k){ //需要注意，最后一个字符后面为空，所以要单独考虑是否要将其放到后面,还有操作次数没用就直接输出降序
        sort(s.begin(), s.end(), greater<char>()); //降序
        cout << s;
        return 0;
    }

    sort(t2.begin(), t2.end(), greater<char>());
    cout << t1 + t2;
    
    return 0;
}
/*
6 5
abcdea
edcbaa
*/