二叉树：删除二叉搜索树中的节点

news2024/11/19 5:46:59

删除二叉搜索树中的结点

一、题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

实例：

![[Pasted image 20230202120050.png]]

二、解题思路

我们删除一个结点，首先要找到这个结点，然而，寻找这个结点，会有两种情况：

1.没到了 2.没找到

对于1，没找到，说明树不会被修改，将原来的树原封不动返回。
对于2，找到了，肯定返回的是最终删除了指定元素的树。

这里对2进行重点分析，这个题的思路和递归代码相结合的时候，有些地方很难理解，一会在代码解析部分会重点讲解，这里重点理解思路

那对于每一个结点，我们是怎么处理的呢？

对于每一个结点，我们要分成四种情况：

当前结点是NULL ,说明已经找完了，找到叶子结点的孩子了，还是没有，那就返回NULL就行了
当前结点的val是key，那就要删除这个结点了，但是，删除结点还要保证二叉搜索树的结构
1. 当前结点左右子树都为空:直接删除这个结点，不用改变结构
2. 当前结点左子树不为空，右子树为空：用左子树替代当前结点
3. 当前结点左子树为空，右子树不为空：用右子树替代当前结点
4. 当前结点左右子树都不为空：
  1. 先将当前结点左子树，放在当前结点右子树的最左侧孩子的左子树位置上
  2. 用当前结点右子树代替当前结点
  3. 【为什么要这样操作？】
    1. 首先由于这是二叉搜索树，所以，当前结点左子树上所有元素都是小于当前结点右子树上最小元素的
    2. 当前结点右子树上最小元素就是当前结点右子树上最左侧的元素
    3. 所以，将左子树放在右子树最左侧结点的左子树位置是没有问题的
当前结点的val > key：说明目标key小于当前结点，所以要往当前结点左侧找
当前结点的val < key：说明目标key大于当前结点，所以要往当前结点的右侧找

上面就是对每个结点具体的操作步骤了。
那具体代码如何组织呢，看下面的解析：

三、代码解析

3.1 函数返回值和参数

这个题目是：删除二叉搜索树中的节点

那么如果删除了，我们期望的返回值就是，删除过指定节点之后的二叉树。
如果没删除，就返回一个空指针。

所以，这个函数的返回值是TreeNode*，二叉树节点指针类型。

参数，很明显，要传入这个树的根节点和目标值key

所以，函数返回值和参数如下

TreeNode* deleteNode(TreeNode* root, int key){
	//函数体
}

3.2 递归函数体

这里按照解题思路中的逻辑来处理代码

TreeNode* deleteNode(TreeNode* root, int key) {
		 //递归终止的条件：遍历完这个树，没有找到目标结点
        if (root == NULL) return root;
        
        //当遍历到的val == key时
        if (root->val == key) {
            //1.遍历到结点的左右子树都为空，
            //那直接删除这个结点，并向删除结点的父节点返回NULL，相当于是用NULl代替了删除结点
            if (root->left == NULL && root->right == NULL) {
                delete root;//删除结点
                return NULL;//向上一层返回NULL，代表用NULL代替了待删除结点
            }
            //2.遍历到结点左子树不为空，右子树为空，那用左子树来代替这个结点
            else if (root->right == NULL && root->left != NULL) {
                TreeNode* retNode = root->left;
                delete root;//删除结点
                return retNode;//向上一层返回刚才保存的左子树，
                //也可以理解为用左子树代替了待删除结点
            }
            //3.遍历到结点右子树不为空，左子树为空，那用右子树来代替这个结点
            else if (root->right != NULL && root->left == NULL) {
                TreeNode* retNode = root->right;
                delete root;//删除结点
                return retNode;//向上返回待删除结点右子树
            }
            //4.遍历到结点左右子树都不为空，
            //将左子树放在右子树的最左侧结点的左子树上，并用右子树代替待删除结点
            else {
                //找到右子树最左侧的结点
                TreeNode* cur = root->right;
                while (cur->left != NULL) {
                    cur = cur->left;
                }
                //将待删除结点的左子树放在右子树左侧结点的左子树上
                cur->left = root->left;
                //用tem暂存待删除结点，因为，一会要改变root的值
                TreeNode* tmp = root;//一会删除tmp就行了
                //用root的右子树替代root
                root = root->right;
                //删除原来的root
                delete tmp;
                //返回现在修改过后的root
                return root;
            }
        }

		//如果当前遍历结点大于key值,说明key在当前结点的左侧，往当前结案的左侧遍历
        if (root->val > key) root->left = deleteNode(root->left, key);
        //如果当前遍历结点小于key值，说明key在当前结点的右侧，王当前结点的右侧遍历
        if (root->val < key) root->right = deleteNode(root->right, key);

        return root;
}

这里用一个例子来展示一下代码是怎么运行的：

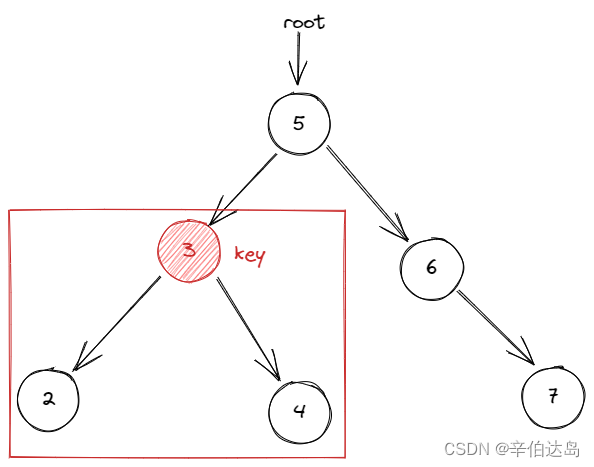
给出树的根节点是root,目标结点key是3，也就是要删除3这个结点。
现在代码开始运行：
判断当前root是不是NULL => 不是，不用执行return NULL
判断当前root->val是不是key => 不是，不用执行删除修改代码
判断当前root->val是不是大于key => 是，执行递归代码。

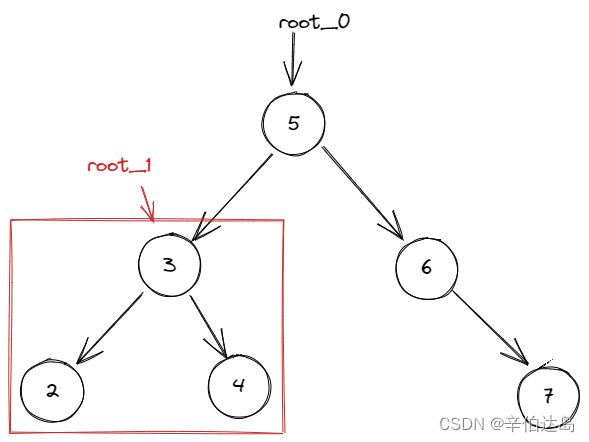
为了区分，我们将第一次调用递归函数传入的root称为root_0
将第二次调用递归函数传入的root称为root_1。
如果所示，
第一次传入的root_0当前是整个树的根节点。
按照代码执行流程，判断了root_0的val是大于key的，所以执行了相应的递归函数。
所以，第二次传入的root_1是根节点的左孩子。

那第二次递归函数做了哪些操作呢？

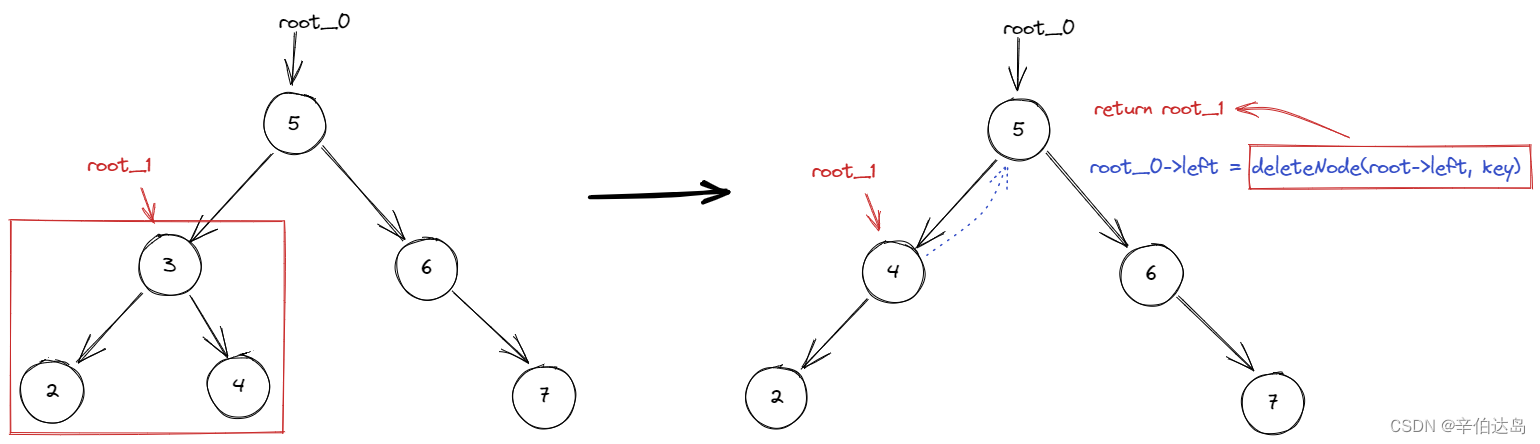
请添加图片描述

进入第二次调用函数传入root_1,那函数再次重头开始执行

判断当前roor_1是不是NULL => 不是，不执行return NULL
判断当前root_1的val是不是key3 => 是，指向判断里面的代码
判断当前root_1的左右是不是都有孩子 = > 执行左右孩子都存在的代码
返回修改过后的root_1

注意看上图

root_1是第二次调用递归函数所得到的结果，这个结果赋值给了第一次调用递归函数时root_0的左子树，那就相当于是将root_0的左子树修改成了删除后的样子。

最终返回root_0也就是返回整个树的根，代码执行完毕。

到这里就讲解完毕了，如果还是不明白，结合思路，代码，将这个例子自己理一遍思路。

对于开始接触递归的小伙伴，总是觉得思考起来很困难，很抽象。
就对于这个题来说，如果要找的key是1那应该怎么向上传值呢？

那按照同样的思路，最底下一层调用递归函数传入的参数会是2这个结点的左子树，也就是NULL。
然后会将NULL赋值给2的左子树。继续往执行，会返回2这个结点，将2这个结点赋值给结点3的左子树。
同样，向上返回3这个结点，将3这个结点返回给5的左子树。最后返回root。