【并发编程十四】c++原子操作(2)——实现自旋锁
- 一、自旋锁简介
- 二、使用自旋锁
- 三、不使用自旋锁
- 四、分析
- 简介
在介绍完原子操作,我们这篇使用c++提供的原子操作,实现一个自旋锁,并加以利用。
原子操作参见【并发编程十三】c++原子操作
一、自旋锁简介
“自旋”可以理解为“自我旋转”,这里的“旋转”指“循环”,比如 while 循环或者 for 循环。“自旋”就是自己在这里不停地循环,直到目标达成。而不像普通的锁那样,如果获取不到锁就进入阻塞
-
自旋锁(spinlock):是指当一个线程在获取锁的时候,如果锁已经被其它线程获取,那么该线程将循环等待,然后不断的判断锁是否能够被成功获取,直到获取到锁才会退出循环。
-
自旋锁,它并不会放弃 CPU 时间片,而是通过自旋等待锁的释放,也就是说,它会不停地再次地尝试获取锁,如果失败就再次尝试,直到成功为止
-
非自旋锁,非自旋锁和自旋锁是完全不一样的,如果它发现此时获取不到锁,它就把自己的线程切换状态,让线程休眠,然后 CPU 就可以在这段时间去做很多其他的事情,直到之前持有这把锁的线程释放了锁,于是 CPU 再把之前的线程恢复回来,让这个线程再去尝试获取这把锁。如果再次失败,就再次让线程休眠
非自旋锁和自旋锁最大的区别,就是如果它遇到拿不到锁的情况,它会把线程阻塞,直到被唤醒。而自旋锁会不停地尝试
二、使用自旋锁
#include <iostream>
#include<thread>
#include<mutex>
#include <atomic>
using namespace std;
class spinlock_mutex
{
public:
spinlock_mutex() {};
//spinlock_mutex(const spinlock_mutex& origin); // add this line
~spinlock_mutex() {};
void lock()
{
while (flag.test_and_set(memory_order_acquire));
}
void unlock()
{
flag.clear(memory_order_release);
}
private:
atomic_flag flag = ATOMIC_FLAG_INIT;
};
int g = 0;
spinlock_mutex mtx;
void task()
{
for (int i = 0; i < 5; i++)
{
lock_guard<spinlock_mutex> my_lock(mtx);
//mtx.lock();
g++;
cout << "task:g="<<g << endl;
//mtx.unlock();
}
}
int main()
{
//cout << "g"<<g << endl;
thread t1(task);
thread t2(task);
t1.join();
t2.join();
return 0;
}
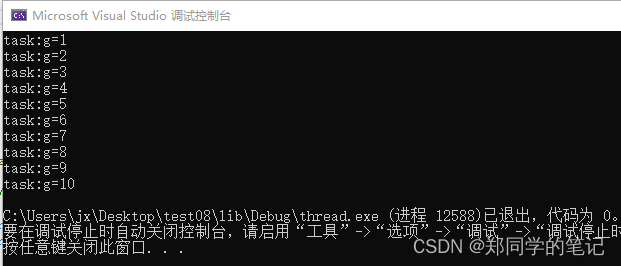
输出
三、不使用自旋锁
#include <iostream>
#include<thread>
#include<mutex>
#include <atomic>
using namespace std;
//class spinlock_mutex
//{
//public:
// spinlock_mutex()
// {
// }
//
// //spinlock_mutex(const spinlock_mutex& origin); // add this line
// ~spinlock_mutex() {};
//
// void lock()
// {
// while (flag.test_and_set(memory_order_acquire));
// }
// void unlock()
// {
// flag.clear(memory_order_release);
// }
//private:
// atomic_flag flag = ATOMIC_FLAG_INIT;
//};
int g = 0;
//spinlock_mutex mtx;
void task()
{
for (int i = 0; i < 5; i++)
{
// lock_guard<spinlock_mutex> my_lock(mtx);
//mtx.lock();
g++;
cout << "task:g="<<g << endl;
//mtx.unlock();
}
}
int main()
{
//cout << "g"<<g << endl;
thread t1(task);
thread t2(task);
t1.join();
t2.join();
return 0;
}
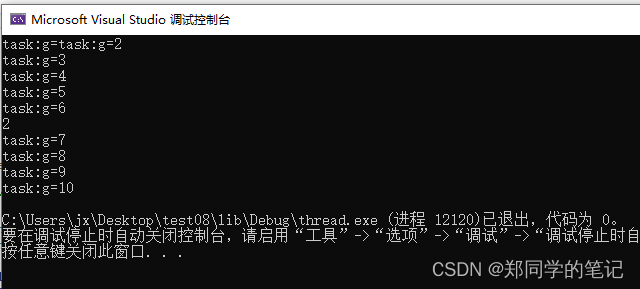
输出
四、分析
- 因为io是进程内共享的,所以当我们操作而不加锁时,会出现输出串行的现象。(说明我们实现的自旋锁可用、有效)
- 我们实现的自旋锁可以配合lock_guard使用;
- 当然我们也可以直接使用mtx.lock()、mtx.unlock();进行加锁和解锁。







![[Android开发基础3] Activity的生命周期、创建与配置](https://img-blog.csdnimg.cn/ed849be6fb564a2a9e8ddbb39200c8ca.png)