“生日悖论”简析——公式计算、代码模拟

“生日悖论”共享生日概率，通项公式计算，代码模拟计算。

(笔记模板由python脚本于2024年07月17日 18:16:40创建，本篇笔记适合会基础编程的coder翻阅)

【学习的细节是欢悦的历程】

Python 官网：https://www.python.org/
Free：大咖免费“圣经”教程《 python 完全自学教程》，不仅仅是基础那么简单……
地址：https://lqpybook.readthedocs.io/

自学并不是什么神秘的东西，一个人一辈子自学的时间总是比在学校学习的时间长，没有老师的时候总是比有老师的时候多。
—— 华罗庚

My CSDN主页、My HOT博、My Python 学习个人备忘录
好文力荐、老齐教室

求取共享生日概率 “生日悖论”简析 (公式计算、代码模拟计算)

本文质量分：

【 $96$ 】
本文地址： https://blog.csdn.net/m0_57158496/article/details/140502323

CSDN质量分查询入口：http://www.csdn.net/qc

目录

◆ “生日悖论”简析
- 1、繁复的“莫名”代码
- 2、ai解析
- 3、“生日悖论”的前世今生
- - 3.1 前世
  - - 起源
    - 数学原理
  - 3.2 今生
  - - 定义
    - 解答
    - 计算方法
    - 实际应用
    - 扩展和变体
  - 3.3 结论
- 4、我的“生日悖论”
- - 4.1 公式计算
  - 4.2 代码模拟
  - 4.3 ai点评
  - 优点：
  - 建议：
- 5、与ai学习搭子探讨优化
- - 5.1 优化代码
  - 5.2 ai点评
  - 代码点评
  - 5.3 代码文档
  - 5.4 代码运行效果截屏图片
- 6、感悟

◆ “生日悖论”简析

1、繁复的“莫名”代码

import datetime, random

def getBirthdays(numberOfBirthdays):
    birthdays=  
    for i in range(numberOfBirthdays):
        startOfYear = datetime.date(2001, 1, 1)
        randomNumberOfDays = datetime.timedelta(random.randint(0, 364))
        birthday = startOfYear + randomNumberOfDays
        birthdays.append(birthday)
    return birthdays

def getMatch(birthdays):
    if len(birthdays) == len(set(birthdays)):
        return None
    
    else:
        for a, birthdayA in enumerate(birthdays):
            for b, birthdayB in enumerate(birthdays):
                if birthdayA == birthdayB:
                    return birthdayA

MONTHS =  'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
          'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec' 

while True:
    print('How many birthdays shall I generate?(Max 100)')
    response = input('> ')
    if response.isdecimal() and (0 < int(response) <= 100):
        numBDays = int(response)
        break
print()

print('Here are', numBDays, 'birthdays:')
birthdays = getBirthdays(numBDays)
for i, birthday in enumerate(birthdays):
    if i != 0:
        print(', ', end='')
    monthName = MONTHS birthday.month-1 
    dateText = '{} {}'.format(monthName, birthday.day)
    print(dateText, end='')
print()
print()

match = getMatch(birthdays)
print('In this simulation, ', end='')
if match != None:
    monthName = MONTHS match.month-1 
    dateText = '{} {}'.format(monthName, match.day)
    print('multiple people have a birthday on ', dateText)
else:
    print('there are no matching birthdays.')
print()

print('Generating', numBDays, 'random birthdays 100000 time...')
input('Press Enter to begin...')

print("Let\'s run another 100000 simulations.")
simMatch = 0
for i in range(100_000):
    if i % 10_000 == 0:
        print(i, 'simulations run...')
    birthdays = getBirthdays(numBDays)
    if getMatch(birthdays) != None:
        simMatch += 1
print('100000 simulations run.')

probability = round(simMatch / 100_000 * 100, 2)
print('Out of 100,000 simulations of ', numBDays, ' people, there was a')
print('matchining birthday in that group', simMatch, 'times. This means')
print('that' , numBDays, ' people have a', probability, '% chance of')
print('having a matching birthday in their group.')
print('That\'s probaly more than you would think!')

if match != None:
    monthName = MONTHS match.month-1 
    dateText = '{} {}'.format(monthName, match.day)
    print('multiple people have a birthday on ', dateText)
else:
    print('there are no matching birthdays.')
print()

print('Generating', numBDays, 'random birthdays 100000 time...')
input('Press Enter to begin...')

print('Let\'s run another 100000 simulations.')
simMatch = 0
for i in range(100_000):
    if i % 10_000 == 0:
        print(i, 'simulations run...')
    birthdays = getBirthdays(numBDays)
    if getMatch(birthdays) != None:
        simMatch += 1
print('100000 simulations run.')

probability = round(simMatch / 100_000 * 100, 2)

这段代码截取于python学习QQ群，我不可以完全看懂其功用。但我却感觉书写得太繁复了些。所以求问了我的ai学习搭子。

回页目录

2、ai解析

这段代码是在模拟著名的“生日悖论”问题，即在一个随机选取的群体中，至少有两个人在同一天生日的概率是多少。

以下是代码的主要功能和步骤：

生成随机生日：getBirthdays 函数会生成指定数量的随机生日，这些生日都在2001年。
寻找匹配的生日：getMatch 函数检查生成的生日列表中是否有重复的生日，如果有，就返回第一个匹配的生日。
用户交互：代码首先询问用户要生成多少个生日（最多100个），然后显示这些生日。
单次模拟：代码会检查当前生成的生日列表中是否有匹配的生日，并打印结果。
多次模拟：代码会进行100,000次模拟，每次模拟都会生成相同数量的生日，并检查是否有匹配的生日。最后，计算在这100,000次模拟中，至少有一次匹配的生日的概率。

代码确实有些地方可以简化

以下是一些建议：

getMatch 函数可以简化，因为如果列表中有重复的生日，使用集合（set）会更高效。
代码中有重复的部分，比如两次进行100,000次模拟的循环，这些可以合并或重构。
代码中的用户交互和打印输出可以更加清晰和简洁。

以下是对代码的一些简化建议：

import datetime, random
def getBirthdays(numberOfBirthdays):
    startOfYear = datetime.date(2001, 1, 1)
    return [startOfYear + datetime.timedelta(days=random.randint(0, 364)) for _ in range(numberOfBirthdays)]
def hasMatchingBirthday(birthdays):
    return len(birthdays) != len(set(birthdays))
MONTHS = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
numBDays = 0
while True:
    print('How many birthdays shall I generate? (Max 100)')
    response = input('> ')
    if response.isdecimal() and (0 < int(response) <= 100):
        numBDays = int(response)
        break
print(f'Here are {numBDays} birthdays:')
birthdays = getBirthdays(numBDays)
print(', '.join(f'{MONTHS[birthday.month-1]} {birthday.day}' for birthday in birthdays))
if hasMatchingBirthday(birthdays):
    print('In this simulation, multiple people have the same birthday.')
else:
    print('In this simulation, there are no matching birthdays.')
print(f'Generating {numBDays} random birthdays 100,000 times...')
input('Press Enter to begin...')
simMatch = sum(hasMatchingBirthday(getBirthdays(numBDays)) for _ in range(100_000))
probability = round(simMatch / 100_000 * 100, 2)
print(f'Out of 100,000 simulations of {numBDays} people, there was a matching birthday in that group {simMatch} times.')
print(f'This means that {numBDays} people have a {probability}% chance of having a matching birthday in their group.')

这个简化版本去除了不必要的重复代码，并使逻辑更加清晰。

回页目录

3、“生日悖论”的前世今生

“生日悖论”_{（Birthday Paradox）}是一个概率论中的问题，它描述了在一个随机选取的群体中，至少有两个人共享相同生日的概率比直觉上要高得多。

以下是关于“生日悖论”的前世今生：

3.1 前世

起源

“生日悖论”并没有一个确切的起源点，因为它基于的概率原理在数学和统计学中早已存在。然而，这个问题通常被认为是在20世纪中叶开始广泛传播的。

数学原理

生日悖论背后的数学原理是基于“鸽巢原理”（也称为狄利克雷抽屉原理），这个原理简单地说就是如果有n个抽屉和n+1个物品，那么至少有一个抽屉里将包含不止一个物品。在生日悖论中，抽屉可以看作是365天（不考虑闰年），而物品则是人的生日。

回页目录

3.2 今生

定义

生日悖论的经典问题是：在一个房间里至少需要多少人，才能使得至少有两个人有相同生日的概率超过50%？

解答

直觉上，许多人会认为这个数字会很大，但实际上，只需要23个人，这个概率就会超过50%。这是因为随着人数的增加，不共享生日的概率迅速下降。

计算方法

计算至少两个人共享生日的概率的一种方法是计算所有人都有不同生日的概率，然后用1减去这个概率。

假设有n个人，那么第一个人可以选择任意一天生日，第二个人不能选择第一个人的生日，所以有364种选择，依此类推。

因此，所有人都有不同生日的概率是：

$\frac{365}{365}\times \frac{364}{365} \times \frac{363}{365} \times \ldots \times \frac{365 - n + 1}{365}$
当n = 23时，这个概率约为0.4927，所以至少两个人共享生日的概率是 $1 - 0.4927 = 0.5073$ ，即50.73%。

生日悖论，是指在一定数量的人中，至少有两个人生日相同的概率远大于直觉判断的现象。其计算公式可以用来估算在多少人中至少有两个人生日相同的概率。

如果假设一年有365天_{（不考虑闰年）}，并且每个人的生日是任何一天都是可能的，那么在n个人中至少有两个人生日相同的概率 $P$ 可以用以下公式来计算：

$\frac{365 \times 364 \times 365 \times \ldots \times (365 - n + 1)}{365^n}$

这里的计算方式是先计算出所有人都有不同生日的概率，然后用1减去这个概率得到至少有两个人生日相同的概率。

更一般化的公式是：

$\frac{365!}{(365 - n)! \times 365^n}$

但是，由于阶乘计算在n稍大时非常不实用，通常我们会使用以下近似公式：

$\approx 1 - e^{-n(n - 1)/(2 \times 365)}$
或者 $\approx 1 - e^{\frac{-n(n - 1)}{2 \times 365}}$

这里的e是自然对数的底数_{（大约等于2.71828）}。

在实际应用中，当n的值不是很大时，通常使用下面的简化公式来进行计算：

$\approx 1 - \left(1 - \frac{1}{365}\right)^{n \times (n - 1)/2}$
或者 $\approx 1 - \left(1 - \frac{1}{365}\right)^{\frac{n \times (n - 1)}{2}}$

这个公式是基于组合的概念，假设每对人的生日都不相同，然后用1减去这个概率得到至少有一对人生日相同的概率。这个公式在n较小时相当准确，但在n较大时，误差会稍微增加。

实际应用

生日悖论不仅在数学教育中是一个常用的例子，它还在密码学和其他领域中有实际应用。例如，它说明了为什么简单的密码很容易被破解：如果密码是随机生成的，那么只需要尝试相对较少的密码组合，就有很高的概率找到正确的密码。

扩展和变体

生日悖论也有许多扩展和变体，例如考虑闰年、考虑不同的国家或文化背景下的生日分布，或者研究不同的概率模型。

3.3 结论

生日悖论之所以被称为“悖论”，是因为它的结果与我们的直觉相悖。它提醒我们，**概率和直觉并不总是一致的**，而且在进行概率计算时，我们需要依赖数学而不是直觉。这个简单的概率问题在数学教育中起到了重要作用，并且它在现实世界的应用中也展示了其重要性。

回页目录

4、我的“生日悖论”

通过我的ai学习搭子的帮助，我认真仔细地学习了“生日悖论”相关知识点。依我一贯的python思维，代码化了通用计算公式；亦用python代码完成了模拟。但代码未经“打磨”，比较粗糙。😉

4.1 公式计算

Python代码


# 阶乘计算 #
def birthdayFormulaCalculator(n: int, year: int) -> float:
    ''' “生日悖论”公式计算器，参数n为生日个数 '''
    yearday = getYearday(year) # 获取闰年或者平年天数
    fractor = 1 # 阶乘结果
    deltaday = yearday
    for i in range(n):
        fractor *= deltaday
        deltaday -= 1
        
    return 1 - fractor / yearday**n # 返回共享生日的概率


# 分项计算 #
def birthdayFormulaCalculator(n: int, year: int) -> float:
    ''' “生日悖论”公式计算器，参数n为生日个数 '''
    yearday = getYearday(year) # 获取闰年或者平年天数
    rate = 1 # 生日不同的概率
    deltaday = yearday
    for i in range(n):
        rate *= deltaday / yearday
        deltaday -= 1
        
    return 1 - rate # 返回共享生日的概率
    
#input(birthdayFormulaCalculator(23, 2025)) # 函数验证用语句

回页目录

4.2 代码模拟

我的模拟代码

#!sur/bin/nve python
# coding: utf-8
from random import randint # 随机取整方法加载
from datetime import datetime # 日期时间运算方法加载
from datetime import timedelta # 


def tipRunning():
    ''' “程序正在运算……”提示函数 '''
    from time import time # 一般在脚本最前面加载工具。在这再写一次，是防止调用脚本没加载本函数所有工具
    k = int(str(time()) -2: )%27
    print(' '*40, end='\r')
    print(f"{' '*k}{'程序正在运算……'}", end='\r')


def getYearday(year: str) -> int:
    ''' 返回yrar参数年份总天数 '''
    leapyear = lambda year: True if (not year%4 and not not year%100) or not year%400 else False # 三元操作语句闰年判定
    return 366 if leapyear(int(year)) else 365 # 闰年366，平年355

#print(getYearday('2024')) # 验证函数用语句
#input(getYearday('2023')) # 验证函数用语句


def strShareBirthday(year:int, birthdays: list, ) -> str:
    ''' 字符串格式化共享生日 '''
    MONTHS = 'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'
    for i in birthdays:
        if birthdays.count(i) > 1:
            shareBirthday = timedelta(days=i)
            break # 找到随机生日列表中的第一个共享生日，结束遍历
    
    firstDay = datetime(year, 1, 1) # 实例化参数年份1月1号为datetime对象
    shareBirthday = firstDay + shareBirthday
    month = shareBirthday.month
    #print(month) # 调试用语句
    month = MONTHS month-1 
    day = shareBirthday.day
    print(f"\n\n{f' 共享生日：{year:0>4} {month} {day:0>2} ':.^37}\n\n")

#input(strShareBirthday(2024,  317, 317 )) # 函数试炼语句


def isSameBirthday(n: int, year: str, days: int, k=0) -> bool:
    ''' 判定在参数n个随机生日中，是否有共享生日，默认打印共享生日关闭 '''
    birthdays =  randint(0, getYearday(year)-1) for i in range(n)  # 随机选择n个生日，范围一年第一天到最后一天
    #print(birthdays) # 程序调试用语句

    if len(birthdays) == len(set(birthdays)):
        return True # 无相同生日返回真值
    
    if k: # 打印开关默认关闭
        strShareBirthday(year, birthdays) # 打印共享生日
    else:
        tipRunning() # 打印程序正在运算文本提示

#input(isSameBirthday(12, 2024, 365)) # 调试用语句


# 解析式模拟 #
def birthdayParadox(n: int, year: int, days: int, times=100_000) -> float:
    ''' 代码模拟“生日悖论”，默认100_000次 '''
    input(f"\n\n按任意键进行{times:0>2}次模拟随机{n:0>2}个生日操作：\n\n")
    rate = sum( 1 if isSameBirthday(n, year, days) else 0 for i in range(times) ) / times # 10_000次模拟无共享生日概率
    print(f"{' '*42}", end='\r')
    print(f"\n\n{f' {times}次模拟随机{n}个生日 ':.^34}\n\n{f'共享生日概率：{(1 - rate)*100:.2f}%':^38}\n\n")



# for循环模拟 #
def birthdayParadox(n: int, year: int, days: int, times=100_000) -> float:
    ''' 代码模拟“生日悖论”，默认100_000次 '''
    input(f"\n\n按任意键进行{times:0>2}次模拟随机{n:0>2}个生日操作：\n\n")
    rate = 0
    for i in range(times):
        rate += 1 if isSameBirthday(n, year, days) else 0 
        
    rate /= times
    print(f"{' '*42}", end='\r')
    print(f"\n\n{f' {times}次模拟随机{n}个生日 ':.^34}\n\n{f'共享生日概率：{(1 - rate)*100:.2f}%':^38}\n\n")


def countBirthdayParadox(n: int, year: int, days: int) -> None:
    ''' 1到30代码模拟操作 '''
    for i in range(1, 31):
        input(f"\n\n按任意键进行{i:0>2}次模拟随机{n:0>2}个生日操作：\n\n")
        count = 0
        for j in range(i):
            if isSameBirthday(n, year, days, k=1): # 打印共享生日参数调用函数
                count += 1
                
        input(f"共享生日概率：{(1-count/i)*100:.2f}%\n\n{'':=^42}\n")


def main() -> None:
    tip = f"\n\n{' 生日悖论模拟 ':=^36}\n\n输入生日年份和生日数量\n(2~100)，如：2024 23\n\n{'':>11}$ "

    try:
        year, n = map(int, input(tip).strip().split())
    except:
        raise ValueError('输入字符类型错误！')
    if n < 2 or n > 100:
        raise ValueError('模拟生日个数范围错误！')
    elif year < 1000 or year > 9999:
        raise ValueError('年份输入错误！')
        
    days = getYearday(year)
    countBirthdayParadox(n, year, days) # 模拟1-30次

    print("\n") # 打印空行
    birthdayParadox(n, year, days) # 缺省times，默认100_000次
    print(f"\n\n{'':=^42}\n\n")


if __name__ == '__main__':
    
    try:
        main() # 执行主函数
    except ValueError as error:
        print(f"\n\n{'':.^42}\n\n{'':>8}错误类型：{error}\n\n{'':.^42}\n\n")

4.3 ai点评

恳请ai点评代码

ai回复

您的Python脚本用于模拟“生日悖论”，整体上写得相当不错，以下是一些点评和建议：

优点：

代码结构清晰：您将不同的功能模块化，定义了多个函数来处理不同的任务，这有助于代码的维护和重用。
注释丰富：您在代码中添加了详细的注释，这有助于其他开发者理解代码的意图和功能。
异常处理：您在主函数中使用了try-except结构来捕获和处理潜在的错误，这提高了脚本的健壮性。

建议：

代码重复：您在birthdayParadox函数中定义了两次，可以考虑合并或者使用不同的函数名来区分。
变量命名：变量命名应更具描述性，例如k在isSameBirthday函数中不是很清楚它的作用，可以改为print_share等更具描述性的名称。
性能优化：在isSameBirthday函数中，您使用了列表推导式来生成生日列表，这可能会在大量模拟时消耗较多内存。可以考虑使用生成器表达式。
代码风格：Python中通常推荐使用4个空格进行缩进，而不是tab字符，以保持代码风格的一致性。
字符串格式化：在strShareBirthday函数中，month = MONTHS month-1这一行有语法错误，应该使用索引访问。
函数参数：getYearday函数的参数名为year，但在类型注解中使用了str，这可能会造成混淆。建议统一类型。
输入函数的使用：在countBirthdayParadox函数中，使用input函数来显示信息并不合适，因为它会等待用户输入。应该使用print函数。
以下是一些具体的代码修正示例：

def strShareBirthday(year: int, birthdays: list) -> str:
    MONTHS = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
    # ... 其他代码不变
    month = MONTHS[shareBirthday.month - 1]  # 修正这里的语法错误
    # ... 其他代码不变

def isSameBirthday(n: int, year: int, days: int, k=0) -> bool:
    # ... 其他代码不变
    birthdays = (randint(0, days - 1) for i in range(n))  # 使用生成器表达式
    # ... 其他代码不变

总的来说，您的脚本已经很好地实现了“生日悖论”的模拟，只需进行一些细节上的调整和优化。继续加油！

回页目录

5、与ai学习搭子探讨优化

在ai学习搭子的帮助下，进行了代码优化，去除冗余代码、“重复”代码，合并函数。设置函数参数“开头”，其法一就是用if-else、合并“同质同效”函数，用参数“开关”控制代码执行。

5.1 优化代码

#!sur/bin/nve python
# coding: utf-8
from time import time # 秒时间(时间截)
from random import randint # 随机取整
from datetime import datetime # 日期时间对象运算
from datetime import timedelta # 时间差值对象


def runningTip() -> None:
    ''' “程序正在运算……”提示函数 '''
    # 本函数要用到time.time，请确保以from  time import time的形式载入或者以time = time.time的形式别名
    k = str(time()).split('.')[1][2:] # 取秒时间数字串小数部分第二个字符以后的字符整数
    k = k if k else '0' # 当k为''空字符串时置0
    k = int(k) % 26 # 模26是确保“程序正在运算……”提示字符串能够在宽度为42个英文字符的行宽度随机位置打印
    print(' '*42, end='\r') # 清空行
    print(f"{' '*k}{'程序正在运算……'}", end='\r') # 前插0~26个英文空格不换行打印


def getYearday(year: int) -> int:
    ''' 返回yrar参数年份总天数 '''
    leapyear = True if (not year%4 and not not year%100) or not year%400 else False # 三元操作语句判闰年
    return 366 if leapyear else 365 # 返回闰年366天，平年365天


def birthdayFormulaCalculator(n: int, year: int, k=1) -> float:
    ''' “生日悖论”公式计算器，参数n为生日个数，默认“分项式计算”，year为模拟生日年份 '''
    yearday = getYearday(year) # 获取闰年或者平年天数
    
    if k: # 分项计算 # 默认。模拟生日人数较大时更适宜
        rate = 1 # 生日不同的概率
        deltaday = yearday
        for i in range(n):
            rate *= deltaday / yearday
            deltaday -= 1
        
        return 1 - rate # 返回共享生日的概率
    
    # 阶乘计算 # 模拟生日人数较小时效率更高。。不用if-else形式，是为代码编排少一组缩进，此写法同质同效
    fractor = 1 # 阶乘结果变量初值
    deltaday = yearday
    for i in range(n):
        fractor *= deltaday
        deltaday -= 1
        
    return 1 - fractor / yearday**n # 返回共享生日的概率


def strShareBirthday(year:int, birthdays: list, ) -> str:
    ''' 字符串格式化共享生日：参数year为模拟年份，birthdays是随机生日列表 '''
    
    def strBirthday(year: int, shareBirthday: timedelta):
        ''' 字符串格式化“共享生日” '''
        MONTHS = 'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'
        firstDay = datetime(year, 1, 1) # 实例化参数年份1月1号为datetime对象
        shareBirthday = firstDay + shareBirthday
        month = shareBirthday.month
        month = MONTHS[month-1] # 转换月份为英文字符
        day = shareBirthday.day
        print(f"\n\n{f' 共享生日：{year:0>4} {month} {day:0>2} ':.^37}\n\n")

    for i in birthdays:
        if birthdays.count(i) > 1:
            shareBirthday = timedelta(days=i)
            strBirthday(year, shareBirthday) # 生日字符串格式打印
            break # 只需找到第一组共享生日。是在必有共享生日分支调用


def isSameBirthday(n: int, year: int, days: int, k=0) -> bool:
    ''' 判定在参数n个随机生日中，是否有共享生日，默认打印共享生日关闭 '''
    birthdays = [randint(0, getYearday(year)-1) for i in range(n)] # 随机选择n个生日，范围一年第一天到最后一天

    if len(birthdays) == len(set(birthdays)):
        return True # 无相同生日返回真值
    
    if k: # 打印开关默认关闭
        strShareBirthday(year, birthdays) # 打印共享生日
    else:
        runningTip() # 打印程序正在运算文本提示


def birthdayParadox(n: int, year: int, days: int, times=100_000, k=1) -> float:
    ''' 代码模拟“生日悖论”，默认100_000次 '''
    input(f"{'':=^42}\n\n按任意键进行{times:0>2}次模拟随机{n:0>2}个生日操作：\n{'':.^42}\n")
    
    if k: # 解析式模拟 # 默认。模拟人数较小时效率更高
        rate = sum([1 if isSameBirthday(n, year, days) else 0 for i in range(times)]) / times # 10_000次模拟无共享生日概率
        print(f"{' '*42}", end='\r')
        print(f"\n\n{f' {times}次模拟随机{n}个生日 ':.^34}\n\n{f'共享生日概率：{(1 - rate)*100:.2f}%':^35}\n\n")
    else:
        # for循环模拟 # 模拟人数较大时更适宜。不用if-else形式，是为代码编排少一组缩进，此写法同质同效
        rate = 0
        for i in range(times):
            rate += 1 if isSameBirthday(n, year, days) else 0 
        
        rate /= times
        print(f"{' '*42}", end='\r')
        print(f"\n\n{f' {times}次模拟随机{n}个生日 ':.^34}\n\n{f'共享生日概率：{(1 - rate)*100:.2f}%':^38}\n\n")


def countBirthdayParadox(n: int, year: int, days: int) -> None:
    ''' 1到30代码模拟操作 '''
    # 专列一个模块，是为“干净”main函数代码。这里以打印共享生日的方式调用isSameBirthday #
    for i in range(1, 31):
        input(f"\n\n按任意键进行{i:0>2}次模拟随机{n:0>2}个生日操作：\n\n")
        count = 0
        for j in range(i):
            if isSameBirthday(n, year, days, k=1): # 打印共享生日参数调用函数
                count += 1
                
        input(f"共享生日概率：{(1-count/i)*100:.2f}%\n\n{'':=^42}\n")


def main() -> None:
    ''' 主操作模块 '''
    # 虽然countBirthdayParadox与birthdayParadox，一般来说不必共存。但前者是后者的“批发”操作，所以予以保留 #
    tip = f"\n\n{' 生日悖论模拟 ':=^36}\n\n输入生日年份和生日数量\n(2~100)，如：2024 23\n\n{'':>11}$ "

    try: # 输入及数据预处理 #
        year, n = map(int, input(tip).strip().split())
    except ValueError:
        raise ValueError('输入字符类型错误！')

    if n < 2 or n > 100:
        raise ValueError('模拟生日个数范围错误！')
    elif year < 1000 or year > 9999:
        raise ValueError('年份输入错误！')
        
    days = getYearday(year)

    # 运算部分 #
    print(f"\n\n{f' 阶乘公式计算 ':.^36}\n\n")
    for i in range(2, 31):
        print(f"随机生日人数：{i:0>2}，共享生日概率： {100*birthdayFormulaCalculator(i, year, k=0):.2f}%") # 以阶乘计算的方式调用“生日悖论计算器”
    input(f"\n\n{f' 以上是模拟2~30个随机生日的公式计算 ':.^27}\n\n")

    #countBirthdayParadox(n, year, days) # 调用模块，模拟1-30次“生日悖论”

    print("\n") # 打印空行
    birthdayParadox(n, year, days, k=0) # 缺省times，默认100_000次，for循环方式计算
    print(f"\n\n{'':=^42}\n\n")


if __name__ == '__main__':
    
    try:
        main() # 执行主函数
    except ValueError as error:
        print(f"\n\n{'':.^42}\n\n{'':>8}错误类型：{error}\n\n{'':.^42}\n\n")

回页目录

5.2 ai点评

代码点评

您的代码是一个用于模拟“生日悖论”的程序，整体结构清晰，功能明确。

以下是一些具体的点评：

函数定义：您定义了多个函数，每个函数都有明确的职责，这是非常好的编程习惯。例如，getYearday 函数用于计算年份的总天数，isSameBirthday 函数用于判断是否有共享生日。
代码注释：代码中包含了许多注释，这有助于理解每个函数和代码块的作用。建议在注释中说明更多的细节，例如参数的意义、函数的返回值等。
错误处理：您在主函数中使用了 try-except 结构来处理输入错误，这是一个很好的实践。建议在处理错误时提供更详细的错误信息，帮助用户理解如何解决问题。
代码风格：整体代码风格良好，变量命名清晰。但在某些地方，例如打印语句中的格式化字符串，可以进一步简化以提高可读性。
性能考虑：在 birthdayParadox 函数中，您使用了列表推导式来计算共享生日的概率。这是一种高效的方法。但在 countBirthdayParadox 函数中，您使用了两个嵌套的循环，这可能会影响程序的运行速度。可以考虑优化这部分代码。
功能实现：您的程序成功实现了生日悖论的模拟。但在 main 函数中，您首先执行了 countBirthdayParadox 函数，然后又执行了 birthdayParadox 函数。这两个函数的功能有部分重叠，可以考虑合并以提高代码的效率。

特色和不足

整体结构清晰，模块化设计合理，易于阅读和维护。
注释详细，有助于理解代码功能和各部分的作用。
异常处理得当，能够有效捕获并处理输入错误。
使用了Python的高级特性，如列表推导式、生成器表达式等，提高了代码的简洁性和可读性。
在某些地方，代码可以进行优化。例如，getYearday函数可以简化，isSameBirthday函数中的k参数默认值设置为0，但在调用时又设置为1，这种不一致可能导致理解上的困惑。

回页目录

5.3 代码文档

代码文档：生日悖论模拟程序

一、概述
本程序旨在模拟“生日悖论”现象，通过计算和模拟随机生日，验证在一定人数范围内，至少有两人生日相同的概率。

二、功能模块

runningTip：显示程序正在运行的提示信息。
getYearday：根据年份判断是平年还是闰年，并返回该年的总天数。
birthdayFormulaCalculator：根据生日悖论公式计算共享生日的概率。
strShareBirthday：格式化输出共享生日的日期。
isSameBirthday：判断随机生成的生日列表中是否存在共享生日。参数 n 为生日数量，year 为年份，days 为该年的总天数。参数 k 用于控制是否打印共享生日，默认为 0_{（不打印）}。
birthdayParadox：模拟生日悖论，计算共享生日的概率。参数 n 为生日数量，year 为年份，days 为该年的总天数，times 为模拟次数，k 用于控制是否使用解析式模拟，默认为 1_{（使用解析式模拟）}。
countBirthdayParadox：模拟1到30次生日悖论，输出共享生日的概率。
main：主函数，负责程序流程控制和用户交互。用于接收用户输入并执行生日悖论的模拟。

三、使用说明

运行程序后，根据提示输入生日年份和生日数量（2~100）。
程序将自动计算并输出2到30个随机生日的共享生日概率。
程序默认进行100,000次模拟，计算给定人数的共享生日概率。

四、注意事项

输入年份时，请确保年份在1000到9999之间。
输入生日数量时，请确保数量在2到100之间。

五、异常处理

输入字符类型错误：程序将提示“输入字符类型错误！”并退出。
年份输入错误：程序将提示“年份输入错误！”并退出。
模拟生日个数范围错误：程序将提示“模拟生日个数范围错误！”并退出。

使用方法：
运行程序后，根据提示输入年份和生日数量（2~100），程序将执行模拟并打印结果。

注意事项：

输入的年份应在 1000 到 9999 之间。
输入的生日数量应在 2 到 100 之间。

回页目录

5.4 代码运行效果截屏图片

-代码运行效果截屏图片
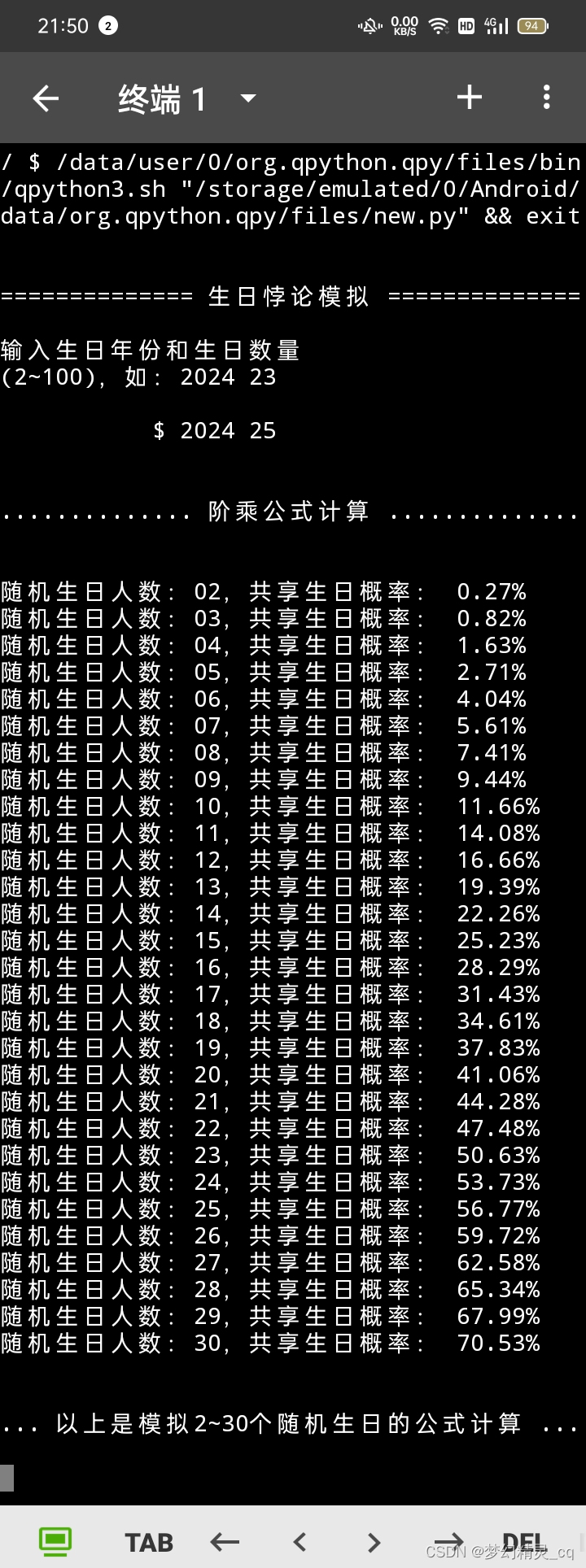
在这里插入图片描述
公式计算

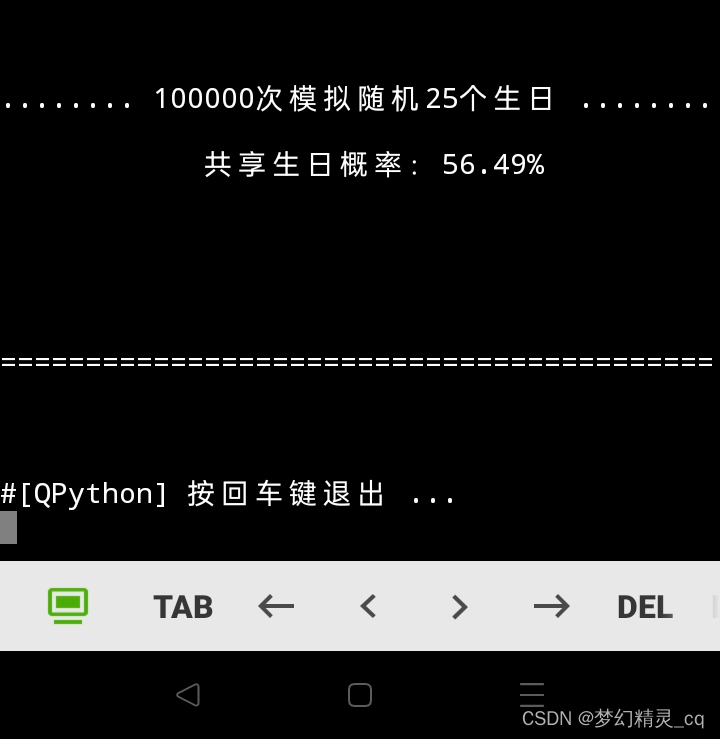
10w次模拟

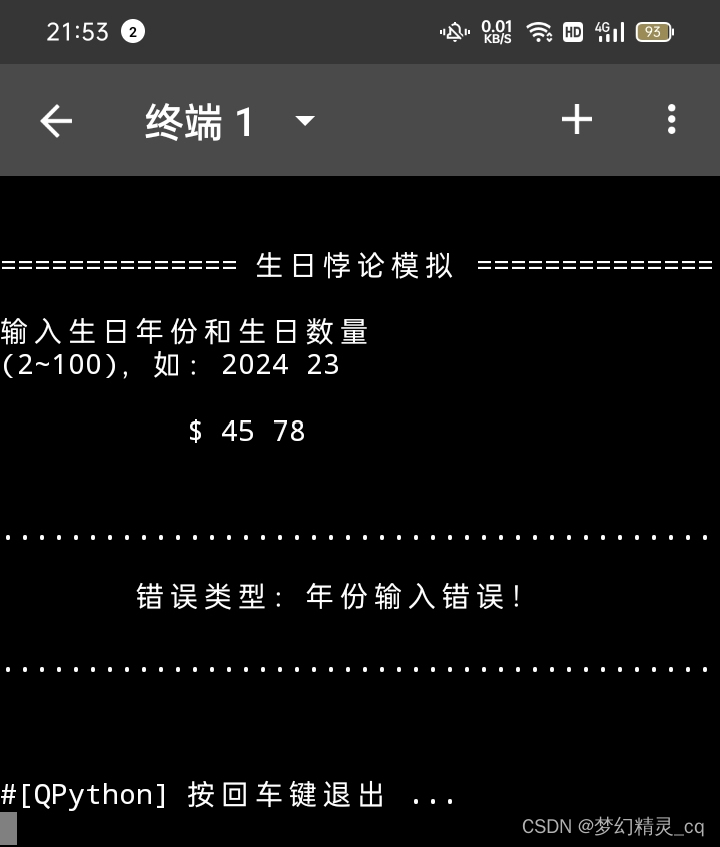
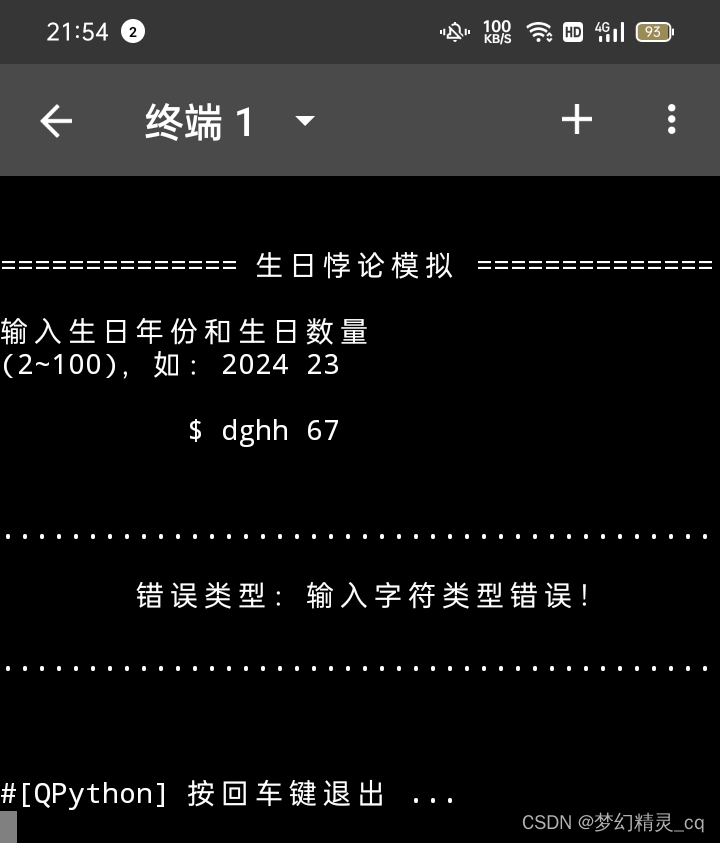
错误提示

1~30次模拟

回页目录

6、感悟

自码的代码也像原石，虽“肚里有货”₍₎，也要精雕细琢，才可以逐渐温润光洁，让人赏心悦目。

回页首

上一篇：简析“请求头”_{(请求头是HTTP请求的重要部分，可以用“头部字典”按需定制请求头)}
下一篇：

我的HOT博：

本次共计收集 311 篇博文笔记信息，总阅读量43.82w。数据于2024年03月22日 00:50:22完成采集，用时6分2.71秒。阅读量不小于6.00k的有 $7$ 篇。

001
标题：让QQ群昵称色变的神奇代码
_{(浏览阅读 5.9w )}
地址：https://blog.csdn.net/m0_57158496/article/details/122566500
点赞：25 收藏：86 评论：17
摘要：让QQ昵称色变的神奇代码。
首发：2022-01-18 19:15:08
最后编辑：2022-01-20 07:56:47
002
标题：Python列表(list)反序(降序)的7种实现方式
_{(浏览阅读 1.1w )}
地址：https://blog.csdn.net/m0_57158496/article/details/128271700
点赞：8 收藏：35 评论：8
摘要：Python列表(list)反序(降序)的实现方式：原址反序，list.reverse()、list.sort()；遍历，全数组遍历、1/2数组遍历；新生成列表，resersed()、sorted()、负步长切片[::-1]。
首发：2022-12-11 23:54:15
最后编辑：2023-03-20 18:13:55
003
标题：pandas 数据类型之 DataFrame
_{(浏览阅读 9.7k )}
地址：https://blog.csdn.net/m0_57158496/article/details/124525814
点赞：7 收藏：36
摘要：pandas 数据类型之 DataFrame_panda dataframe。
首发：2022-05-01 13:20:17
最后编辑：2022-05-08 08:46:13
004
标题：个人信息提取(字符串)
_{(浏览阅读 8.2k )}
地址：https://blog.csdn.net/m0_57158496/article/details/124244618
点赞：2 收藏：15
摘要：个人信息提取(字符串)_个人信息提取python。
首发：2022-04-18 11:07:12
最后编辑：2022-04-20 13:17:54
005
标题：Python字符串居中显示
_{(浏览阅读 7.6k )}
地址：https://blog.csdn.net/m0_57158496/article/details/122163023
评论：1
006
标题：罗马数字转换器|罗马数字生成器
_{(浏览阅读 7.5k )}
地址：https://blog.csdn.net/m0_57158496/article/details/122592047
摘要：罗马数字转换器|生成器。
首发：2022-01-19 23:26:42
最后编辑：2022-01-21 18:37:46
007
标题：回车符、换行符和回车换行符
_{(浏览阅读 6.0k )}
地址：https://blog.csdn.net/m0_57158496/article/details/123109488
点赞：2 收藏：3
摘要：回车符、换行符和回车换行符_命令行回车符。
首发：2022-02-24 13:10:02
最后编辑：2022-02-25 20:07:40