WPF+Mvvm 项目入门完整教程（一）

news2024/11/13 9:20:18

WPF+Mvvm 入门完整教程一

  • 创建项目
    • MvvmLight框架安装
    • 完善整个项目的目录结构
    • 创建自定义的字体资源
    • 下载更新和使用字体资源

创建项目

	打开VS2022,点击创建新项目,选择**WPF应用（.NET Framework）** 创建一个名称为 CommonProject_DeskTop 的项目，如下图所示：

在这里插入图片描述
在这里插入图片描述

MvvmLight框架安装

点击项目解决方案，右键管理Nuget程序包管理，点击浏览，输入MvvmLight，找到框架程序集后点击安装。如下图所示：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
接受更改，等待安装完成后项目文件层级如下图所示，自动增加了一个ViewModel 的文件夹。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1936101.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++基础语法:STL之容器(5)--序列容器中的list(二)

C++基础语法:STL之容器(5)--序列容器中的list(二)

前言 "打牢基础,万事不愁" .C的基础语法的学习 引入 序列容器的学习.以<C Prime Plus> 6th Edition(以下称"本书")内容理解 本书中容器内容不多只有几页.最好是有数据结构方面的知识积累,如果没有在学的同时补上 接上一篇C基础语法:STL之容器…
阅读更多...
自己用vps起网页（用于测试题目回显）

自己用vps起网页（用于测试题目回显）

0x01 首先要有一台vps&#xff0c;这里我推荐dk盾 base64 UVGkGjcyNzA3NzA1NQ0x02 那么我们就可以进行环境的配置了 我是选择的nginx&#xff0c;因为挺好用的吧&#xff0c;各方面参数也还行 我是使用的Ubuntu 的vps所以下面的命令也只有Ubuntu可以使用sudo apt updatesu…
阅读更多...
＜Rust＞egui部件学习：如何在egui窗口中添加按钮button以及标签label部件？

＜Rust＞egui部件学习：如何在egui窗口中添加按钮button以及标签label部件？

前言 本专栏是关于Rust的GUI库egui的部件讲解及应用实例分析&#xff0c;主要讲解egui的源代码、部件属性、如何应用。 环境配置 系统&#xff1a;windows 平台&#xff1a;visual studio code 语言&#xff1a;rust 库&#xff1a;egui、eframe 概述 本文是本专栏的第二篇博…
阅读更多...
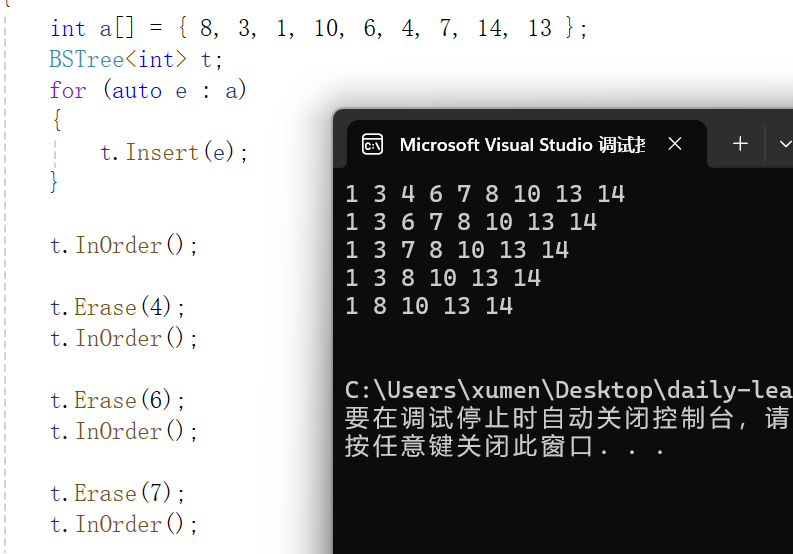
15. 【C++】详解搜索二叉树 | KV模型

15. 【C++】详解搜索二叉树 | KV模型

目录 1.定义 初始化 插入 查找 删除 完整代码 2.运用 K 模型和 KV 模型详解 K 模型 KV 模型 代码解释 为了更好地理解 map 和 set 的特性&#xff0c;和后面讲解查找效率极高的平衡搜索二叉树&#xff0c;和红黑树去实现模拟&#xff0c;所以决定在这里对搜索二叉树…
阅读更多...
基于asp.net小区物业信息管理系统设计与实现

基于asp.net小区物业信息管理系统设计与实现

博主介绍&#xff1a;专注于Java .net php phython 小程序 等诸多技术领域和毕业项目实战、企业信息化系统建设&#xff0c;从业十五余年开发设计教学工作 ☆☆☆ 精彩专栏推荐订阅☆☆☆☆☆不然下次找不到哟 我的博客空间发布了1000毕设题目 方便大家学习使用 感兴趣的可以…
阅读更多...
【机器学习】使用Python的dlib库实现人脸识别技术

【机器学习】使用Python的dlib库实现人脸识别技术

&#x1f525; 个人主页&#xff1a;空白诗 文章目录 一、引言二、传统人脸识别技术1. 基于几何特征的方法2. 基于模板匹配的方法3. 基于统计学习的方法 三、深度学习在脸识别中的应用1. 卷积神经网络&#xff08;CNN&#xff09;2. FaceNet和ArcFace 四、使用Python和dlib库实…
阅读更多...
辅助类BigDecima/BigInteger

辅助类BigDecima/BigInteger

** 大数据的运算** 编号1方法解释1add2subtract-3multiply*4divide/
阅读更多...
p19 C语言操作符详解

p19 C语言操作符详解

算术操作符 1.除了%操作符之外&#xff0c;其他的几个操作符可以作用于整数和浮点数。 2.对于/操作符如果两个操作数都为整数&#xff0c;执行整数除法。而只要有浮点数值型的就是浮点除法。 3.%操作符的两个操作数必须为 整数。返回的是整除之后的余数。 #include<std…
阅读更多...
通信流程：https【SSL/TLS】，git仓库【https/SSH】，蓝牙【面对面快传/AirDrop】

通信流程：https【SSL/TLS】，git仓库【https/SSH】，蓝牙【面对面快传/AirDrop】

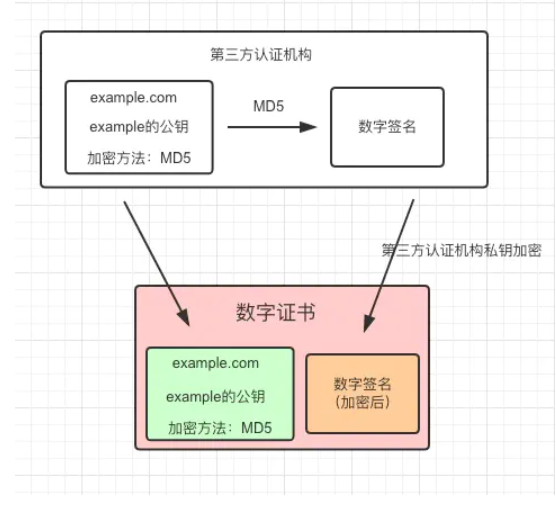
目录 HTTPS HTTP&#xff08;80端口&#xff09; SSL/TLS协议&#xff08;传输层&#xff0c;443端口&#xff09; 密文传输&#xff1a;SSL的后续版本TLS TLS1.2握手 1.摘要算法(散列函数 Hash Function)&#xff1a;验证信息的完整性&#xff0c;不可逆 第三方认证 引…
阅读更多...
GO：Socket编程

GO：Socket编程

目录 一、TCP/IP协议族和四层模型概述 1.1 互联网协议族&#xff08;TCP/IP&#xff09; 1.2 TCP/IP四层模型 1. 网络访问层&#xff08;Network Access Layer&#xff09; 2. 网络层&#xff08;Internet Layer&#xff09; 3. 传输层&#xff08;Transport Layer&#…
阅读更多...
kotlin compose 实现应用内多语言切换（不重新打开App）

kotlin compose 实现应用内多语言切换（不重新打开App）

1. 示例图 2.具体实现 如何实现上述示例，且不需要重新打开App ①自定义 MainApplication 实现 Application ，定义两个变量： class MainApplication : Application() { object GlobalDpData { var language: String = "" var defaultLanguage: Strin…
阅读更多...
你不是拖延，是没找对感觉！

你不是拖延，是没找对感觉！

在这个快节奏的时代&#xff0c;学习效率成为了我们每个人都渴望提升的关键能力。如何通过训练潜意识、深化知识印象、调整学习模式、找到适合自己的学习方法&#xff0c;以及利用倒计时硬逼法来提高执行力&#xff1f; 1. 训练潜意识&#xff1a;形成习惯 习惯的力量是巨大的…
阅读更多...
使用python的pillow库生成图像验证码

使用python的pillow库生成图像验证码

一、pillow库 Pillow库&#xff1a;是一个功能强大的Python图像处理库&#xff0c;它提供了丰富的图像处理功能&#xff0c;使得用户能够方便地使用Python对图像进行各种操作。 二、图像验证码的分析 首先需要一个图像&#xff0c;图像上需要绘制验证码&#xff0c;还需要任意多…
阅读更多...
博客最细 STM32CubeProgrammer 软件使用教程 二（学不会举报我）

博客最细 STM32CubeProgrammer 软件使用教程 二（学不会举报我）

前言&#xff1a;编写不易&#xff0c;仅供学习&#xff0c;参考&#xff0c;请勿转载 前言&#xff1a;本篇教程是 STM32CubeProgrammer 软件使用教程二&#xff0c;通过本篇你可以学习到&#xff0c;使用STM32CubeProgrammer读取 flash RAM&#xff0c;开启读写保护&#x…
阅读更多...
科普文：TaobaoVM信息收集

科普文：TaobaoVM信息收集

网上关于TaobaoVM的信息很少&#xff0c;只有一个简介&#xff0c;就没有其他信息。毕竟这是别人企业自己的jvm&#xff0c;不可能公开。 Taobao VM 由AliJVM团队发布。阿里&#xff0c;国内使用Java最强大的公司&#xff0c;覆盖云计算、金融、物流、电商等众多领域&#xf…
阅读更多...
Python和C++行人轨迹预推算和空间机器人多传感融合双图算法模型

Python和C++行人轨迹预推算和空间机器人多传感融合双图算法模型

&#x1f3af;要点 &#x1f3af;双图神经网络模型&#xff1a;最大后验推理和线性纠错码解码器 | &#x1f3af;重复结构和过约束问题超图推理模型 | &#x1f3af;无向图模型变量概率计算、和积消息传播图结构计算、隐马尔可夫模型图结构计算、矩阵图结构计算、图结构学习 |…
阅读更多...
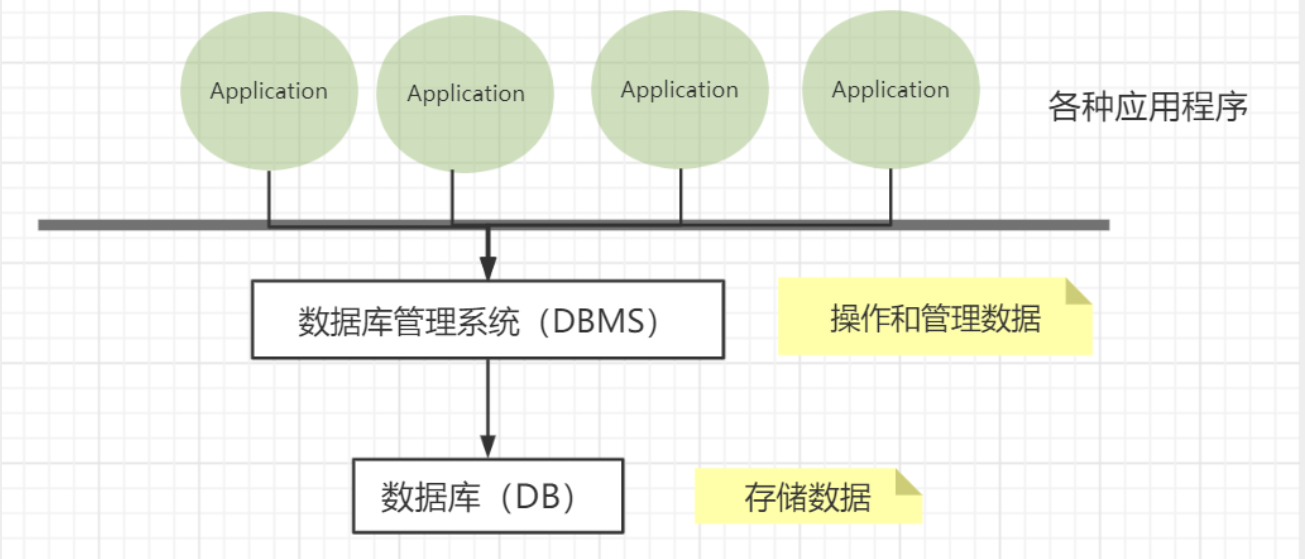
数据库MySQL学习第一天|了解数据库、数据类型、存储引擎、sql语言

数据库MySQL学习第一天|了解数据库、数据类型、存储引擎、sql语言

文章目录 了解数据库什么是数据库数据库分类MySQL概念 数据类型整数类型小数类型日期类型文本,二进制类型 存储引擎种类引擎选择 sql主键和外键主键设计原则选取策略 外键索引 表与表的关联在语法上关联关系sql约束sql注入聚合函数常见查询关键字 了解数据库 什么是数据库 概…
阅读更多...
网络安全协议系列

网络安全协议系列

目录 一、安全协议的引入 1.TCP/IP协议族中普通协议的安全缺陷 1.信息泄露 2.信息篡改 3.身份伪装 4.行为否认 2.网络安全需求 二、网络安全协议的定义 三、构建网络安全协议所需的组件 1.加密与解密 2.消息摘要 3.消息验证码 4.数字签名 5.密钥管理 1.建立共享…
阅读更多...
关于C#多个文本框输入的问题

关于C#多个文本框输入的问题

&#x1f3c6;本文收录于《CSDN问答解答》专栏&#xff0c;主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案&#xff0c;希望能够助你一臂之力&#xff0c;帮你早日登顶实现财富自由&#x1f680;&#xff1b;同时&#xff0c;欢迎大家关注&&收藏&…
阅读更多...
堆排序基本思想以及代码实现

堆排序基本思想以及代码实现

1、基本思想 堆排序是利用堆这种数据结构而设计的一种排序算法&#xff0c;堆排序是一种选择排序&#xff0c;它的最坏&#xff0c;最好&#xff0c;平均时间复杂度均为O(n*logn)&#xff0c;它也是不稳定排序。 堆是具有以下性质的完全二叉树&#xff1a;每个结点的值都大于或…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023