目录
- 一:杨氏矩阵
- 🐻何为杨氏矩阵?
- 🐻题目描述:
- 🐻思路一:
- 🐻思路二:
- 二:杨辉三角
- 🐻何为杨辉三角?
- 🐻题目描述:
- 🐻解题思路:
一:杨氏矩阵
🐻何为杨氏矩阵?
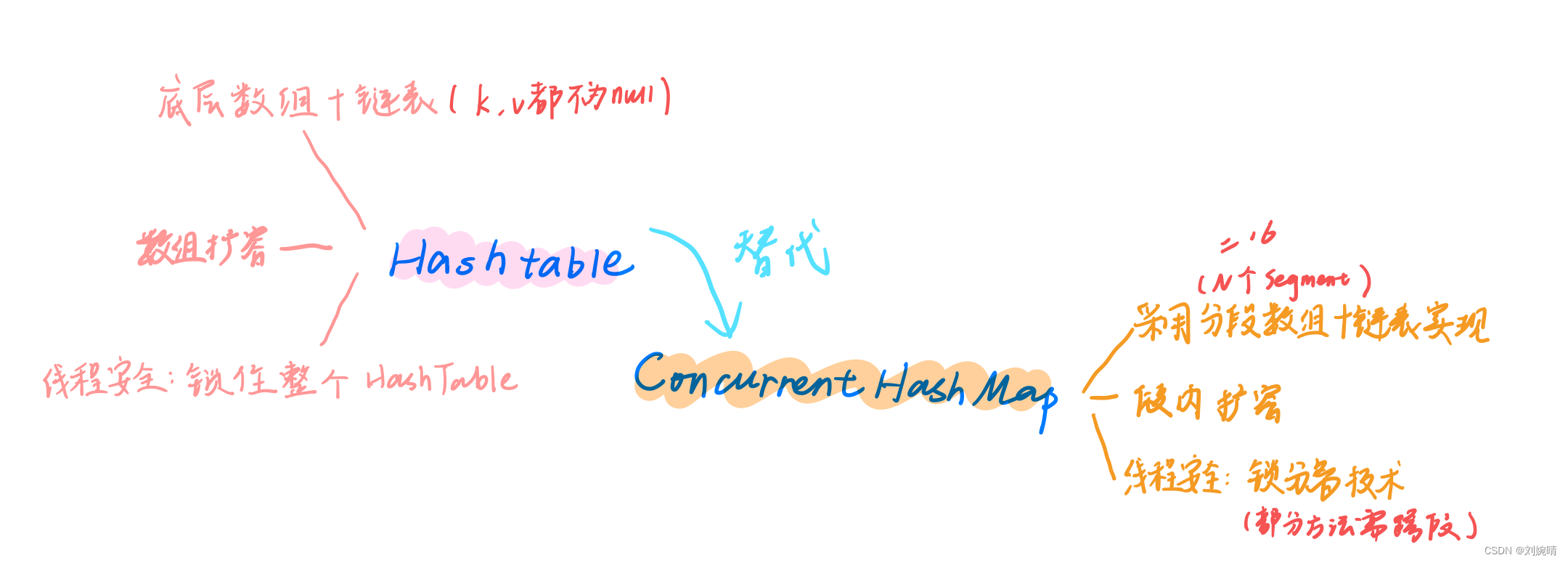
杨氏矩阵,是对组合表示理论和舒伯特演算很有用的工具。它提供了一种方便的方式来描述对称和一般线性群的群表示,并研究它们的性质。杨氏矩阵是剑桥大学大学数学家阿尔弗雷德·扬在1900年提出。然后在1903年,它被用于格奥尔格·弗罗贝纽斯的对称群研究中。它的理论得益于许多数学家的贡献得到进一步发展,包括珀西·麦克马洪,W.V.D.霍奇,G.deB.罗宾逊,吉安·卡咯罗塔,阿兰拉斯克斯,马塞尔·保罗斯库森博格和理查德·P·史丹利。
杨氏矩阵最显著的特点是: 矩阵的每一行从左到右是递增的,矩阵的每一列从上到下是递增的。

如上图就是一个杨氏矩阵。
🐻题目描述:
编写程序,在杨氏矩阵中查找某一数字是否存在,若存在打印出坐标,若不存在,打印 “没找到” 。要求:时间复杂度小于O(N)
🐻思路一:
关于杨氏矩阵我们很容易想到可以用一个二维数组来表示,现在问题就变成了在一个二维数组中查找一个数字,我们很容易想到的就是遍历整个二维数组,这种方法当然没问题,但是但是它的时间复杂度是O(N^2),不满足题目要求,因此需要换一种思路。
🐻思路二:
我们可以从杨氏矩阵的特点入手,来寻求解题方法。杨氏矩阵最显著的特点是: 矩阵的每一行从左到右是递增的,矩阵的每一列从上到下是递增的。因此我们不难发现:矩阵右上角的元素是第一行所有元素中最大的,同时也是最后一列所有元素中最小的。发现了这个特点以后,我们就可以让待查找的数字,与矩阵右上角的数字进行比较,如果待查找的数字比矩阵右上角的数字大,那待查找的数字就不可能在第一行,因为矩阵右上角的数字已经是第一行中最大的那个了,待查找的数字比矩阵右上角的数字还要大,此时就可以排除掉第一行的所有元素,在剩下的矩阵中查找。当待查找的数字比矩阵右上角的数字小的时候,那待查找的数字就不可能在矩阵的最后一列,因为矩阵右上角的数字已经是最后一列中最小的那个,待查找的数字比矩阵右上角的数字还要小,此时就可以排除掉矩阵最后一列的所有元素,在剩下的矩阵中查找。就一直这样让待查找的数字与矩阵右上角的数字作比较,最终就能比较出结果。分析的差不多了,接下来上代码。
void find_k(int arr[3][3], int r, int l, int k)
{
//右上角元素的坐标(x,y)
int x = 0;
int y = l - 1;
//定义一个标志变量flag
int flag = 0;
//找到时把flag置为1
//最终通过看flag的值来看是否找到
while (x < r && y >= 0)
{
if (arr[x][y] > k)//待查找的元素比右上角的元素小
//此时就可以排除掉最右边的一整列
{
y--;
}
else if (arr[x][y] < k)//待查找的元素比右上角的元素大
//此时就可以排除掉第一行所有元素
{
x++;
}
else//找到了
{
flag = 1;
printf("找到了,坐标是:%d %d\n", x, y);
break;//找到之后就要跳出循环
}
}
if (flag == 0)
{
printf("没找到");
}
}
int main()
{
int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };
int r = sizeof(arr)/sizeof(arr[0]);//r表示行
int l = sizeof(arr[0])/4;//l表示列
int k = 0;//k表示待查找的数字
printf("请输入要查找的数字:");
scanf("%d", &k);
find_k(arr, r, l, k);
return 0;
}
上面的代码已经满足题目要求,但是我们发现,查找结果是直接在find_k函数中打印出来的,如果我们想在主函数中打印查找结果该怎么办呢?判断找没找到很容易实现,如果找到了,就让find_k函数返回
1
1
1 ,如果没有找到,就让find_k函数返回
0
0
0 ,在主函数中用一个变量 ret 来接收函数的返回值,最终判断 ret 的大小就知道找没找到了。问题的难点在于:如果找到了,如何把坐标返回到主函数中,坐标是由两个数字组成的,因此无法直接利用 return 返回,还有什么办法呢?我们可以通过传地址来解决这个问题,观察find_k函数的参数,可以发现 r 和 l 很适合来做这个差事,把r 和 l 的地址传过去,如果找到了就把坐标存到r 和 l里面去。分析的差不多了,接下来上代码:
int find_k(int arr[3][3], int* pr, int* pl, int k)
{
//右上角元素的坐标(x,y)
int x = 0;
int y = *pl - 1;
while (x < *pr && y >= 0)
{
if (arr[x][y] > k)//待查找的元素比右上角的元素小
//此时就可以排除掉最右边的一整列
{
y--;
}
else if (arr[x][y] < k)//待查找的元素比右上角的元素大
//此时就可以排除掉第一行所有元素
{
x++;
}
else//找到了
{
*pr = x;
*pl = y;
return 1;//找到之后就返回1
}
}
return 0;
}
int main()
{
int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };
int r = sizeof(arr) / sizeof(arr[0]);//r表示行数
int l = sizeof(arr[0]) / 4;//l表示列数
int k = 0;//k表示待查找的数字
printf("请输入要查找的数字:");
scanf("%d", &k);
int ret = find_k(arr, &r, &l, k);
if (ret == 0)
{
printf("没找到\n");
}
else
{
printf("找到了,坐标是:%d %d\n", r, l);
}
return 0;
}
本题到这里就结束了。请看下一题,剧透以下:下个题也性杨哦
二:杨辉三角
🐻何为杨辉三角?
杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合

上图就是一个杨辉三角
🐻题目描述:
在屏幕上打印出杨辉三角
🐻解题思路:
首先应想到的是,利用二维数组来存储杨辉三角每一行的数值。接下来就该观察这些数值的特点了,不难发现二维数组的第
0
0
0 列和主对角线上的元素全是
1
1
1,对于这些位置上的元素我们可以直接把其初始化为
1
1
1 ,剩下位置上的元素是需要通过计算得到的,假设当前位置的下标是 i ,j,那么arr[i][j]的值就是其正上方和左上方的值的和,也就是公式:arr[i][j]=arr[i-1][j-1]+arr[i-1][j] 。其实从二维数组的第二行开始,主对角线上的元素也可以通过前面的公式计算得出,但此时必须保证公式中 arr[i-1][j] 的值是
0
0
0 ,如果当前的 arr[i][j] 是主对角线上的元素,那么 arr[i-1][j] 就不是杨辉三角中的一份子,但是为了计算出arr[i][j],我们必须保证arr[i-1][j]的值是
0
0
0 ,这一点也很容易实现,在定义二维数组的同时,我们只初始化数组的第一个元素,把它初始化为
1
1
1 ,此时数组中剩下的元素就会被默认初始化为
0
0
0 ,这样问题就得以解决了。二维数组中的数值处理完了,接下来就该把这个二维数组打印出来了,杨辉三角只占用了二维数组的左下角这一片区域,所以只需要打印出左下角这片区域的内容即可,这片区域的坐标特点是:列标小于等于行标。分析的差不多了,接下来上代码:
int main()
{
int arr[10][10] = {1};//直接把第一个元素初始化成1,也就是杨辉三角的第一行
int i = 0;
for (i = 1; i < 10; i++)//接下来从第二行开始
{
arr[i][0] = 1;//每行的第一列都没有区别,直接给1,保证不会越界
int j = 0;
for (j = 1; j <= i; j++)//从第二列开始
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
//打印
for (i = 0; i < 10; i++)
{
int j = 0;
for (j = 0; j <=i; j++)
{
//只需要打印左下区的元素
//左下区元素小标的特点是:列标小于等于行标
printf("%d ", arr[i][j]);
}
//一行打印结束换行
printf("\n");
}
return 0;
}
🎶结语:
今天分享了两道杨性题目,杨氏矩阵和杨辉三角,这两道题都是已二维数组为基础,再结合各自的特点最终完成题解,由此可见拿到题目最主要的就是发现题目的特点,结合特点去解题往往会达到事半功倍的效果。
今天的分享到这里就结束啦,以上的内容如果对你有帮助的话,可以动动小手点赞、评论、收藏,你的支持就是我前进路上最大的动力!