【深度学习】sdwebui的token_counter,update_token_counter,如何超出77个token的限制?对提示词加权的底层实现_prompt中token权重-CSDN博客文章浏览阅读1.6k次,点赞26次,收藏36次。文章探讨了如何在StableDiffusionProcessing中处理超过77个token的提示,涉及token_counter的实现、文本提示加权的底层逻辑,以及通过手动拼接和Compel库来扩展提示的两种方法。重点介绍了如何在Transformer模型中应用权重以增强生成效果。https://blog.csdn.net/x1131230123/article/details/137347532
text prompt如何超过77个词
news2026/2/12 18:59:05
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1923068.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
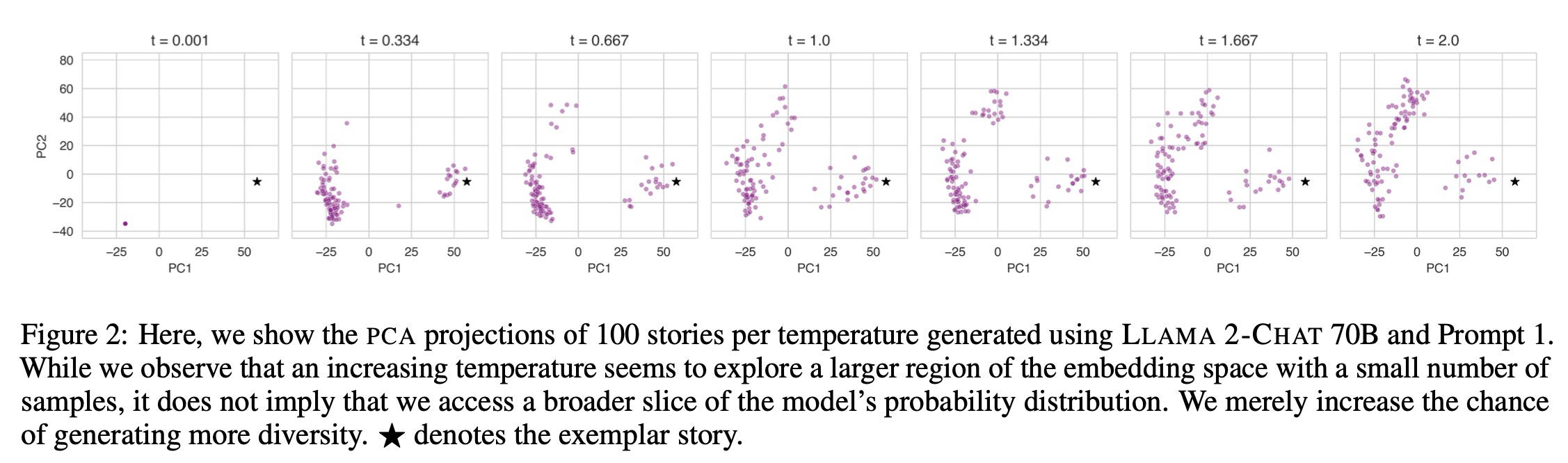
Is Temperature the Creativity Parameter of Large Language Models?阅读笔记
最近有小伙伴来问LLM的参数该如何设计,废话不多说来看看paper吧。首先,常见的可以进行调参的几个值有temperature,top-p和top-k。今天这篇文章是关于temperature的。
原文链接:https://arxiv.org/abs/2405.00492
temperature如果…
基于双向长短期记忆 BiLSTM 实现股票单变量时间序列预测(PyTorch版)
前言 系列专栏:【深度学习:算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域,讨论了各种复杂的深度神经网络思想,如卷积神经网络、循环神经网络、生成对…
SpringBoot新手快速入门系列教程十一:基于Docker Compose部署一个最简单分布式服务项目
我的教程都是亲自测试可行才发布的,如果有任何问题欢迎留言或者来群里我每天都会解答。 如果您还对于Docker或者Docker Compose不甚了解,可以劳烦移步到我之前的教程:
SpringBoot新手快速入门系列教程九:基于docker容器ÿ…
python | setup.py里有什么?
setup.py里有什么? 文章目录 setup.py里有什么?C/C扩展总结gcc/g的编译参数:Windows Visual StudioCmakesetup.py C/C扩展模块 为什么需要分发打包?Distutils一个简单的例子通用的 Python 术语 使用 Setuptools 构建和分发软件包源…
高铁站客运枢纽IPTV电视系统-盐城高铁站西广场IP电视系统应用浅析
高铁站客运枢纽IPTV电视系统-盐城高铁站西广场IP电视系统应用浅析
由北京海特伟业科技有限公司任洪卓于2024年7月9日发布
随着科技的飞速发展,特别是“互联网”战略的深入推进,高铁站客运枢纽的信息化建设成为提升服务质量、增强乘客体验的重要手段。盐…
开发业务(2)——wordpress使用基础教程
外贸领域里面wordpress是比较通用的框架。由于多年的发展,性能和插件非常强大,包括支持各种企业站(很多人已经设计了各种风格,只需要你将对应主题风格安装即可,当然也有付费的)。这导致其内部生态非常强大&…
【C++题解】1231 - 考试成绩的分布情况
问题:1231 - 考试成绩的分布情况
类型:数组基础 题目描述:
期末考试结束,小明的语文老师想知道,这次考试的成绩分布情况,主要计算如下几个数据:平均分、≥ 平均分的总人数、 < 平均分的总人…
linux进程周边知识——内核对硬件的管理——计算机世界的管理
前言:本节主要讲解内核也就是操作系统对于硬件的管理, 本节内容同样为进程的周边知识。 主要是关于软件方面, 和我的上一篇——冯诺依曼体系结构可以说是兄弟文章, 这篇文章主要是关于硬件方面。 两篇文章都是为学习进程做准备。但…
论文翻译 | LEAST-TO-MOST: 从最少到最多的提示使大型语言模型中的复杂推理成为可能
摘要 思维链提示(Chain-of-thought prompting)在多种自然语言推理任务上展现了卓越的性能。然而,在需要解决的问题比提示中展示的示例更难的任务上,它的表现往往不佳。为了克服从简单到困难的泛化挑战,我们提出了一种新…
Spring系统学习 - Spring事务的概念
提到事务,这个我们应该比较熟悉了,在数据库学习的过程中,我们或多或少接触过了事务,当然你可能没有用到,也可能用到了,这篇博客我们将围绕Spring的相关事务的概念进行,了解Spring中的事务和事务…
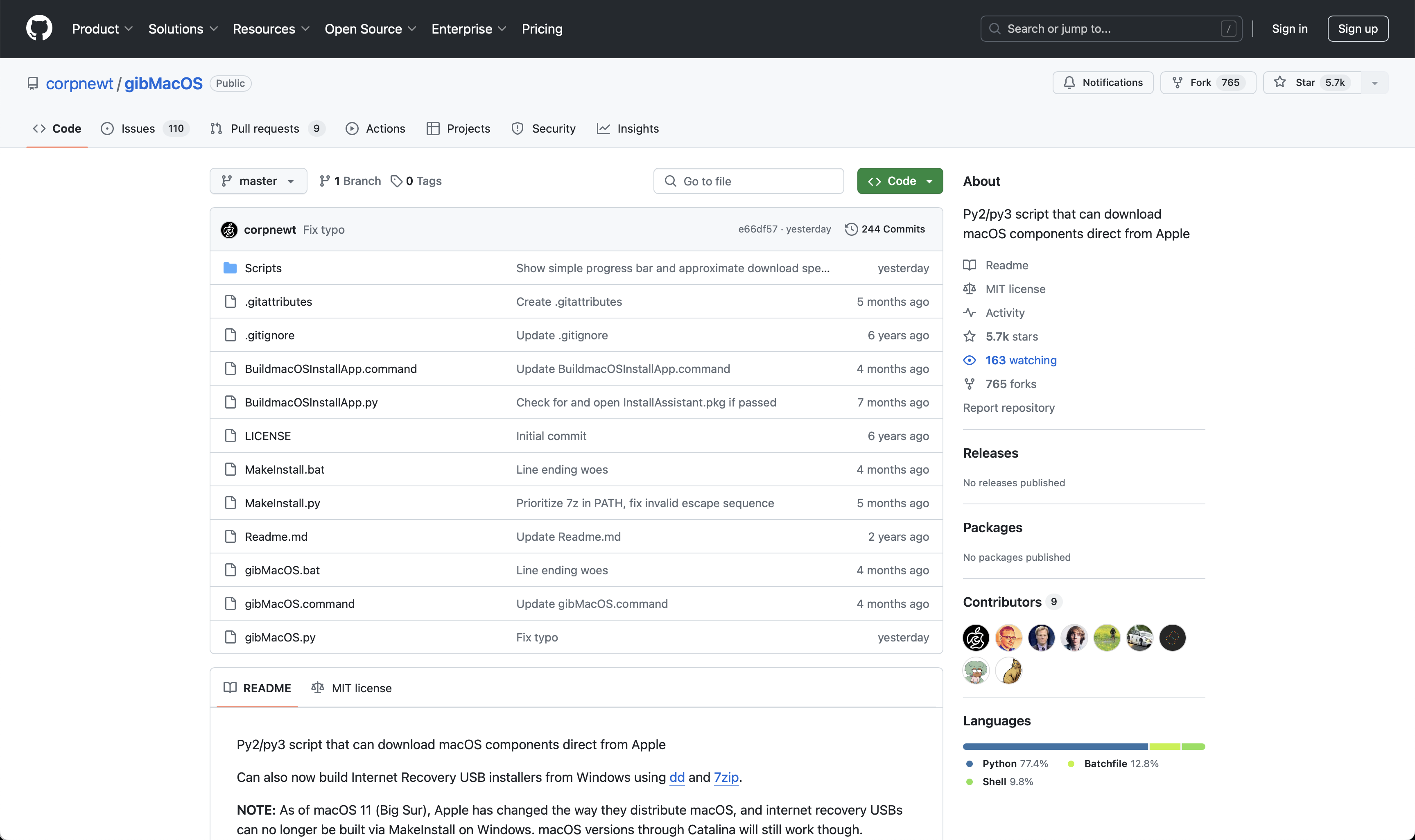
【开源 Mac 工具推荐之 1】gibMacOS:方便快捷的 macOS 完整包下载 Shell 工具
简介
gibMacOS 是由 GitHub 开发者 corpnewt 编写的一款 Shell 工具。它采用 Python 编程语言,可以让用户打开后在纯文本页面中轻松选择并下载来源于 Apple 官方的 macOS 完整安装包。
Repo 地址:https://github.com/corpnewt/gibMacOS (其…
《机器学习中的数学》:探索算法背后的数学奥秘
在当今这个数据驱动的时代,机器学习已经成为科技发展的关键力量。然而,很多人可能不知道,机器学习的高效运作离不开背后的数学基础。今天,我要向大家推荐一本关于机器学习数学基础的书籍——《机器学习中的数学》。这本书不仅详细…
【Python】下载与安装
目录 一、 下载安装Python
1. 配置环境变量
2. 检查是否配置成功 一、 下载安装Python
在我上传的资源可以免费下载!!!
https://download.csdn.net/download/m0_67830223/89536665?spm1001.2014.3001.5501https://download.csdn.net/dow…
cpp随笔——如何实现一个简单的进程守护模块
前言
在前面我们已经实现过调度模块和进程的心跳模块了,而今天我们要讲的是作为服务端后台服务程序运行三个通用模块的最后一项:进程的守护模块,在开始讲解进程的守护模块之前我们首先来看究竟什么是进程的守护模块:
守护模块(有…
torch之从.datasets.CIFAR10解压出训练与测试图片 (附带网盘链接)
前言 从官网上下载的是长这个样子的 想看图片,咋办咧,看下面代码
import torch
import torchvision
import numpy as np
import os
import cv2
batch_size 50transform_predict torchvision.transforms.Compose([torchvision.transforms.ToTensor(),…
Microsoft Graph 是什么?怎么用?
Microsoft Graph 是一个统一的 API 端点,用于访问 Microsoft 云服务中的数据和功能,包括但不限于 Microsoft 365、Dynamics 365、Windows 10、Azure Active Directory (Azure AD) 和其他 Microsoft 服务。通过 Microsoft Graph,开发者和企业可…
钡铼高性能Modbus转EtherCAT网关BL123
随着工业4.0和物联网(IoT)概念的兴起,传统工厂正经历着一场深刻的变革,新型的网络架构,如EtherCAT,因其高速度、高精度及开放性,正在逐渐取代传统的现场总线技术。然而,这并不意味着现有基于旧协议…
【高中数学/指数、对数】已知a=e^0.03-1,b=3/103,c=ln1.03,则a、b、c的大小关系为?
【问题】
已知ae^0.03-1,b3/103,cln1.03,则a、b、c的大小关系为?
【解答】
这个问题比较令人挠头,其背后考察的其实是对ye^x-1,yx/1x,yln(1x)的图线的高度、位置、斜率的掌握程度。
首先我们可以将三个数变成函数式:
ae^0.03-1,b0.03/10…
医日健集团技术力量体现测试的背后
医日健集团覆盖式更新 科技日新月异的时代,医日健集团始终走在行业的前列。近日,医日健集团外勤技术人员全面对市场点位投放的数智药房进行了新系统升级和机器测试,这是医日健对于科技创新的最新尝试。 以客户体验为核心优化新体验 医日健集团…