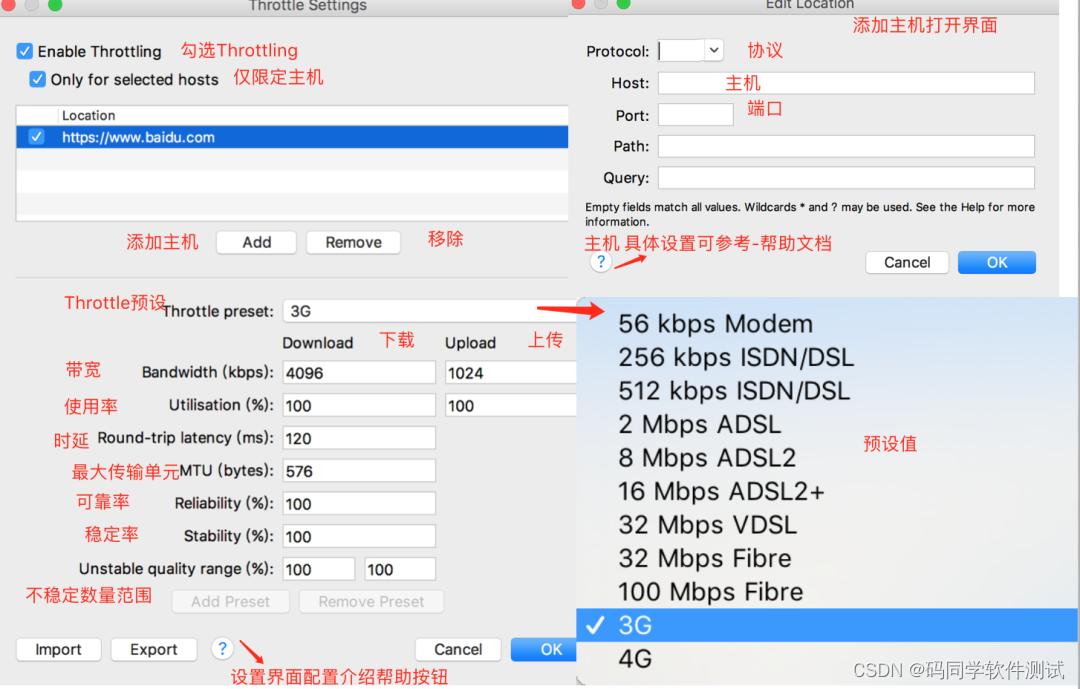
给定二叉树的根节点 root，找出存在于 不同 节点 A 和 B 之间的最大值 V，其中 V = |A.val - B.val|，且 A 是 B 的祖先。

（如果 A 的任何子节点之一为 B，或者 A 的任何子节点是 B 的祖先，那么我们认为 A 是 B 的祖先）

示例 1：

输入：root = [8,3,10,1,6,null,14,null,null,4,7,13]

输出：7

解释：

我们有大量的节点与其祖先的差值，其中一些如下：

|8 - 3| = 5

|3 - 7| = 4

|8 - 1| = 7

|10 - 13| = 3

在所有可能的差值中，最大值 7 由 |8 - 1| = 7 得出。

示例 2：

输入：root = [1,null,2,null,0,3]

输出：3

提示：

• 树中的节点数在 2 到 5000 之间。

• 0 <= Node.val <= 105

https://leetcode.cn/problems/maximum-difference-between-node-and-ancestor/description/?show=1

思路：

对于当前节点来说，只需要计算当前节点的值与其祖先节点中的最大值与最小值的差即可，选取其中大的即为所求

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result = 0; 
    int maxAncestorDiff(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }
        dfs(root, root->val, root->val);
        return result;
    }

    void dfs(TreeNode* root, int up, int low) {
        if(root == nullptr) {
            return;
        }
        // 当前节点的值与其祖先节点中的最大值与最小值的差比较，选取差最大的
        result = max(max(result,abs(root->val - up)),abs(root->val - low));
        // 更新祖先节点中的最大值
        up = max(root->val, up);
        // 祖先节点中的最小值
        low = min(root->val, low);

        dfs(root->left, up, low);
        dfs(root->right, up, low);

    }   

};