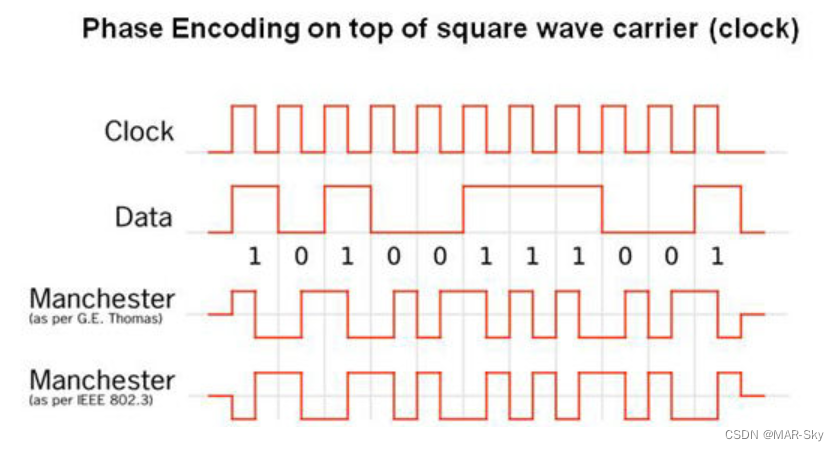
y-hat一般指的就是预测值

---

线性回归模型实例

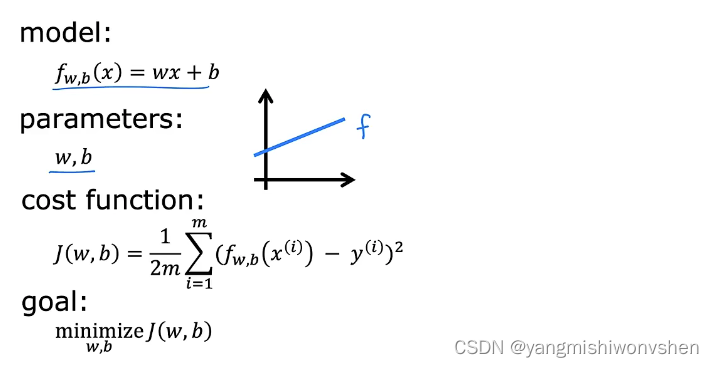
构建模型

我们有一个房子的大小size，得到房屋价格（price），通过这两个常数就可计算一个输入和输出的函数关系。
f _w，b(x⁽ⁱ⁾) = wx⁽ⁱ⁾ +b
i指的是第几个训练数据

评估模型——成本函数

参考链接: link

成本函数和损失函数的区别
机器学习领域我们经常会遇到cost function和loss function(也叫error function)，而这两个function实际是有区别的。loss function通常用于衡量单个样本其预测值和实际值的“差距”，而cost function通常是针对样本集中的所有样本，而且是一个平均值。

通常来说，模型越准确，越接近真实，其cost function的值就越小
在线性回归问题中，通常使用square loss的形式。线性回归常用的square loss形式是均方误差MSE：

选择最优模型——梯度下降法

在训练模型的过程中，我们需要选择一个最符合数据的模型出来，根据上述我们可以知道，成本函数越小，说明训练的模型越能够有较好的预测效果。如下图，回顾整个过程：

一般最小化成本函数是通过梯度下降法（即先随机给出参数的一组值，然后更新参数，使每次更新后的结构都能够让损失函数变小，最终达到最小即可）
如下图，很形象的展示了找到局部最优参数w的过程

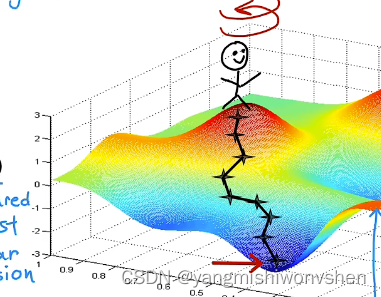
梯度下降如何实现

这里的α是学习率，表示参数更新的步长，α永远是正数，α越大，参数一次调整的幅度越大，很容易无法找到局部最优解，α如果太小了，可以找到局部最优解，但是找局部最优参数的速度就会变得非常慢。

找到局部最优解的情况

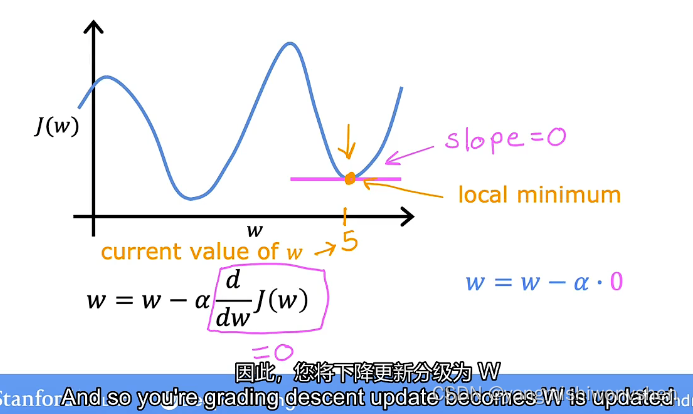
当找到局部最优解的时候，梯度（偏导数）为0，参数w不再更新，将不会再继续进行梯度下降的过程

为什么使用固定的学习率就可以达到局部最优解

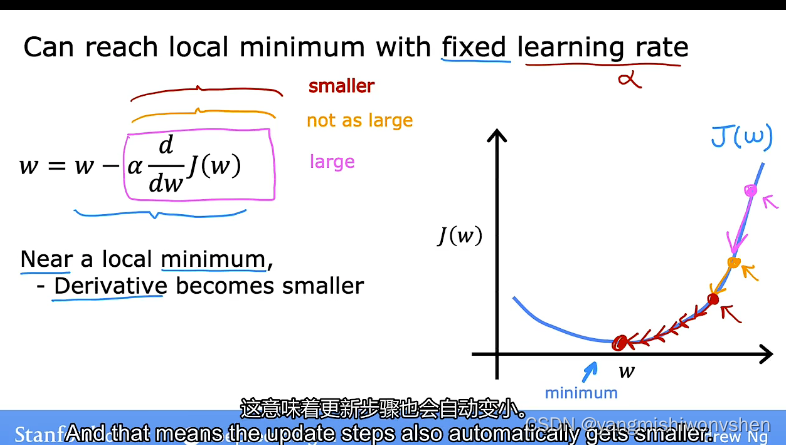
因为随着越来越靠近成本函数局部最小值（收敛）的这个过程中，导数值也会越来越小，参数调整的幅度也会越来越小

线性回归模型的梯度下降公式