🌈🌈😄😄
欢迎来到茶色岛独家岛屿，本期将为大家揭晓LeetCode 300. 最长递增子序列 354. 俄罗斯套娃信封问题，做好准备了么，那么开始吧。
🌲🌲🐴🐴
动态规划
- 首先，动态规划问题的一般形式就是求最值。
- 求解动态规划的核心问题是穷举。
- 动态规划的核心思想就是穷举求最值。
- 明确 base case -> 明确「状态」-> 明确「选择」 -> 定义
dp数组/函数的含义
框架：
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
for 选择 in 所有可能的选择:
# 此时的状态已经因为做了选择而改变
result = 求最值(result, dp(状态1, 状态2, ...))
return result
# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
for 状态2 in 状态2的所有取值：
for ...
for 选择1 in 选择1的所有取值：
for 选择2 in 选择2的所有取值：
排除不合法选择
if()continue;
dp[状态1][状态2][...] = 求最值(选择1，选择2...)
结束条件
return ...知道了这是个动态规划问题，思考如何列出正确的状态转移方程？
1、确定 base case
2、确定「状态」，也就是原问题和子问题中会变化的变量。
3、确定「选择」，也就是导致「状态」产生变化的行为。
4、明确 dp 函数/数组的定义。
300. 最长递增子序列
一、力扣示例
300. 最长递增子序列 - 力扣（LeetCode）
https://leetcode.cn/problems/longest-increasing-subsequence/
二、解决办法
方法一：动态规划
1、确定 base case
int[] dp = new int[nums.length];
// base case：dp 数组全都初始化为 1
Arrays.fill(dp, 1);
2、确定「状态」，也就是原问题和子问题中会变化的变量。dp[i]
3、确定「选择」，也就是导致「状态」产生变化的行为。dp[j]，遍历小于i之前的dp[j]，求最大dp[j]，再加一得dp[i]
4、明确 dp 函数/数组的定义。dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
class Solution {
public int lengthOfLIS(int[] nums) {
// dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
int[] dp = new int[nums.length];
// base case：dp 数组全都初始化为 1
Arrays.fill(dp, 1);
//自底向上
for (int i = 0; i < nums.length; i++)//状态，变量为dp[i]
{
for (int j = 0; j < i; j++) //选择，产生变化的行为是dp[j]
{
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
这个解法不是最优的，可能无法通过所有测试用例
方法二：二分查找，此方法更高效，通过所有测试用例
这个解法的时间复杂度为 O(NlogN)
首先定义了一个数组 top，用来存储当前已经处理好的 LIS 的顶部，即存储每一堆牌的最高牌。对于输入数组的每一个元素，都将其看作一张要处理的扑克牌。
接着，开始进行二分查找，以找到一个合适的牌堆，使得当前这张牌能够放入。在查找过程中，如果当前的牌堆顶的牌比要处理的扑克牌高，那么搜索区间的右端点变为中间位置；如果当前的牌堆顶的牌比要处理的扑克牌低，那么搜索区间的左端点变为中间位置加 1；如果当前的牌堆顶的牌和要处理的扑克牌相等，那么右端点也变为中间位置。
最后，如果没有找到合适的牌堆，就需要新建一堆。否则，将当前这张牌放入找到的牌堆顶。
完成对所有元素的处理后，牌堆数即为最长上升子序列的长度，最后通过返回 piles 的值来表示 LIS 的长度。
总的来说就是不断遍历数组元素通过二分查找找到每个元素位置，然后计算能有几堆（piles 长度）为最长上升子序列的长度。
class Solution {
public int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
// 牌堆数初始化为 0
int piles = 0;
for (int i = 0; i < nums.length; i++) {
// 要处理的扑克牌
int poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
/*********************************/
// 没找到合适的牌堆，新建一堆
if (left == piles) piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
}
354. 俄罗斯套娃信封问题
一、力扣示例
354. 俄罗斯套娃信封问题 - 力扣（LeetCode）https://leetcode.cn/problems/russian-doll-envelopes/
二、解决办法
这道题目其实是最长递增子序列的一个变种，相当于在二维平面中找一个最长递增的子序列，其长度就是最多能嵌套的信封个数。
二分查找
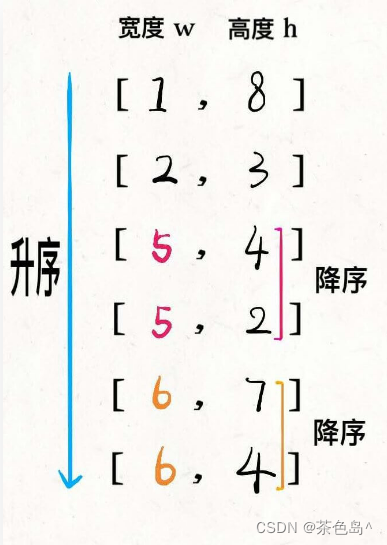
解法：先对宽度 w 进行升序排序，如果遇到 w 相同的情况，则按照高度 h 降序排序；之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。
class Solution {
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// 按宽度升序排列，如果宽度一样，则按高度降序排列
Arrays.sort(envelopes, new Comparator<int[]>()
{
public int compare(int[] a, int[] b) {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
}
});
// 对高度数组寻找 LIS
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
// 牌堆数初始化为 0
int piles = 0;
for (int i = 0; i < nums.length; i++) {
// 要处理的扑克牌
int poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
// 没找到合适的牌堆，新建一堆
if (left == piles) piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
}
