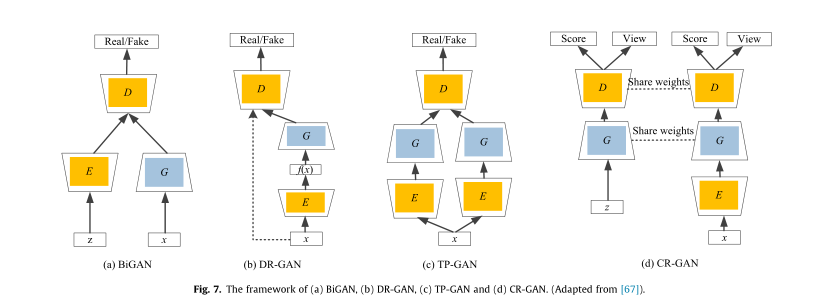
三维图形的绘制
- 生成绘图所需的横纵坐标
- 三维网格图的绘制
- 基本语法
- 实战案例
- 两种变形函数
- 三维曲面图的绘制
- 两种变形函数
- 绘图效果的优化
- 其他补充内容
生成绘图所需的横纵坐标
[X,Y]=meshgrid(xgv,ygv)
% 函数解释:X和Y是用于接收返回值的变量,是两个大小相等的矩阵
% xgv和ygv是分别用于表示x和y取值范围的行向量,如果省略一个则默认x和y取值范围相同。
% 函数原理:X由xgv复制length(ygv)行得到,Y首先ygv进行转置,再将ygv'复制length(xgv)次得到。
三维网格图的绘制
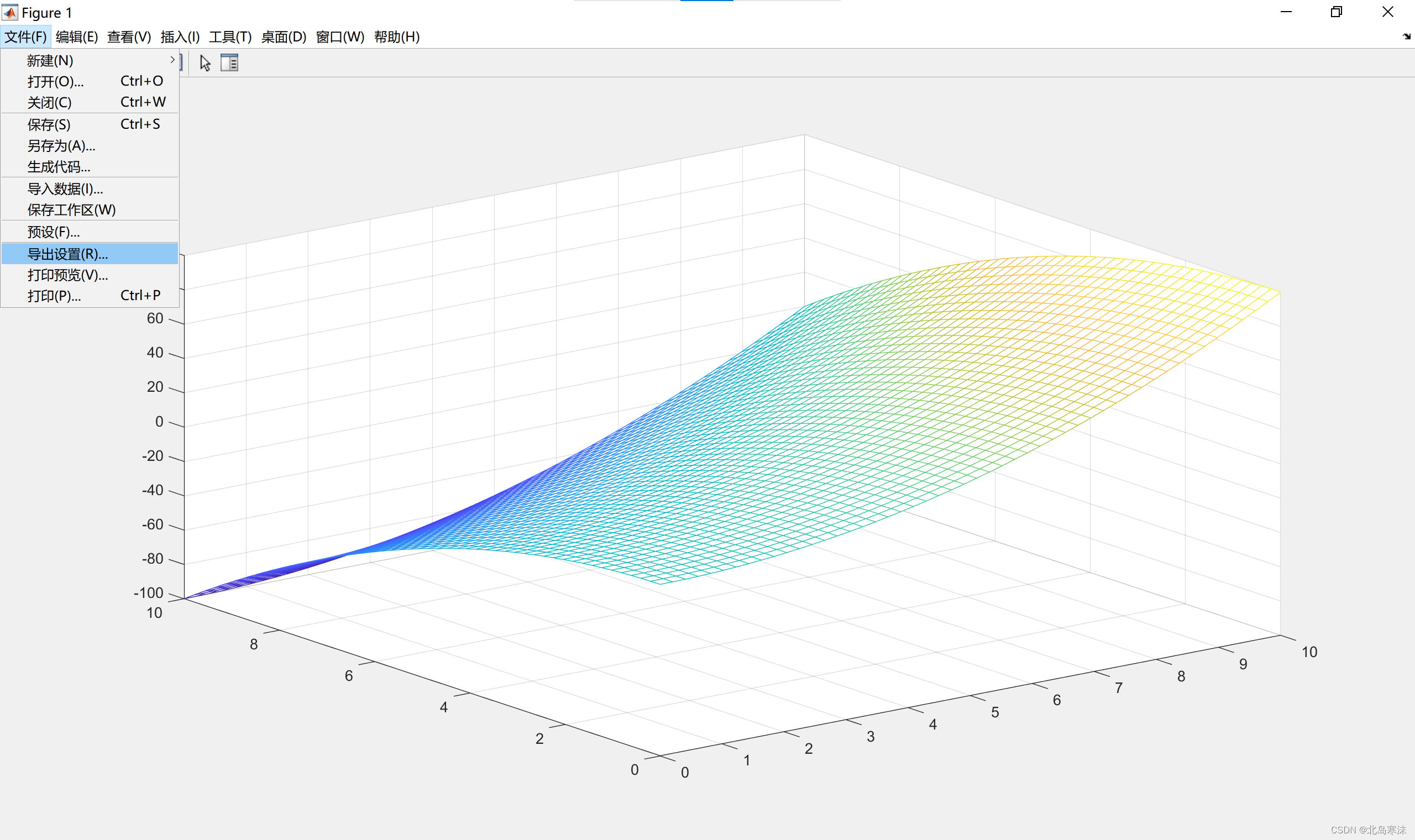
网格图绘制效果:由多个网格拼接构成的图形称为网格图。网格图可以用于二元函数图像的绘制。
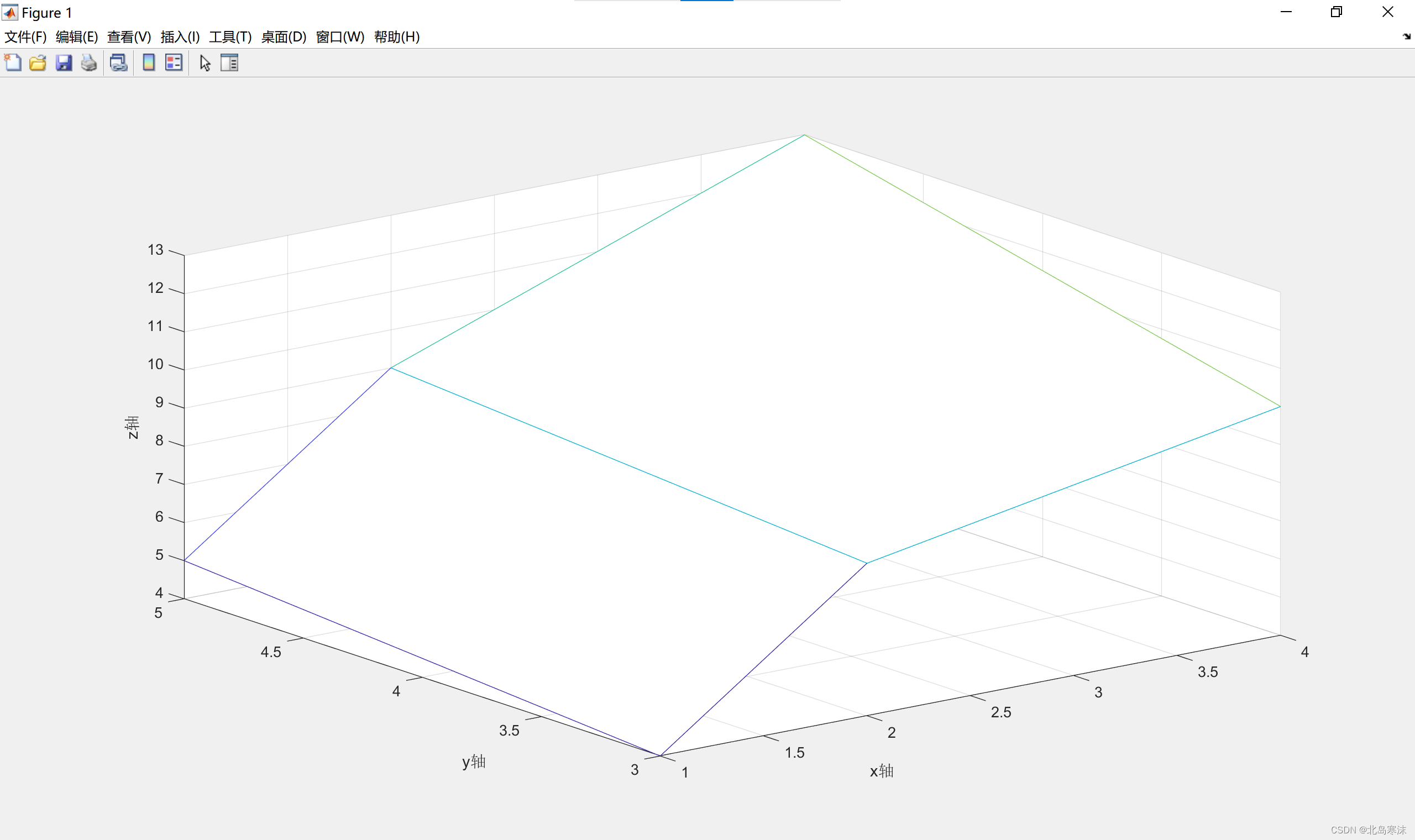
基本语法
1.mesh(X,Y,Z):最基础的使用语法。
% 其中X是n维行向量,Y是m维行向量,Z是m×n的矩阵。
% 函数解释:构造的三维点共有m×n个,每一个三维点的坐标为(X(j),Y(i),Z(i,j)))
% 理解方式:相当于对X和Y向量中相邻的两个元素(对应四个点)绘制一个三维平面,然后再向后挪一个,对下一对相邻元素绘制一个三位平面,最后把绘制的所有三维平面拼接在一起。
% 函数的绘图结果中线条的颜色反映了点的高度。
2.mesh(Z):最基础使用语法的简化形式。
% 其中Z是一个m×n的矩阵。
% 函数解释:省略了X和Y向量,默认X是从1到Z矩阵列数的等差数列向量,Y是从1到Z矩阵行数的等差数列向量。
3.mesh(X,Y,Z):mesh函数最常用的语法形式。
% 其中X和Y和Z都是m×n的矩阵。
% 第一种形式中X和Y分别是m维和n维行向量,系统会自动将X和Y分别重复扩展为m×n的矩阵,变为第三种形式。
% 函数解释:定义了X、Y和Z三个矩阵后相当于得到了一个由三维点坐标构成的矩阵,对坐标点矩阵中所有行列相邻的四个元素绘制一个平面,拼接在一起就构成了最终的网格图。
实战案例
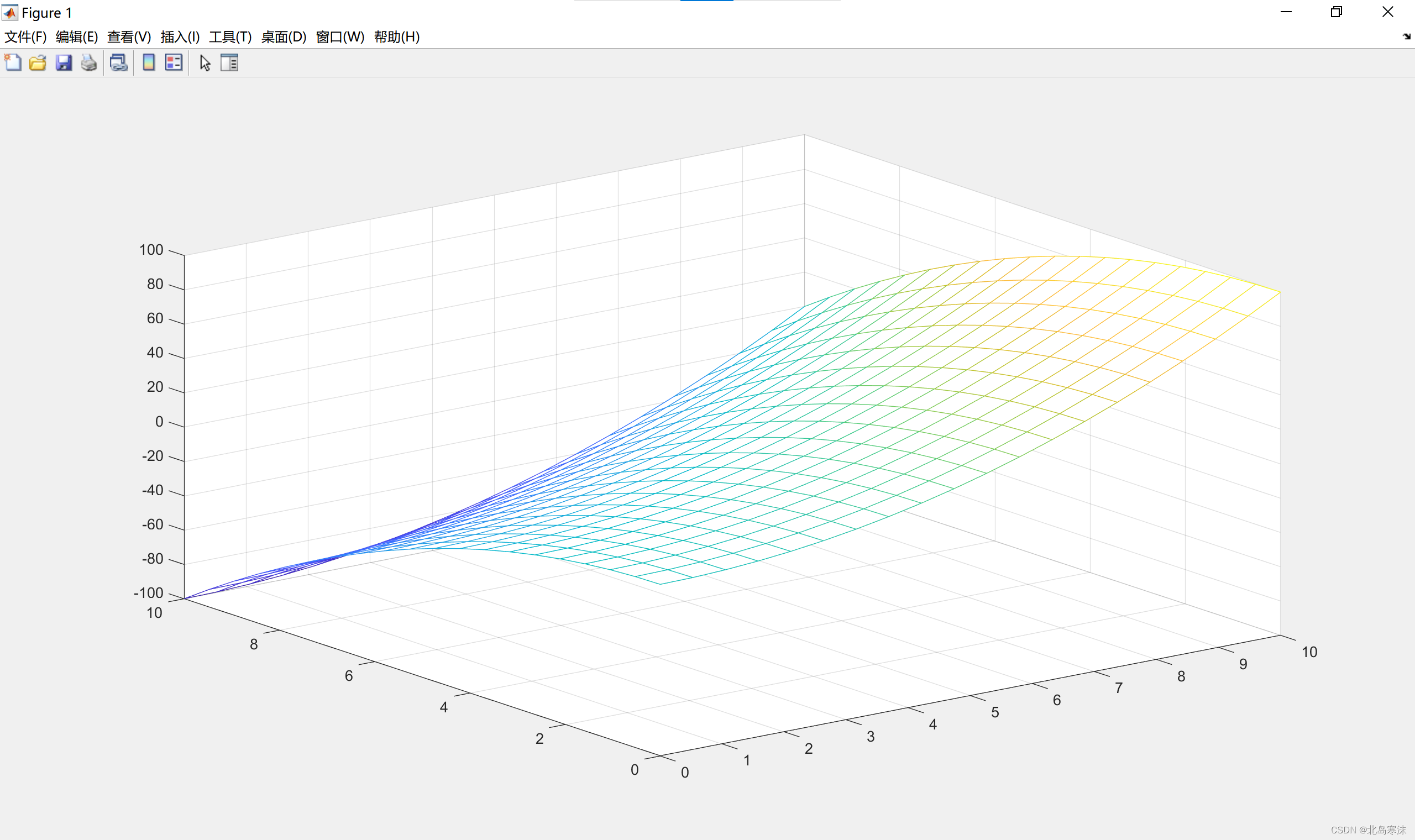
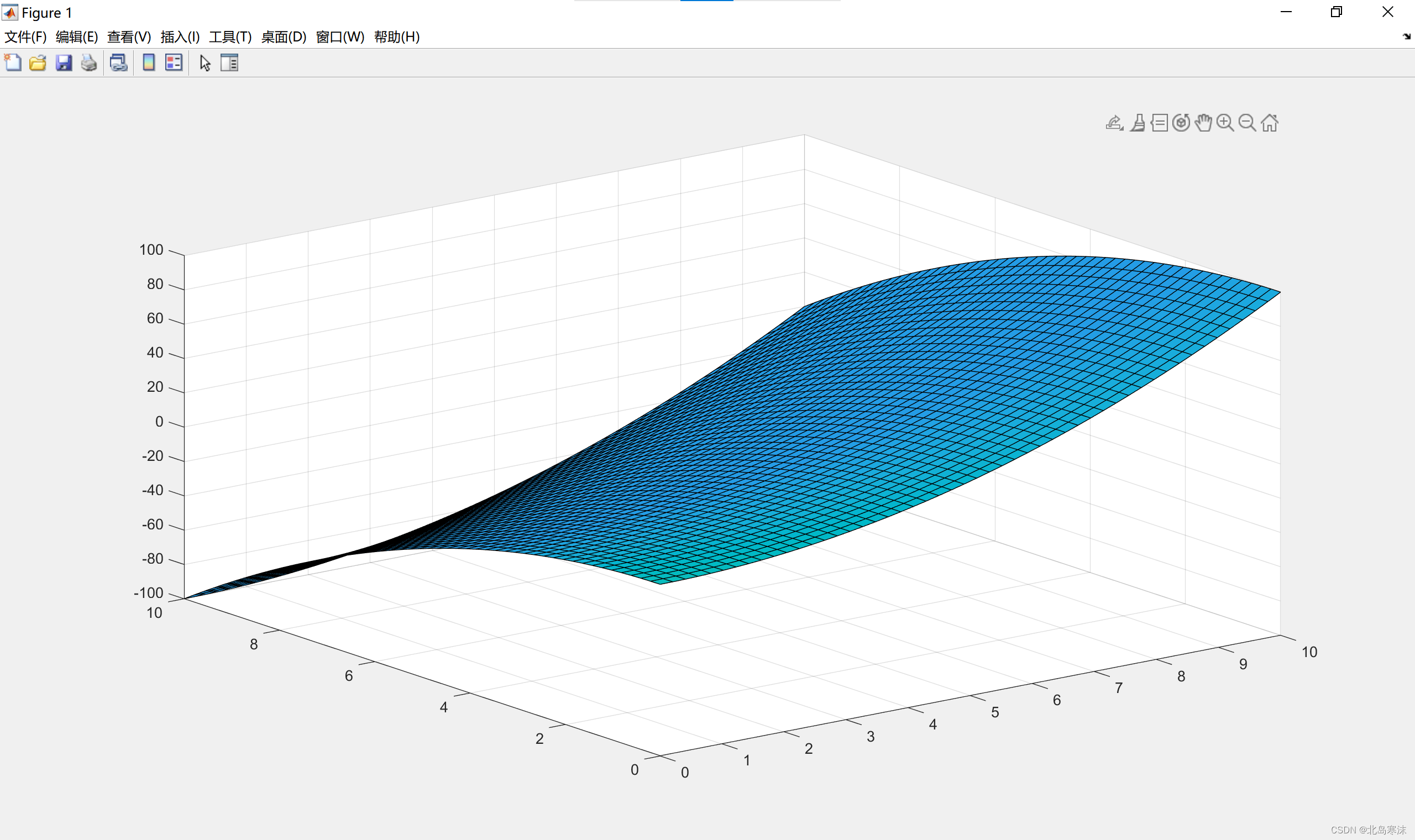
题目要求:绘制z=x²-y平方的函数图像,其中x和y的取值范围都是[0,10]。
绘制Matlab代码:
X=repmat(linspace(0,10,20),20,1)
Y=repmat(linspace(0,10,20)',1,20);
% 此处X和Y的生成过程可以用meshgrid函数代替:[X,Y]=meshgrid(linspace(0,10,20)
Z=X.*X-Y.*Y;
mesh(X,Y,Z)
绘制效果图:
两种变形函数
- meshc函数:mesh函数的变形,绘制结果带有等高线底线。
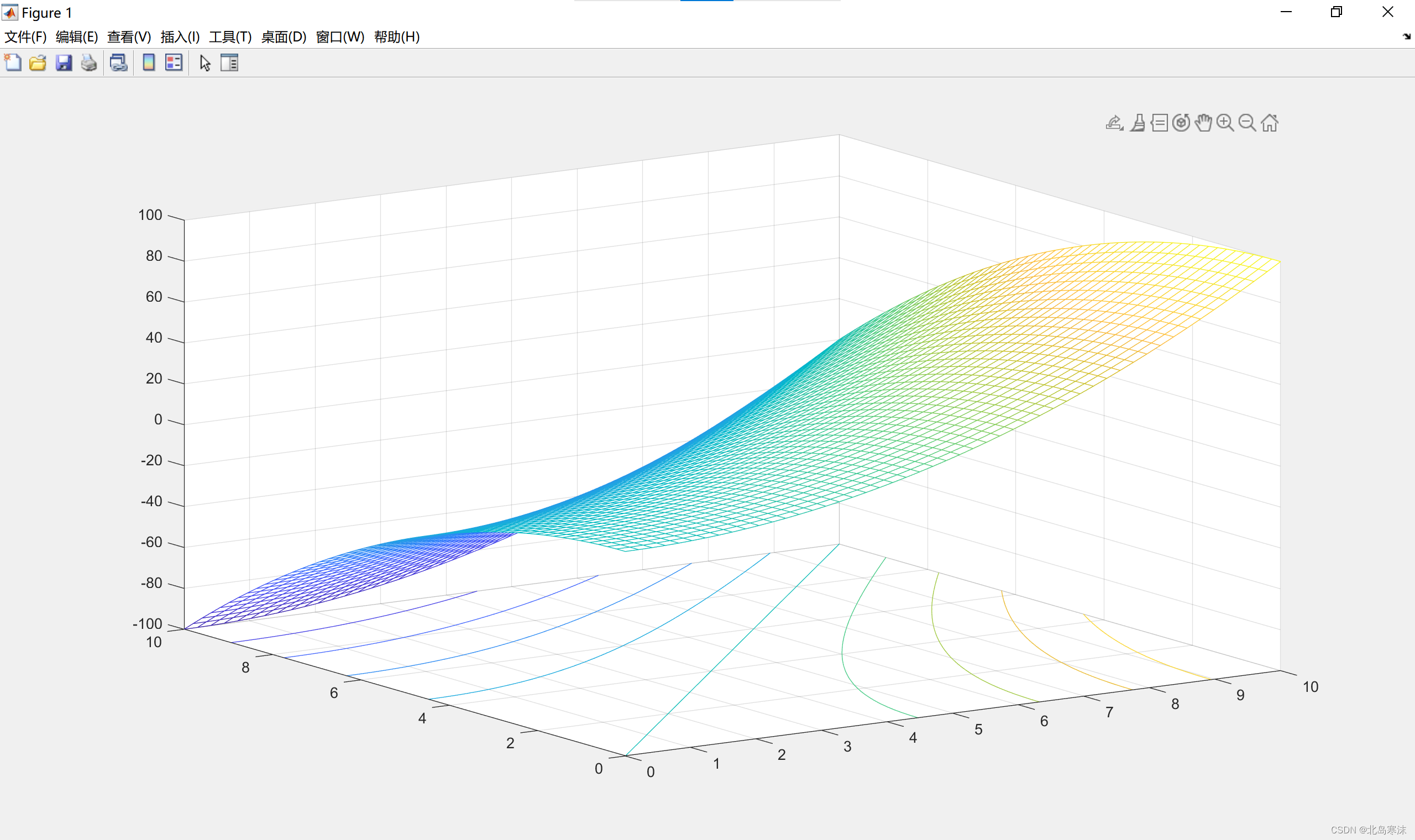
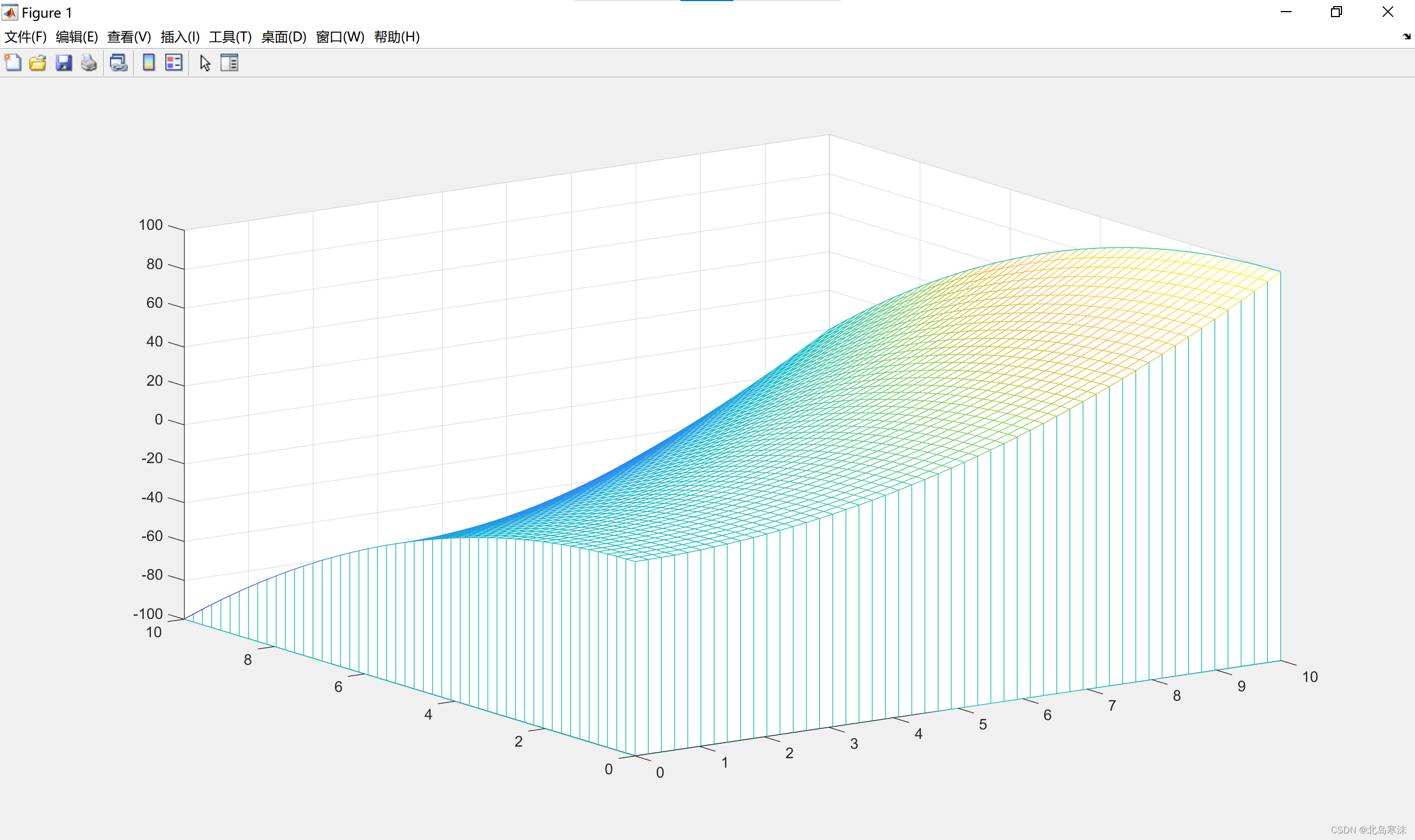
- meshz函数:mesh函数的变形,增加绘制了曲面的底座。(使用较少)
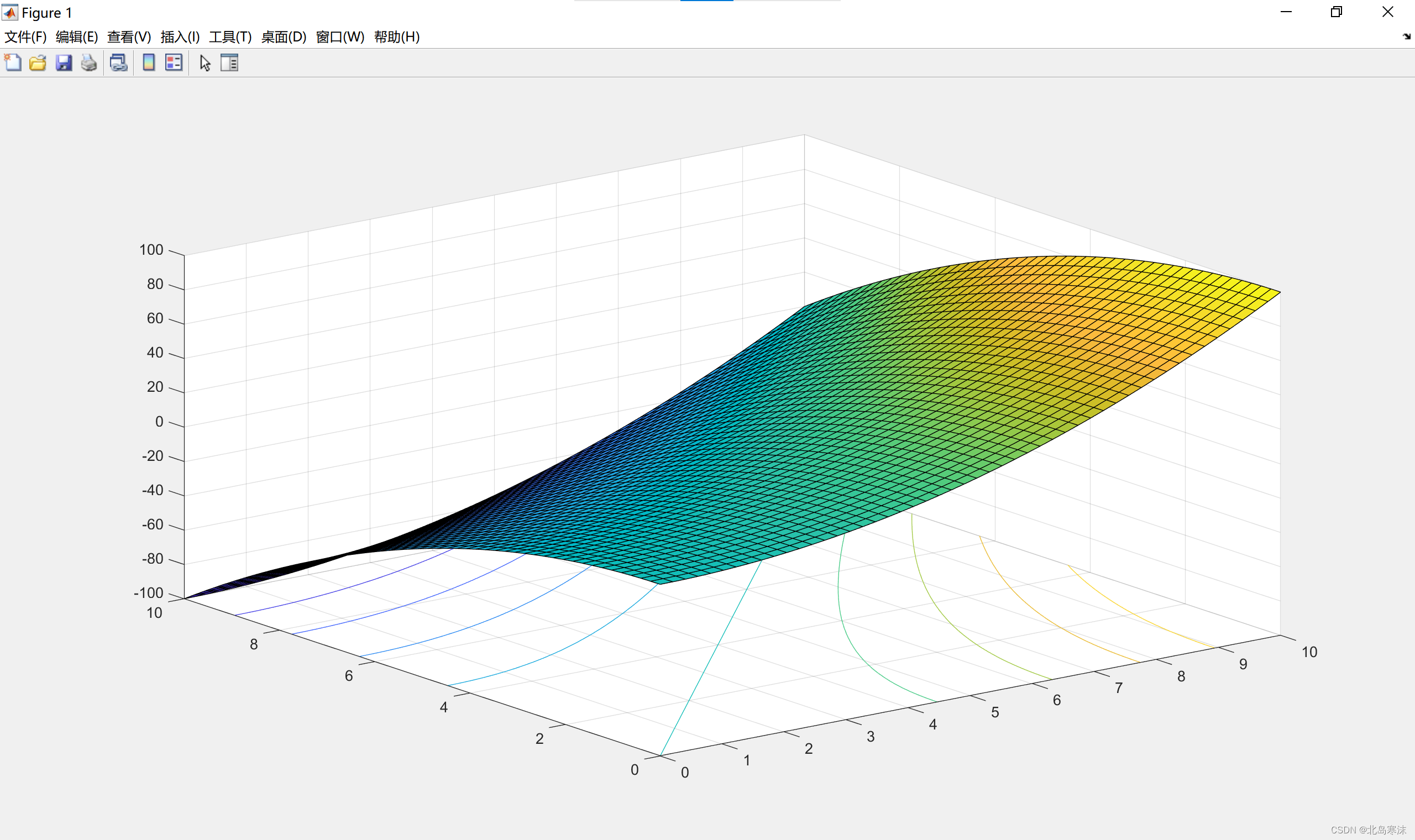
三维曲面图的绘制
曲面图绘制效果:
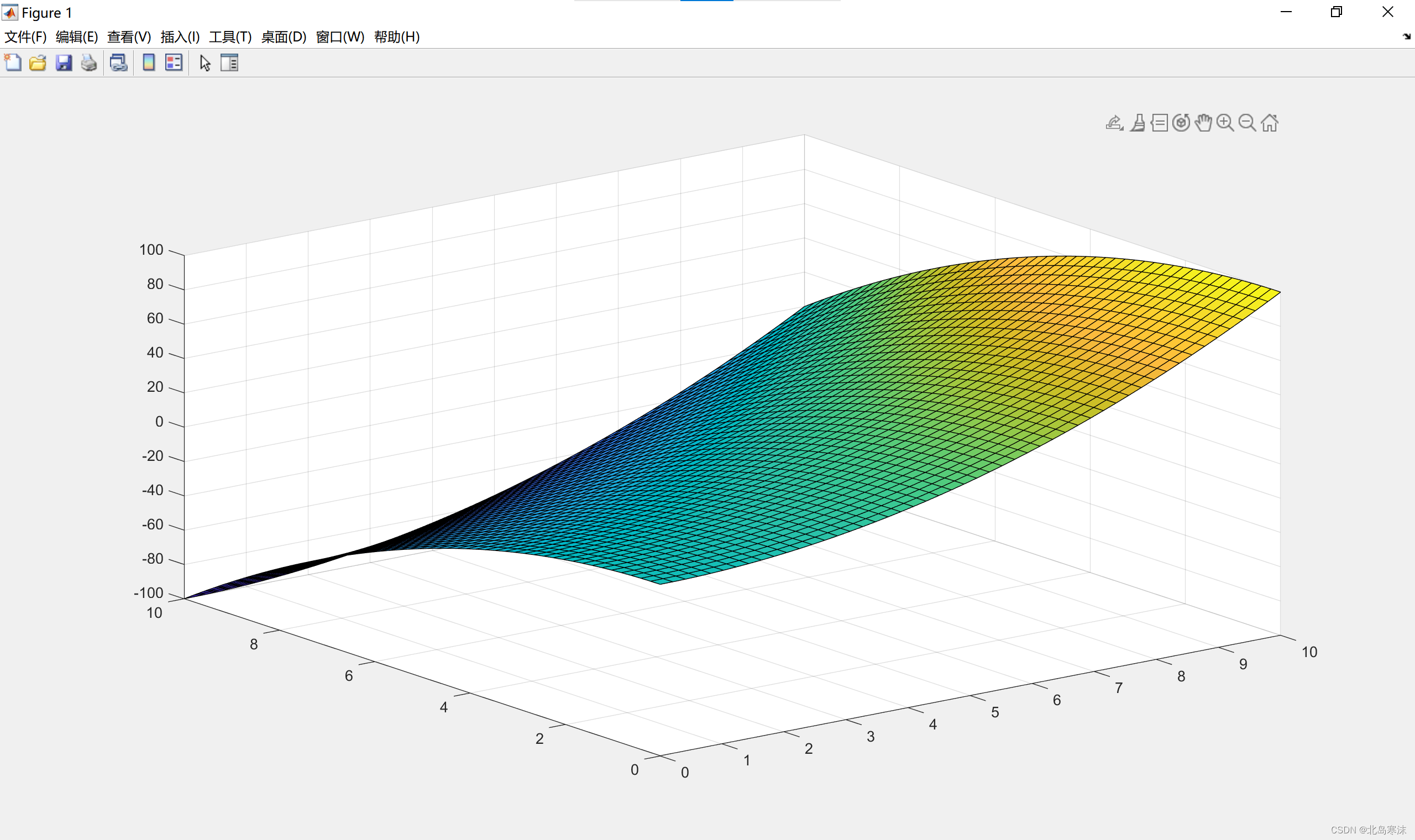
绘制语法:与进行三维网格图绘制的mesh函数语法完全相同。
两种变形函数
- surfc函数:surf函数的变形,绘制结果带有等高线底线。
- surfl函数:surf函数的变形,绘制结果带有灯光效果。
绘图效果的优化
- 透明度设置:
alpha(透明度)
函数解释:用来设置绘图的透明度,用于优化绘图效果。
透明度:一个0-1之间的浮点数(小数)。
- 设置坐标轴标签:
xlabel("X轴");ylabel("Y轴");zlabel("Z轴");
- 旋转不改变坐标轴尺度(根据需要选择):
axis vid3d;
% 对于含有subplot的图,需要对每一个图都使用才能保证相同的坐标轴效果。
- 设置绘图子图(根据需要选择):
subplot(图行数,图列数,图序号)
% 图的序号是在母图中逐行标号的。
- 设置图像标题:
title(标题字符串)
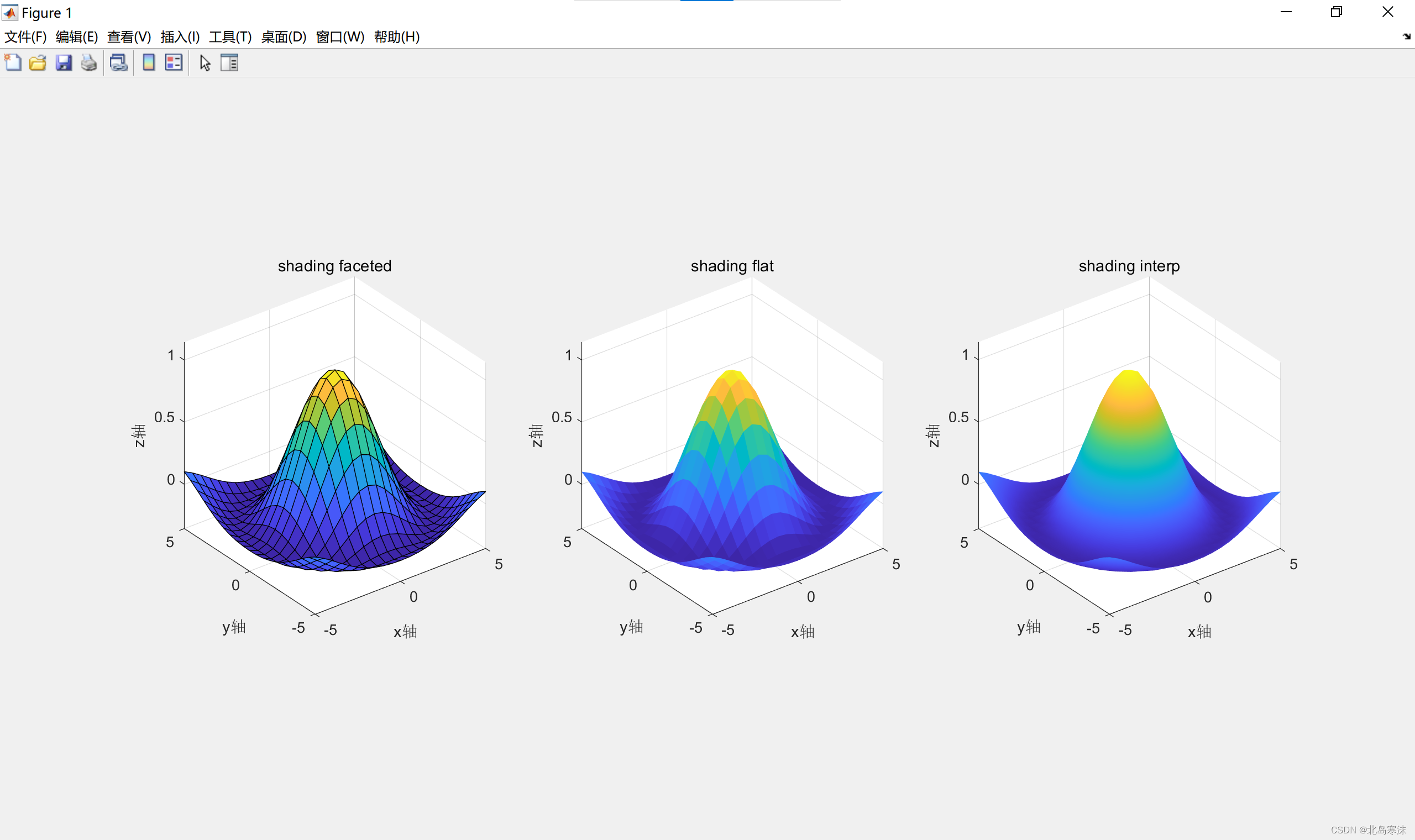
- 设置色彩模式
% 通过shading可以设置绘图的色彩模式
shading faceted %默认采用的模式
shading flat %去掉了绘制结果的网格线
shading interp %在flat的基础上实现了色彩的平滑过渡
其他补充内容
- 绘图值出现非数NaN:常常由0/0导致,此时可以在被除数0后加一个Matlab常数eps来避免出现非数。
- 绘图结果的高清导出:注意需要设置尽可能高的分辨率。