- 1. 线性回归
- 1.1线性回归理论
- 1.2线性回归实战
- 2.分类模型评估(Mnist实战SGD_Classifier)
- 2.1 K折交叉验证K-fold cross validation
- 2.2 混淆矩阵Confusion Matrix
- 2.3 准确率accuracy、精度precision、召回率recall、F1
- 2.4 置信度confidence
- 2.5 ROC曲线
- 3.训练调参基本功(LinearRegression)
- 3.1 线性回归模型实现
- 3.2不同GD策略对比
- 3.3多项式曲线回归
- 3.4过拟合和欠拟合
- 3.5正则化作用
- 3.6EarlyStop提前停止
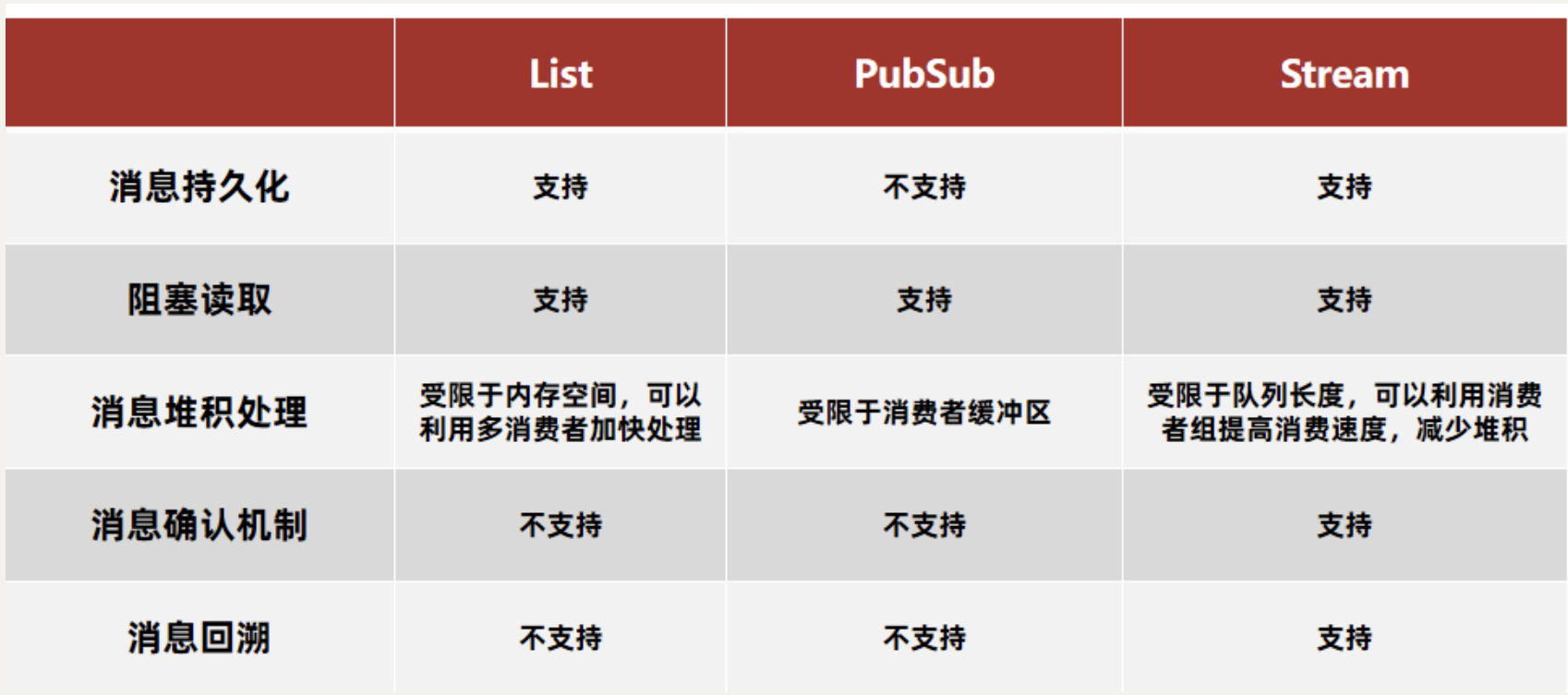
机器学习模型的参数,不是直接数学求解,而是利用数据,进行迭代epoch,梯度下降优化求解。
1. 线性回归
1.1线性回归理论
-
目标:更好的拟合连续函数(分割连续样本空间的平面h(·))

-
ε ( i ) \varepsilon^{(i)} ε(i)是 真实值 y ( i ) y^{(i)} y(i) 与 预测值 h θ ( x ) = θ T x ( i ) h_\theta (x)=\theta^Tx^{(i)} hθ(x)=θTx(i)之间的误差

-
求解参数 θ \theta θ :误差项 ε \varepsilon ε服从高斯分布,利用最大似然估计,转换为最小二乘法
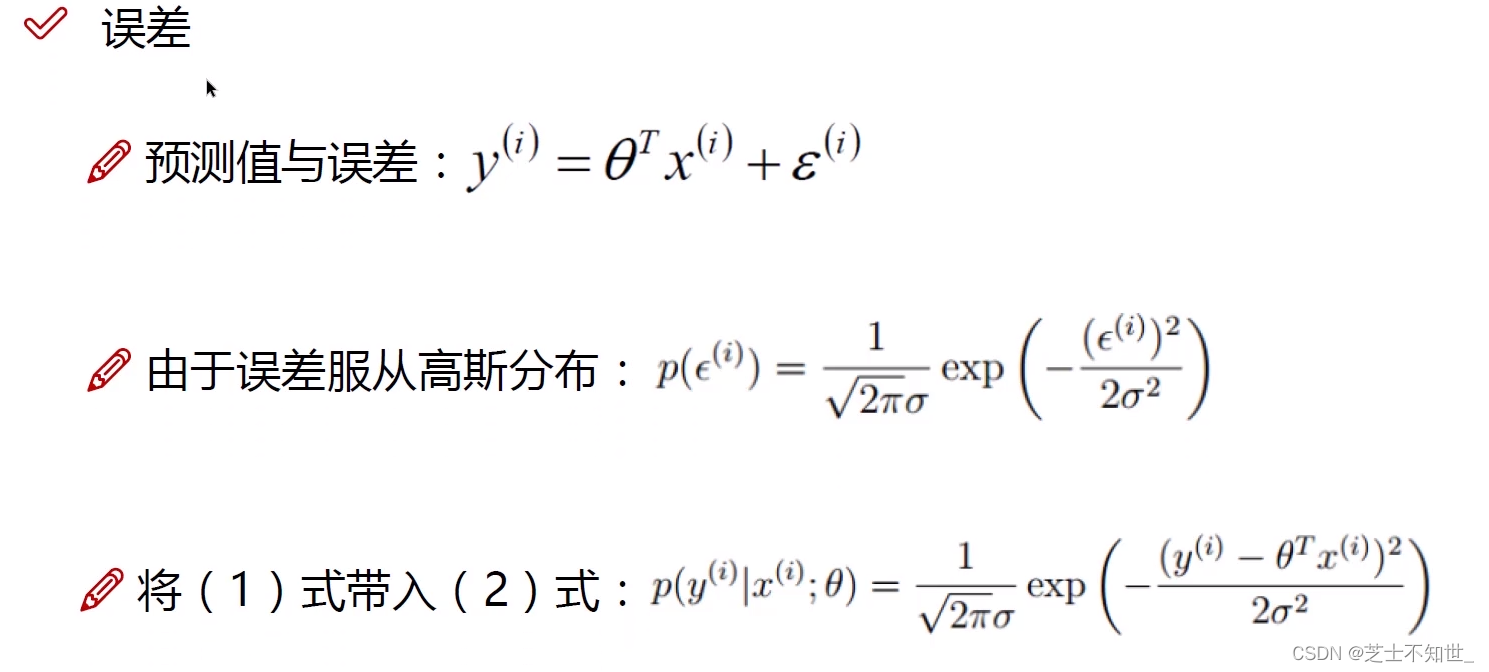


-
从最小二乘法得到目标函数 J ( θ ) J(\theta) J(θ),为求其最值,利用梯度下降算法,沿偏导数(梯度)反方向,迭代更新计算,求解参数 θ \theta θ 。
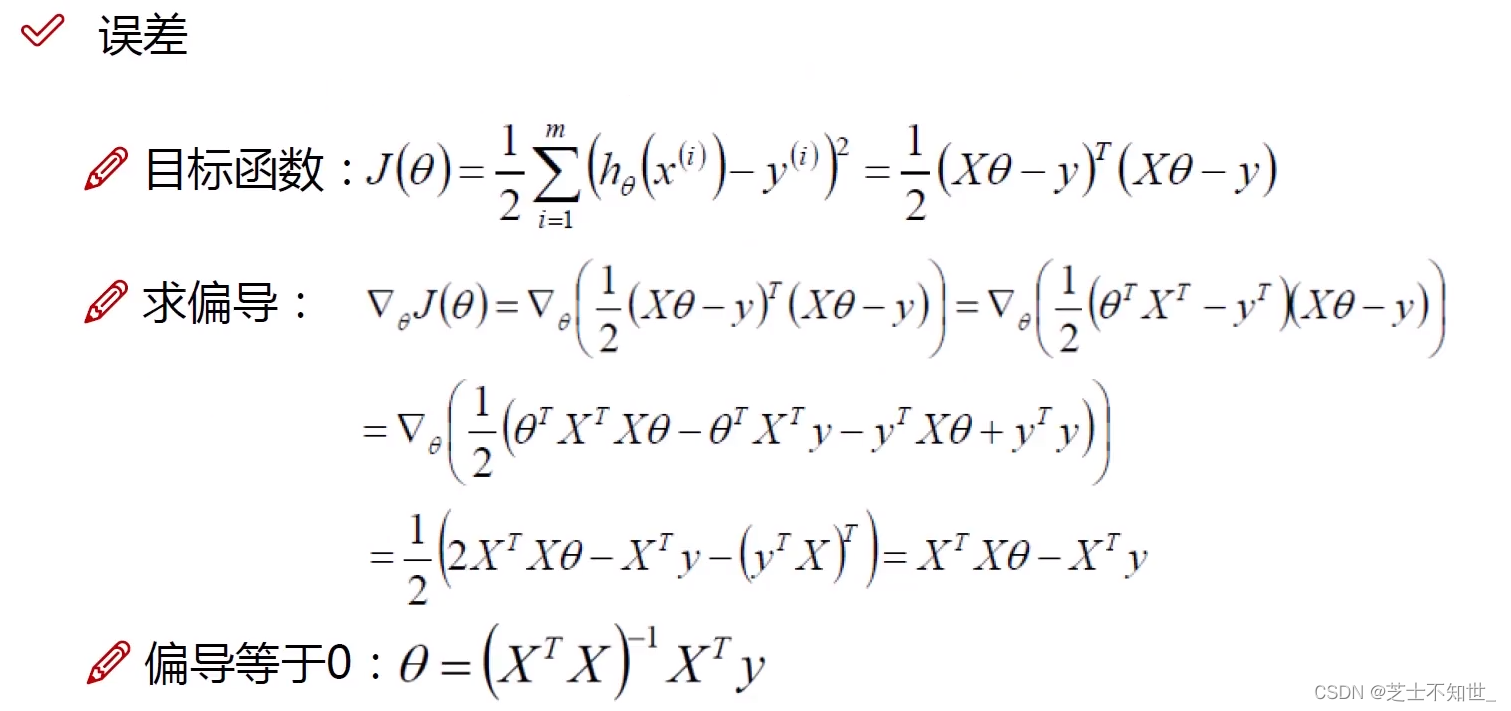
-
梯度下降算法:BatchGD批量梯度下降、SGD随机梯度下降、Mini-BatchGD小批量梯度下降(实用)
batch一般设为 2 5 2^5 25=64、 2 6 2^6 26=128、 2 7 2^7 27=256,越大越好


GD的矩阵运算:

-
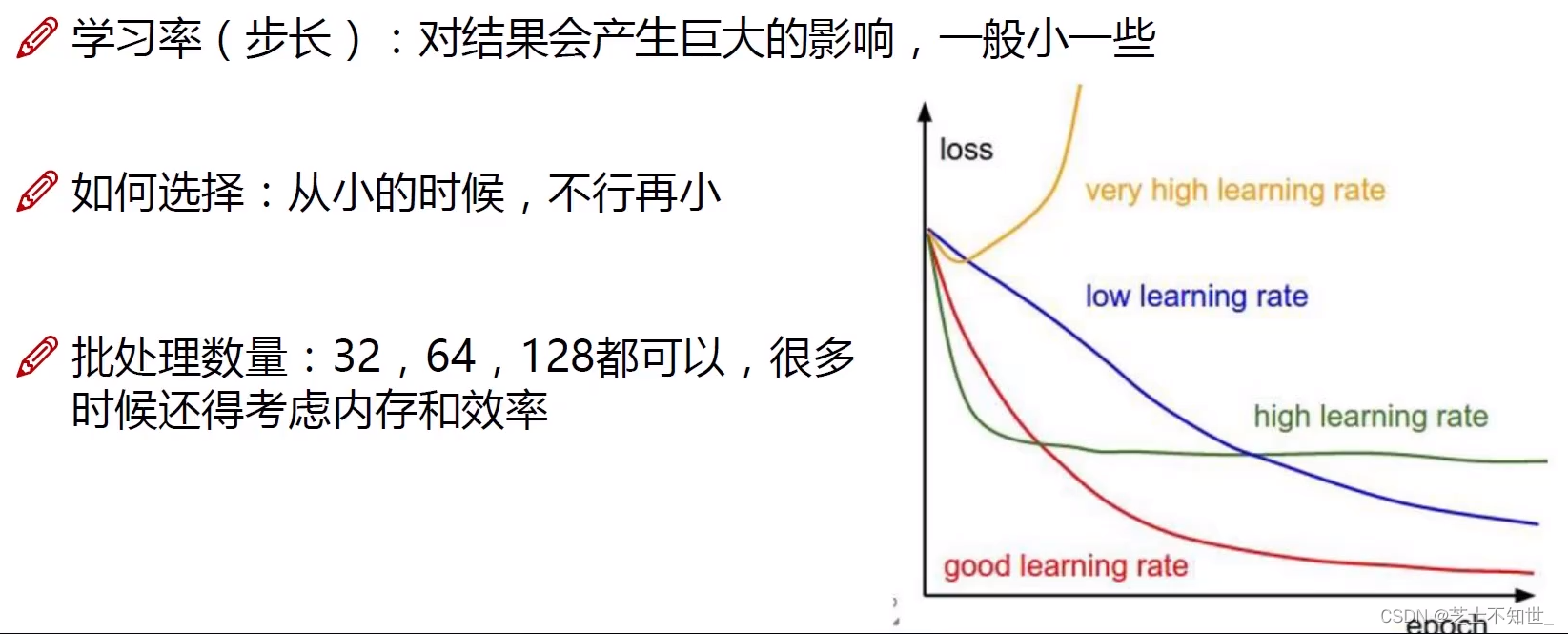
学习率lr:开始设1e-3,逐渐调小到1e-5
1.2线性回归实战
数据预处理中normalize标准化作用:对输入全部数据 X − μ σ \frac{ X-\mu}{\sigma } σX−μ,使得不同值域的输入 x i x_i xi、 x j x_j xj分布在同一取值范围。如 x i ∈ [ 0.1 , 0.5 ] x_i\in[0.1, 0.5] xi∈[0.1,0.5], x j ∈ [ 10 , 50 ] x_j\in[10, 50] xj∈[10,50],normalize使其同一值域。
prepare__for_train.py
"""Prepares the dataset for training"""
import numpy as np
from .normalize import normalize
from .generate_sinusoids import generate_sinusoids
from .generate_polynomials import generate_polynomials
def prepare_for_training(data, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):
# 计算样本总数
num_examples = data.shape[0]
data_processed = np.copy(data)
# 预处理
features_mean = 0
features_deviation = 0
data_normalized = data_processed
if normalize_data:
(
data_normalized,
features_mean,
features_deviation
) = normalize(data_processed)
data_processed = data_normalized
# 特征变换sinusoidal
if sinusoid_degree > 0:
sinusoids = generate_sinusoids(data_normalized, sinusoid_degree)
data_processed = np.concatenate((data_processed, sinusoids), axis=1)
# 特征变换polynomial
if polynomial_degree > 0:
polynomials = generate_polynomials(data_normalized, polynomial_degree, normalize_data)
data_processed = np.concatenate((data_processed, polynomials), axis=1)
# 加一列1
data_processed = np.hstack((np.ones((num_examples, 1)), data_processed))
return data_processed, features_mean, features_deviation
linearRegressionClass.py
class LinearRegression_:
def __init__(self, data, labels, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):
"""
1.对数据进行预处理操作
2.先得到所有的特征个数
3.初始化参数矩阵
"""
(data_processed,
features_mean,
features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data=True)
self.data = data_processed
self.labels = labels
self.features_mean = features_mean
self.features_deviation = features_deviation
self.polynomial_degree = polynomial_degree
self.sinusoid_degree = sinusoid_degree
self.normalize_data = normalize_data
num_features = self.data.shape[1]
self.theta = np.zeros((num_features, 1))
def train(self, alpha=0.01, num_iterations=500):
"""
训练模块,执行梯度下降
"""
cost_history = self.gradient_descent(alpha, num_iterations)
return self.theta, cost_history
def gradient_descent(self, alpha, num_iterations):
"""
实际迭代模块,会迭代num_iterations次
"""
cost_history = []
for _ in range(num_iterations):
self.gradient_step(alpha)
cost_history.append(self.cost_function(self.data, self.labels))
return cost_history
def gradient_step(self, alpha):
"""
梯度下降参数更新计算方法,注意是矩阵运算
"""
num_examples = self.data.shape[0]
prediction = LinearRegression_.hypothesis(self.data, self.theta)
delta = prediction - self.labels
theta = self.theta
theta = theta - alpha * (1 / num_examples) * (np.dot(delta.T, self.data)).T
self.theta = theta
def cost_function(self, data, labels):
"""
损失计算方法
"""
num_examples = data.shape[0]
delta = LinearRegression_.hypothesis(self.data, self.theta) - labels
cost = (1 / 2) * np.dot(delta.T, delta) / num_examples
return cost[0][0]
@staticmethod
def hypothesis(data, theta):
predictions = np.dot(data, theta)
return predictions
def get_cost(self, data, labels):
data_processed = prepare_for_training(data,
self.polynomial_degree,
self.sinusoid_degree,
self.normalize_data
)[0]
return self.cost_function(data_processed, labels)
def predict(self, data):
"""
用训练的参数模型,与预测得到回归值结果
"""
data_processed = prepare_for_training(data,
self.polynomial_degree,
self.sinusoid_degree,
self.normalize_data
)[0]
predictions = LinearRegression_.hypothesis(data_processed, self.theta)
return predictions
单输入变量线性回归:
y
=
θ
1
x
1
+
b
y=\theta^1x^1+b
y=θ1x1+b
single_variate_LinerRegression.py
import os
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from linearRegressionClass import *
dirname = os.path.dirname(__file__)
data = pd.read_csv(dirname + "/data/world-happiness-report-2017.csv", sep=',')
train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)
# 选定考虑的特征
input_param_name = 'Economy..GDP.per.Capita.'
output_params_name = 'Happiness.Score'
x_train = train_data[[input_param_name]].values
y_train = train_data[[output_params_name]].values
x_test = test_data[[input_param_name]].values
y_test = test_data[[output_params_name]].values
# 用创建的随机样本测试
# 构造样本的函数
# def fun(x, slope, noise=1):
# x = x.flatten()
# y = slope*x + noise * np.random.randn(len(x))
# return y
# # 构造数据
# slope=2
# x_max = 10
# noise = 0.1
# x_train = np.arange(0,x_max,0.2).reshape((-1,1))
# y_train = fun(x_train, slope=slope, noise=noise)
# x_test = np.arange(x_max/2, x_max*3/2, 0.2).reshape((-1,1))
# y_test = fun(x_test, slope=slope, noise=noise)
# #观察训练样本和测试样本
# # plt.scatter(x_train, y_train, label='train data', c='b')
# # plt.scatter(x_test, y_test, label='test data', c='k')
# # plt.legend()
# # plt.title('happiness - GDP')
# # plt.show()
# #测试 - 与唐宇迪的对比
# lr = LinearRegression()
# lr.fit(x_train, y_train)
# print(lr.predict(x_test))
# print(y_test)
# y_train = y_train.reshape((-1,1))
# lr = LinearRegression_(x_train, y_train)
# lr.train()
# print(lr.predict(x_test))
# print(y_test)
lr = LinearRegression()
lr.fit(x_train, y_train, alpha=0.01, num_iters=500)
y_pre = lr.predict(x_test)
print("开始损失和结束损失", lr.cost_hist[0], lr.cost_hist[-1])
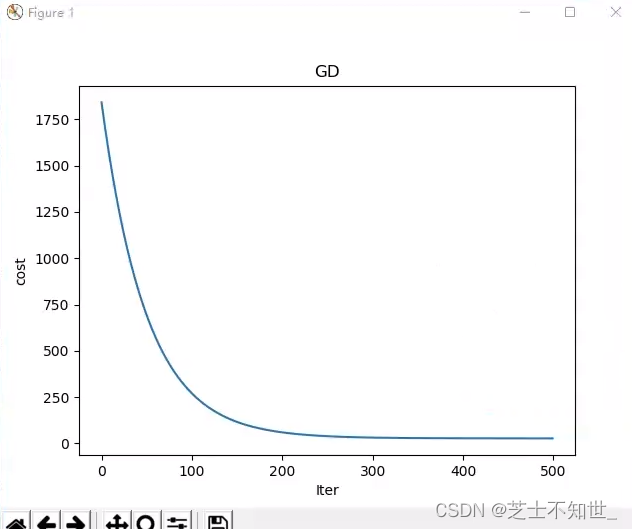
# iters-cost curve
# plt.plot(range(len(lr.cost_hist)), lr.cost_hist)
# plt.xlabel('Iter')
# plt.ylabel('cost')
# plt.title('GD')
# plt.show()
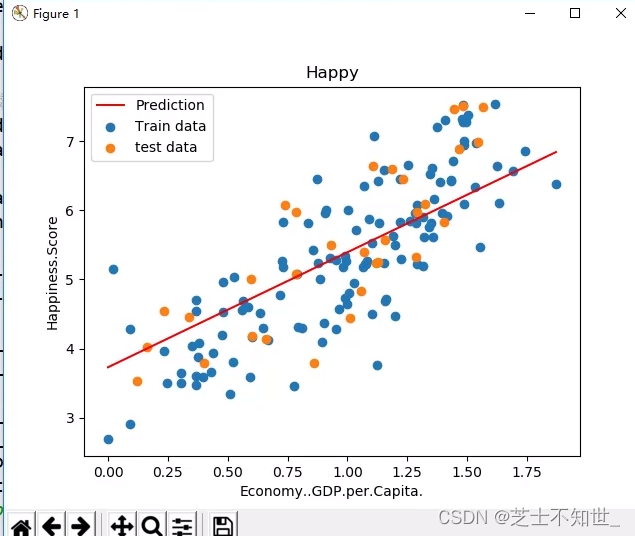
plt.scatter(x_train, y_train, label='Train data')
plt.scatter(x_test, y_test, label='test data')
plt.plot(x_test, y_pre, 'r', label='Prediction')
plt.xlabel(input_param_name)
plt.ylabel(output_params_name)
plt.title('Happy')
plt.legend()
plt.show()
多输入变量线性回归
y
=
∑
i
=
1
n
θ
i
x
i
+
b
y=\sum_{i=1}^{n} \theta^ix^i+b
y=i=1∑nθixi+b
非线性回归
1.对原始数据做非线性变换,如
x
−
>
l
n
(
x
)
x->ln(x)
x−>ln(x)
2.设置回归函数的复杂度最高
x
n
x^n
xn
2.分类模型评估(Mnist实战SGD_Classifier)
2.1 K折交叉验证K-fold cross validation
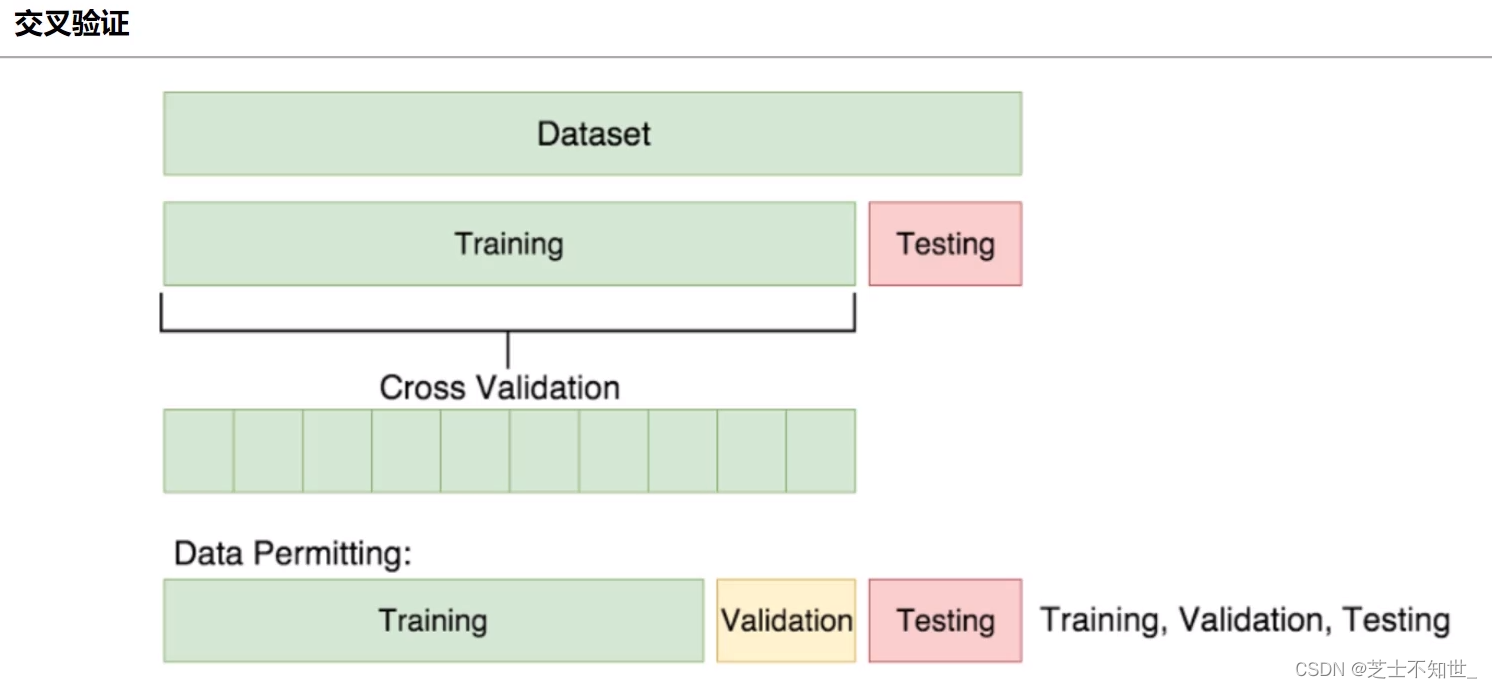
①切分完训练集training和测试集testing后
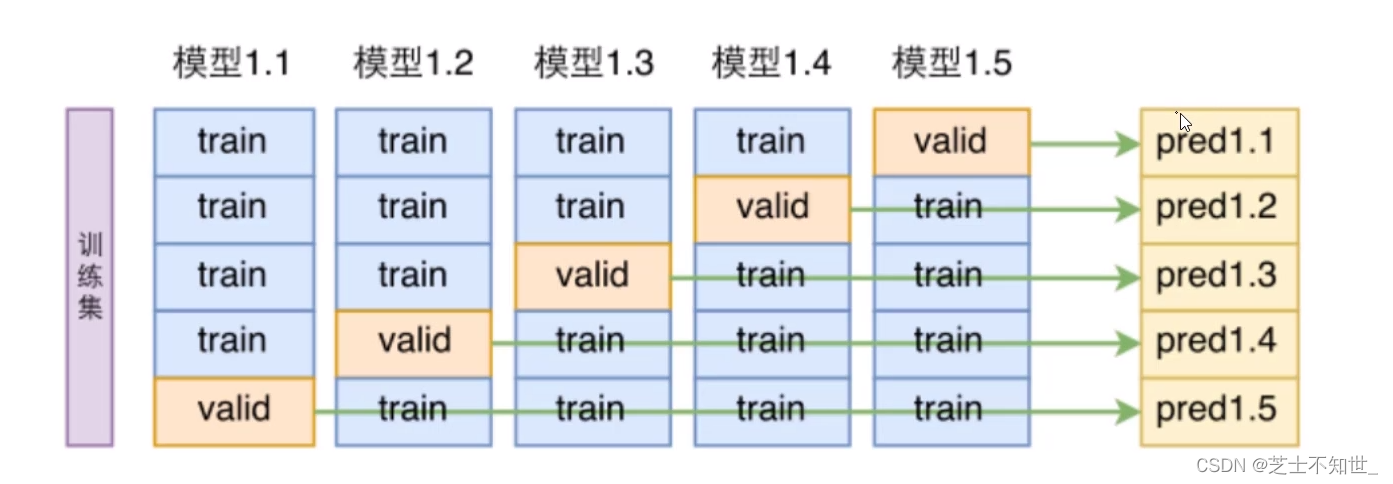
②再对training进行均分为K份
③训练的迭代将进行K轮,每轮将其中K-1份作为training,1份作为验证机validation,边训练train边验证valid
④最后训练和验证的epoch结束了,再用测试集testing进行测试。
常用的K=5/10
import numpy as np
import os
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
# from sklearn.datasets import fetch_openml
# mnist = fetch_openml('MNIST original')
# 也可以GitHub下载,手动加载
import scipy.io
mnist = scipy.io.loadmat('MNIST-original')
# 图像数据 (28x28x1)的灰度图,每张图像有784个像素点(=28x28x1)
# print(mnist) # 字典key=data和label,数据存在对应的value中
X, y = mnist['data'], mnist['label']
# print(X.shape) # data 784 x 70000,每列相当于一张图,共70000张图像
# print(y.shape) # label 1 x 70000,共70000个标签
# 划分数据,训练集training,测试集testing,train取前60000,test取后10000
# 列切片
X_train, X_test, y_train, y_test = X[:, :60000], X[..., 60000:], y[:, :60000], y[..., 60000:]
# 训练集数据洗牌打乱
import numpy as np
X_train = np.random.permutation(X_train)
y_train = np.random.permutation(y_train)
# 因为后面要画混淆矩阵,最好是2分类任务:0-10的数字判断是不是5
# 将label变为true和false
y_train_5 = (y_train == 5)[0]
y_test_5 = (y_test == 5)[0]
# print(X_train.shape)
# print(y_train_5.shape)
X_train = X_train.T
X_test = X_test.T
# 创建线性模型SGDClassifier
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter=50, random_state=42)
# sgd_clf.fit(X_train, y_train_5) # 训练
# print(sgd_clf.predict(X_test))
# K折交叉验证 划分训练集training,验证集validation,并训练
# 方法一:
from sklearn.model_selection import cross_val_score
kfold=5
acc=cross_val_score(sgd_clf, X_train, y_train_5, cv=kfold, scoring='accuracy') ## cv是折数
avg_acc = sum(acc) / kfold
print("avg_acc=", avg_acc)
# 返回每折的acc:[0.87558333 0.95766667 0.86525 0.91483333 0.94425]
# 方法二
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone # K折中每折训练时,模型带有相同参数
kfold = 5
acc = []
skfold = StratifiedKFold(n_splits=kfold, random_state=42)
i = 1
for train_idx, test_idx in skfold.split(X_train, y_train_5):
# 克隆模型
clone_clf = clone(sgd_clf)
# 划分训练集training和验证集validation
X_train_folds = X_train[train_idx]
X_val_folds = X_train[test_idx]
y_train_folds = y_train_5[train_idx]
y_val_folds = y_train_5[test_idx]
# 模型训练
clone_clf.fit(X_train_folds, y_train_folds)
# 对每折进行预测,计算acc
y_pred = clone_clf.predict(X_val_folds)
n_correct = sum(y_pred == y_val_folds)
acc.append(n_correct / len(y_pred))
print("Split", i, "/", kfold, "Done.")
i = i + 1
# 平均acc
avg_acc = sum(acc) / kfold
print("avg_acc=", avg_acc)
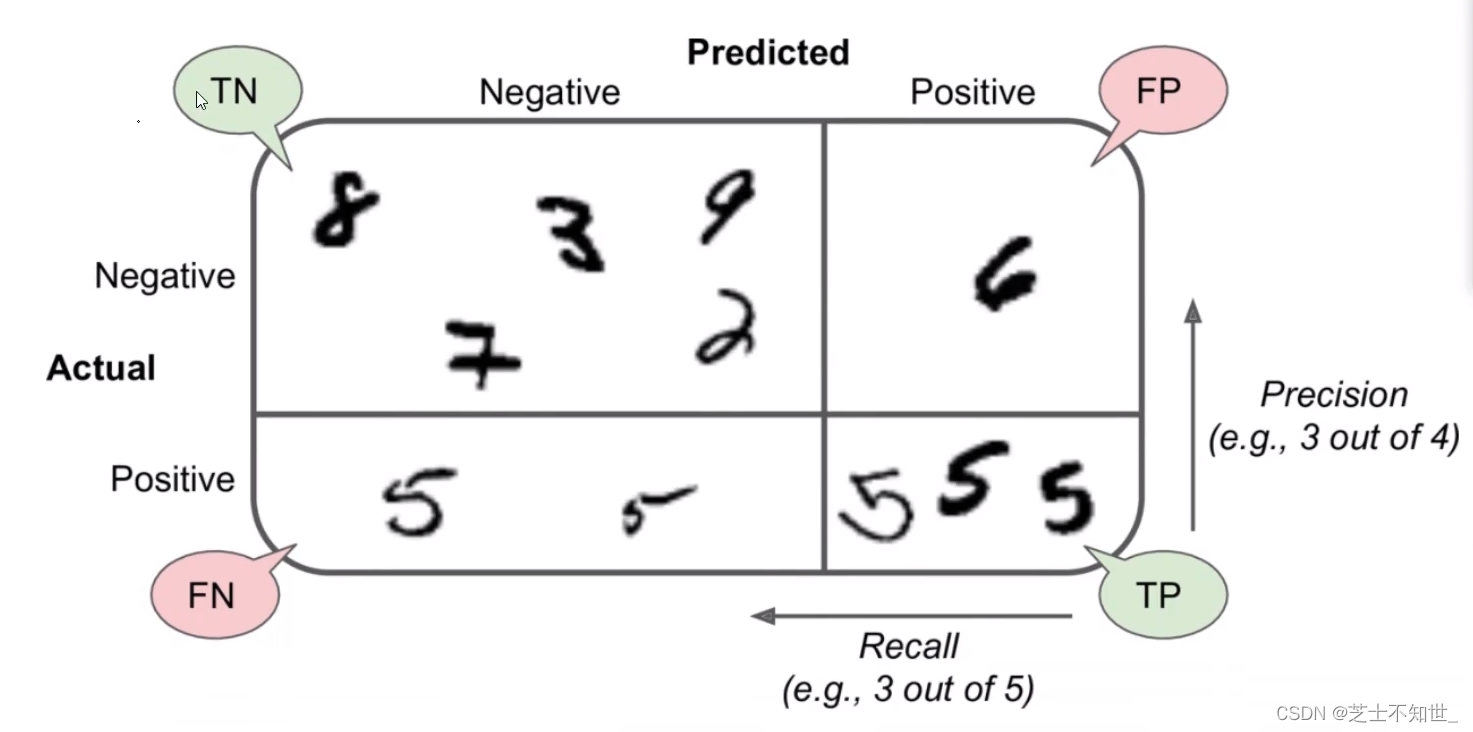
2.2 混淆矩阵Confusion Matrix
分类任务,下例对100人进行男女二分类,100中,模型检测有50人为男(实际全为男),50人为女(实际20为女 30为男)。

一个完美的分类是只有主对角线非0,其他都是0
n分类:混淆矩阵就是nxn

接上个代码
from sklearn.model_selection import cross_val_predict
# 60000个数据,进行5折交叉验证
# cross_val_predict返回每折预测的结果的concat,每折12000个结果,5折共60000个结果
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=kfold)
# 画混淆矩阵
from sklearn.metrics import confusion_matrix
confusion=confusion_matrix(y_train_5, y_train_pred) # 传入train的标签和预测值
# 2分类的矩阵就是2x2的[[TN,FP],[FN,TP]]
plt.figure(figsize=(2, 2)) # 设置图片大小
# 1.热度图,后面是指定的颜色块,cmap可设置其他的不同颜色
plt.imshow(confusion, cmap=plt.cm.Blues)
plt.colorbar() # 右边的colorbar
# 2.设置坐标轴显示列表
indices = range(len(confusion))
classes = ['5', 'not 5']
# 第一个是迭代对象,表示坐标的显示顺序,第二个参数是坐标轴显示列表
plt.xticks(indices, classes, rotation=45) # 设置横坐标方向,rotation=45为45度倾斜
plt.yticks(indices, classes)
# 3.设置全局字体
# 在本例中,坐标轴刻度和图例均用新罗马字体['TimesNewRoman']来表示
# ['SimSun']宋体;['SimHei']黑体,有很多自己都可以设置
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 4.设置坐标轴标题、字体
# plt.ylabel('True label')
# plt.xlabel('Predicted label')
# plt.title('Confusion matrix')
plt.xlabel('预测值')
plt.ylabel('真实值')
plt.title('混淆矩阵', fontsize=12, fontfamily="SimHei") # 可设置标题大小、字体
# 5.显示数据
normalize = False
fmt = '.2f' if normalize else 'd'
thresh = confusion.max() / 2.
for i in range(len(confusion)): # 第几行
for j in range(len(confusion[i])): # 第几列
plt.text(j, i, format(confusion[i][j], fmt),
fontsize=16, # 矩阵字体大小
horizontalalignment="center", # 水平居中。
verticalalignment="center", # 垂直居中。
color="white" if confusion[i, j] > thresh else "black")
save_flg = True
# 6.保存图片
if save_flg:
plt.savefig("confusion_matrix.png")
# 7.显示
plt.show()
2.3 准确率accuracy、精度precision、召回率recall、F1
sklearn.metrics中有对应的计算函数(y_train, y_train_pred)
准确率accurcy=预测正确个数/总样本数=
T
P
+
T
N
T
P
+
T
N
+
F
P
+
F
N
\frac{TP+TN}{TP+TN+FP+FN}
TP+TN+FP+FNTP+TN
精度precision=
T
P
T
P
+
F
P
\frac{TP}{TP+FP}
TP+FPTP
召回率recall=
T
P
T
P
+
F
N
\frac{TP}{TP+FN}
TP+FNTP
F1 Score=
2
∗
T
P
2
∗
T
P
+
F
P
+
F
N
\frac{2*TP}{2*TP+FP+FN}
2∗TP+FP+FN2∗TP=
2
∗
p
r
e
c
i
s
i
o
n
∗
r
e
c
a
l
l
p
r
e
c
i
s
i
o
n
+
r
e
c
a
l
l
\frac{2*precision*recall}{precision+recall}
precision+recall2∗precision∗recall


接上面代码
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
accuracy=accuracy_score(y_train_5,y_train_pred)
precision=precision_score(y_train_5,y_train_pred)
recall=recall_score(y_train_5,y_train_pred)
f1_score=f1_score(y_train_5,y_train_pred)
print("accuracy=",accuracy)
print("precision=",precision)
print("recall=",recall)
print("f1_score",f1_score)
2.4 置信度confidence
confidence:模型对分类预测结果正确的自信程度
y_scores=cross_val_predict(sgd_clf,X_train,y_train_5,kfold,method=‘decision_function’)方法返回每个输入数据的confidence,我们可以手动设置阈值t,对预测结果进行筛选,只有confidence_score>t,才视为预测正确。
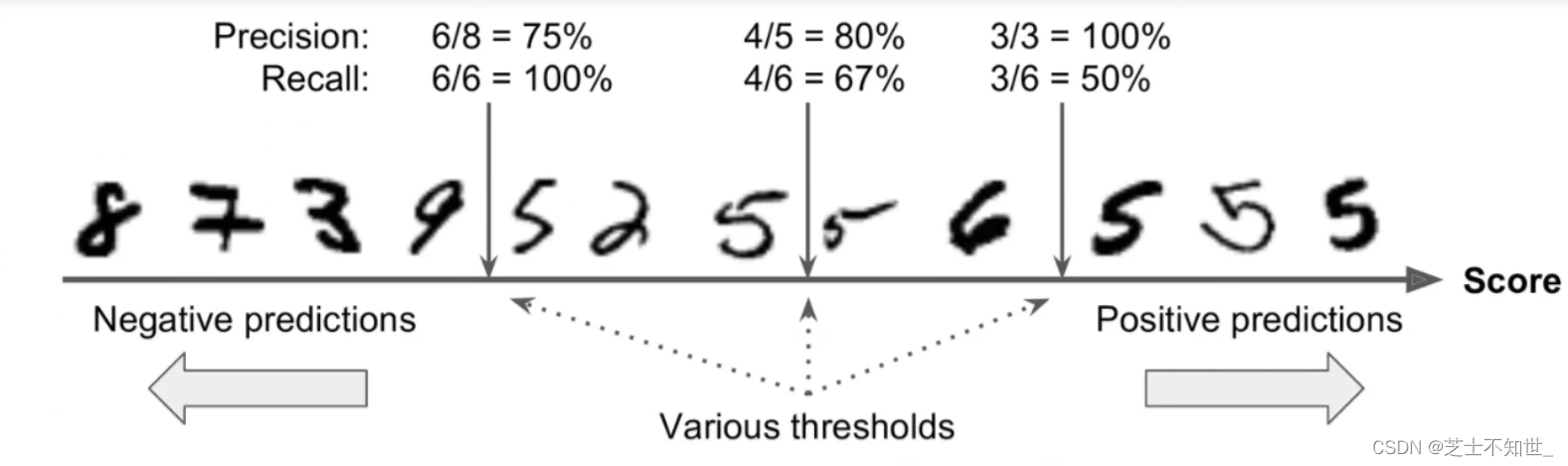
precision, recall, threshholds = precision_recall_curve(y_train_5,y_scores)函数可以自动设置多个阈值,且每个阈值都对应计算一遍precision 和 recall
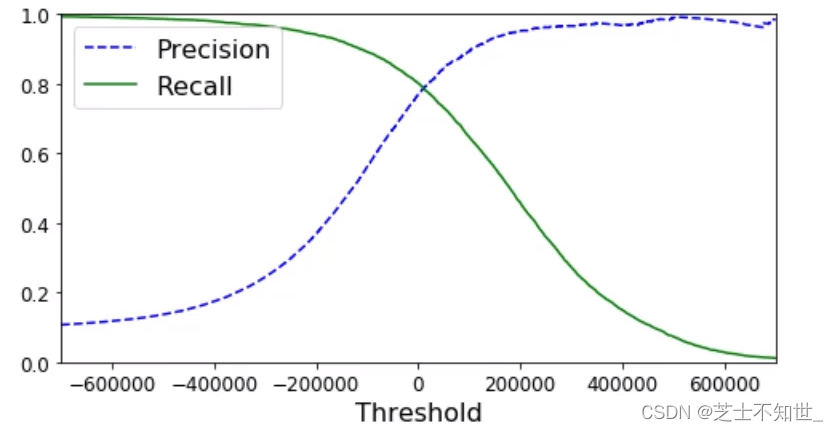
接上面代码
# 自动生成多个阈值,并计算precision, recall
y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,kfold,method='decision_function')
from sklearn.metrics import precision_recall_curve
precision, recall, threshholds = precision_recall_curve(y_train_5,y_scores)
2.5 ROC曲线
分类任务可以画出ROC曲线:理想的分类器是逼近左上直角,即曲线下方ROC AUC面积接近1.

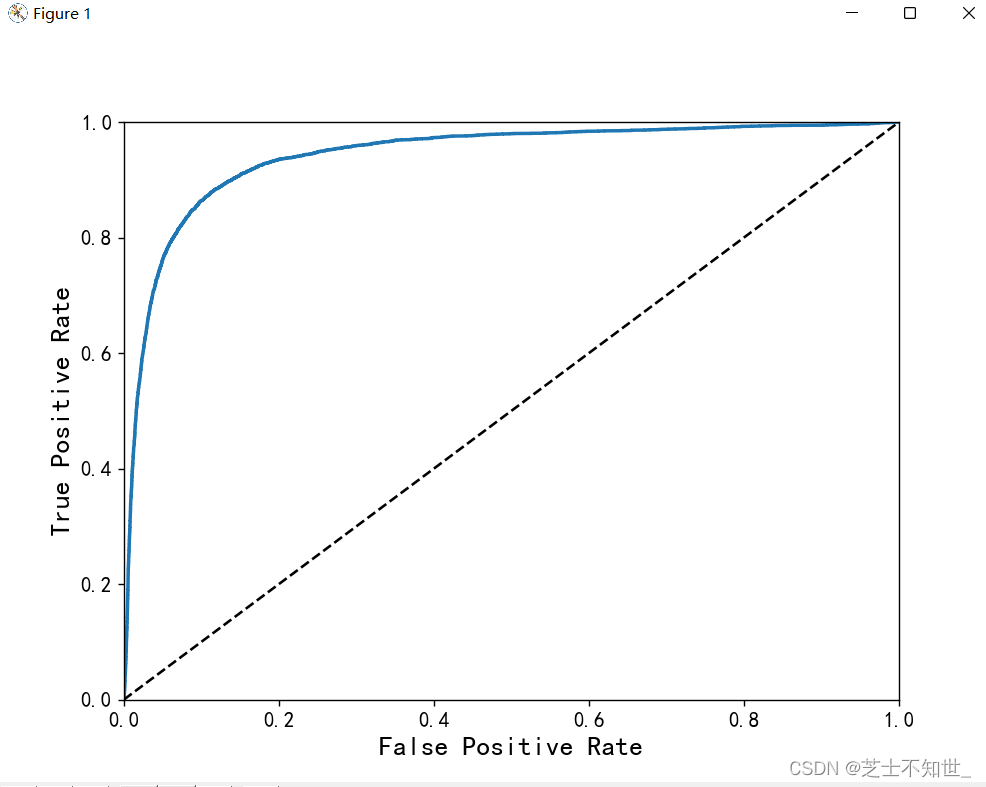
接上面代码
# 分类任务,画ROC曲线
from sklearn.metrics import roc_curve
fpr,tpr,threshholds=roc_curve(y_train_5,y_scores)
def plot_roc_curve(fpr,tpr,label=None):
plt.plot(fpr,tpr,linewidth=2,label=label)
plt.plot([0,1],[0,1],'k--')
plt.axis([0,1,0,1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8,6))
plot_roc_curve(fpr,tpr)
plt.show()
# 计算roc_auc面积
from sklearn.metrics import roc_auc_score
roc_auc_score=roc_auc_score(y_train_5,y_train_pred)
3.训练调参基本功(LinearRegression)
构建线性回归方程拟合数据点
3.1 线性回归模型实现
准备数据,预处理perprocess(标准化normalize),划分数据集(训练集train和测试集test),导包(sklearn或自己写的class),实例化LinearRegression,设置超参数(lr/eopch/batch…),是否制定learning策略(学习率衰减策略),权重参数初始化init_weight(随机初始化/迁移学习),训练(fit或自己写for迭代计算梯度更新参数),预测
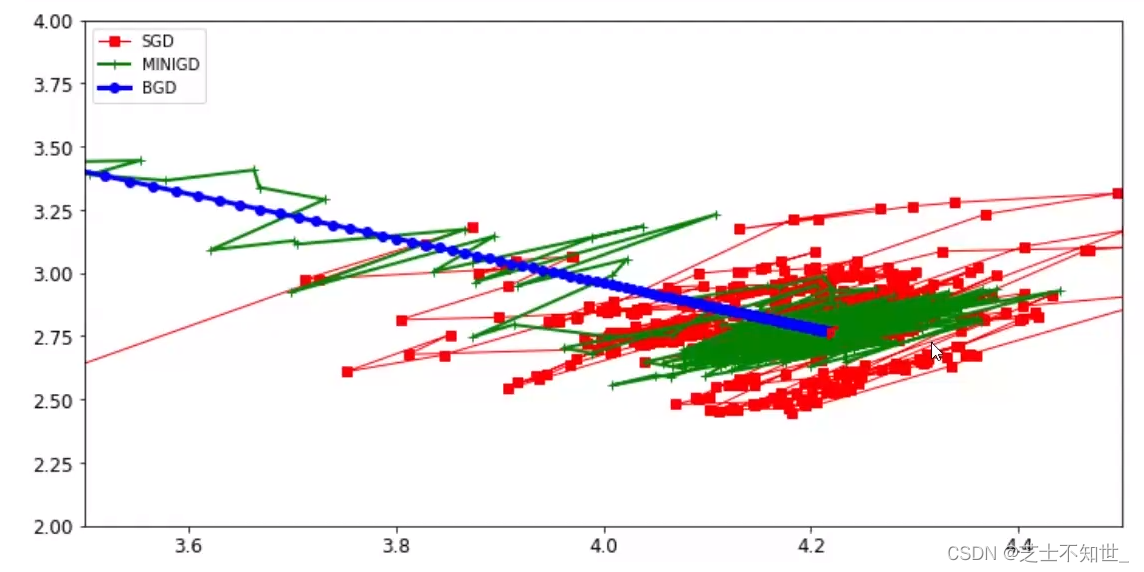
3.2不同GD策略对比




![[GUET-CTF2019]re](https://img-blog.csdnimg.cn/cc3544bee5a24d09b9d077870161a868.png)