第五章 数组和广义表

1-数组定义

2-数组的顺序表示

二维数组有两种存储方式：
（1）以行序为主序
（2）以列序为主序

3-矩阵的压缩存储

（1）对称矩阵和三角矩阵

存储上三角或下三角

（2）对角矩阵

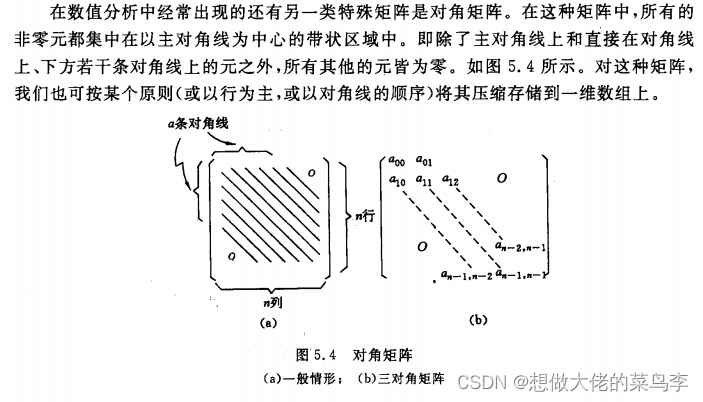
（3）稀疏矩阵

用三元组存储

存储三元组的三种方法
（1）以顺序存储结构表示三元组

（2）行逻辑链接的顺序表

（3）十字链表

4-广义表的定义

线性表的推广，也被称为列表


头尾链表的存储结构

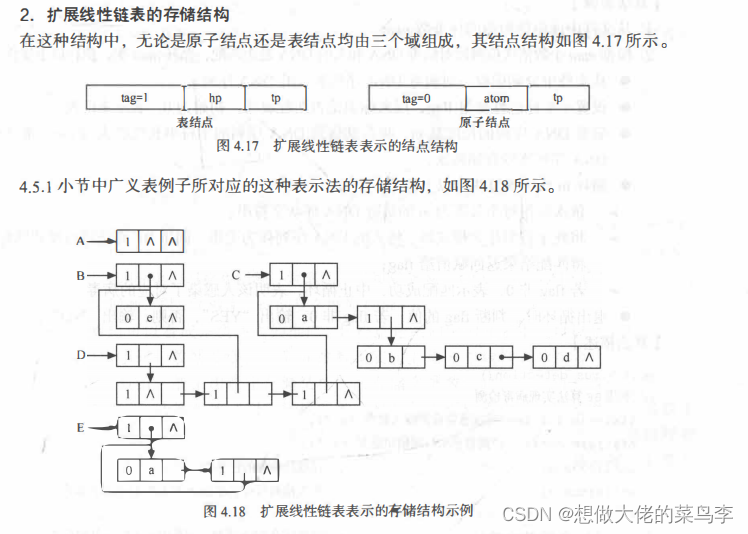
串、数组、广义表小结

串

数组

广义表

第六章 树与二叉树

在数据的逻辑结构中，非线性结构包括树结构和图结构

1-树结构中的一些基本术语

2- 二叉树的定义

注意：二叉树的子树有左右之分

3-二叉树的性质

（1）单层节点数

（2）总结点数

（3）一个重要性质

（4）满二叉树

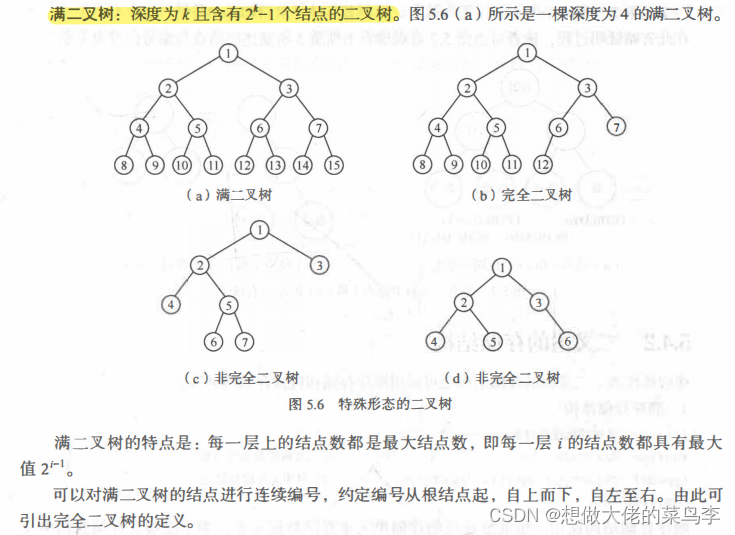
（5）完全二叉树

完全二叉树的深度问题

完全二叉树编号之间的关系

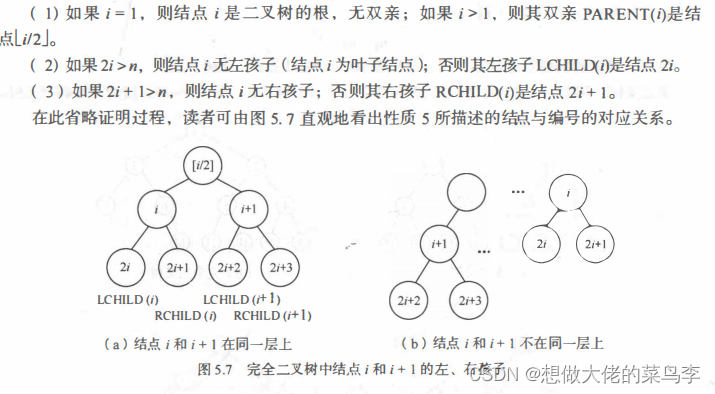
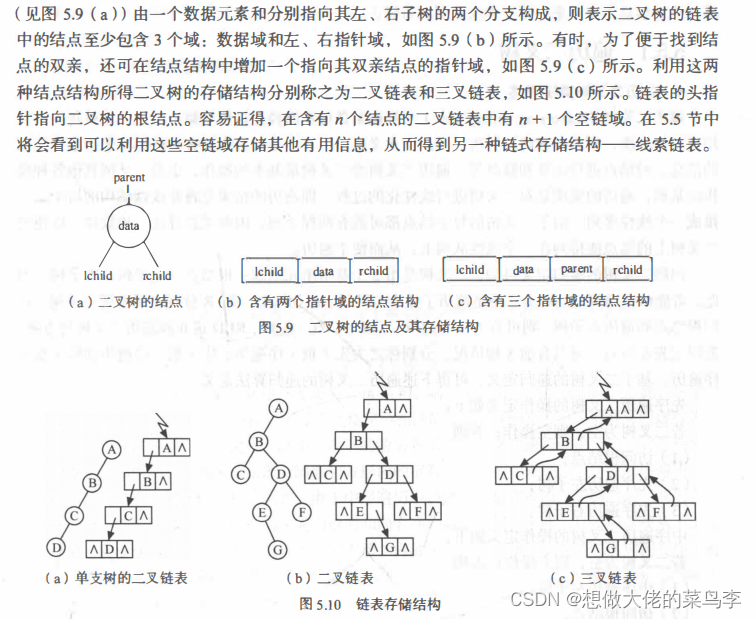
4-二叉树的存储结构

包括顺序存储和链式存储

5-遍历二叉树

（1）先序遍历

根左右

（2）中序遍历

左根右

（3）后序遍历

左右根

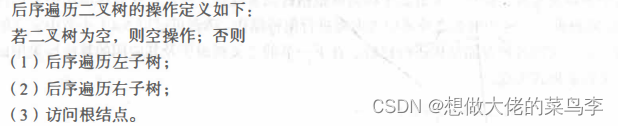
波兰式：表达式的前缀表达式
逆波兰式：表达式的后缀表达式

时间复杂度和空间复杂度

二叉树遍历算法的应用

（1）先序遍历的顺序建立二叉链表
（2）复制二叉树
（3）计算二叉树的深度
（4）统计二叉树中结点的个数

6-根据遍历序列确定二叉树

唯一确定二叉树：
（1）先序序列+中序序列
（2）后序序列+中序序列

7-线索二叉树

目的：二叉链表只能找到结点的左右孩子信息，不能直接得到节点在任意序列的前驱和后继的信息，因此在线索二叉树中增加两个指针域存放在遍历时得到的有关前驱和后继的信息

标志域为0时指向孩子；标志域为1时：左指针域指向前驱，右指针域指向后继

8-树和森林

8-1树的存储结构

树的存储结构包括：（1）双亲表示法。（2）孩子表示法。（3）孩子兄弟表示法。

（1）双亲表示法

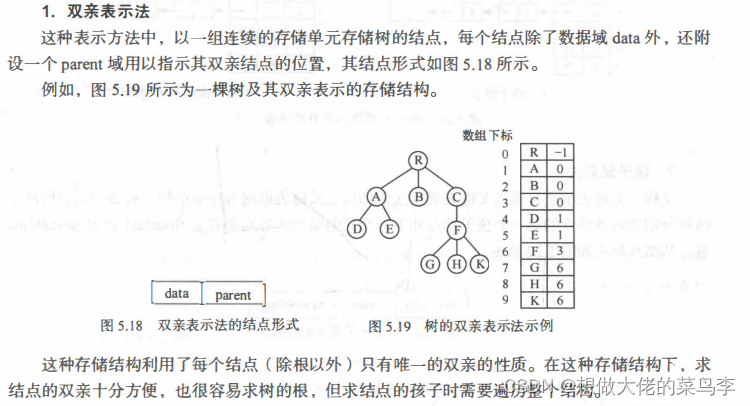
（2）孩子表示法

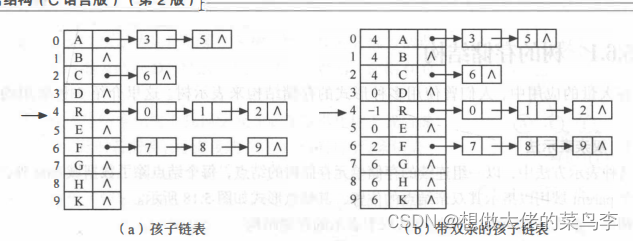
（4）孩子兄弟表示法

两个指针域：左指针域代表该节点的第一个孩子结点，右指针域代表下一个兄弟。

8-2 森林与二叉树的转换

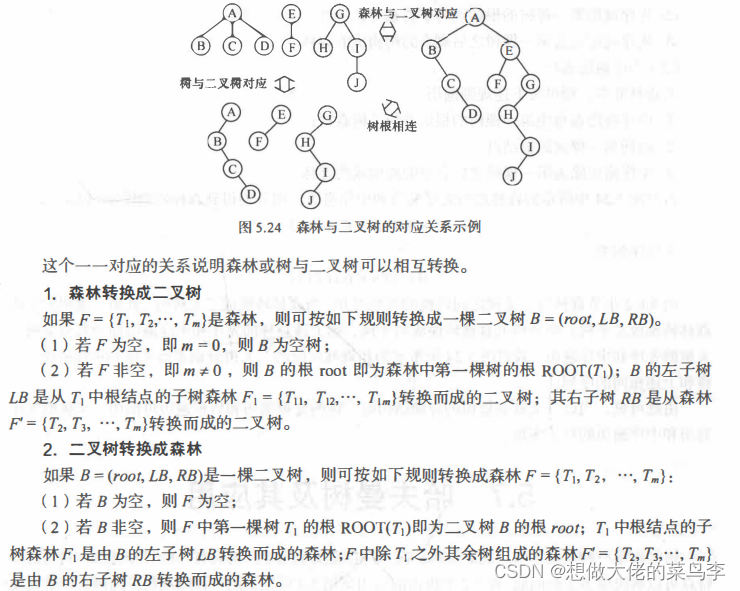
8-3 树和森林的遍历

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后跟遍历	中序遍历	中序遍历

8-4哈夫曼树（最优树）

（1）基本概念

（2）哈夫曼树的构造

（3）哈夫曼树编码

前缀编码

哈夫曼编码

哈夫曼编码满足的性质

文件的编码和译码

数和二叉树小结