各位CSDN的uu们你们好呀，今天，小雅兰的内容是高阶导数，在这之前，我们学习了导数的概念和函数的求导法则，那么今天，就让我们一起进入高阶导数的世界吧

---

一、高阶导数的定义

二、高阶导数的计算

              1.直接法

              2.间接法

---

一、高阶导数的定义

 一阶导数的导数称为二阶导数，二阶以上的导数可由归纳法逐阶定义。二阶和二阶以上的导数统称为高阶导数。从概念上讲，高阶导数可由一阶导数的运算规则逐阶计算，但从实际运算考虑这种做法是行不通的。因此有必要研究高阶导数特别是任意阶导数的计算方法。

 从概念上讲，高阶导数计算就是连续进行一阶导数的计算。因此只需根据一阶导数计算规则逐阶求导就可以了，但从实际计算角度看，却存在两个方面的问题：
（1）一是对抽象函数高阶导数计算，随着求导次数的增加，中间变量的出现次数会增多，需注意识别和区分各阶求导过程中的中间变量。
（2）二是逐阶求导对求导次数不高时是可行的，当求导次数较高或求任意阶导数时，逐阶求导实际是行不通的，此时需研究专门的方法。

 

 

 

这个C(a,b) 我们之前也说过 意思是在(a,b)内所有的连续的函数的集合 

---

 二、高阶导数的计算

 1.直接法

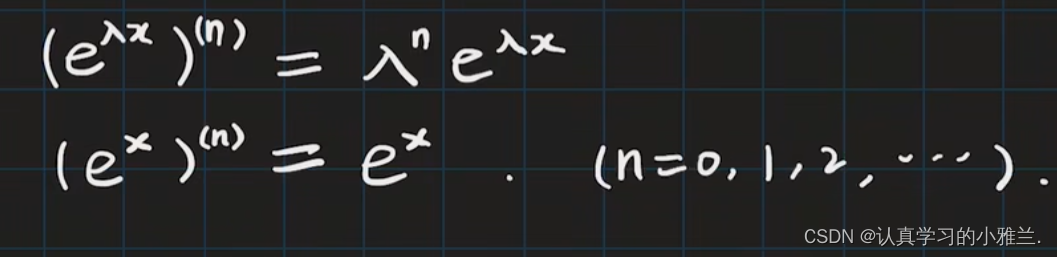
                                                                 记住！！！

 

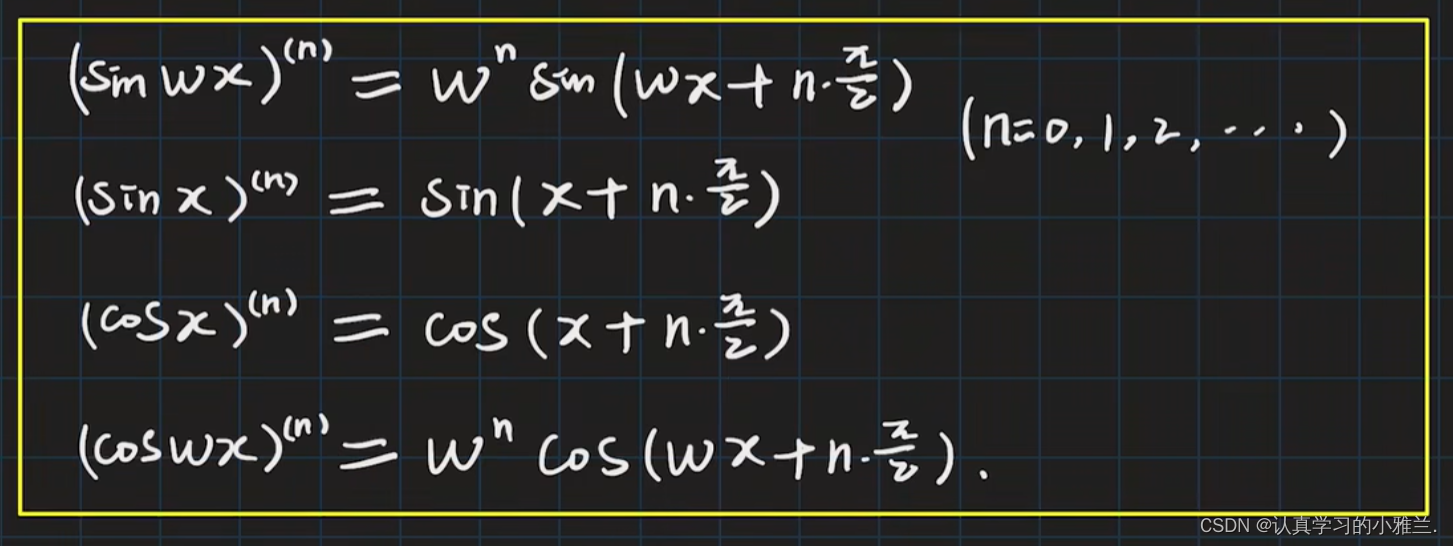
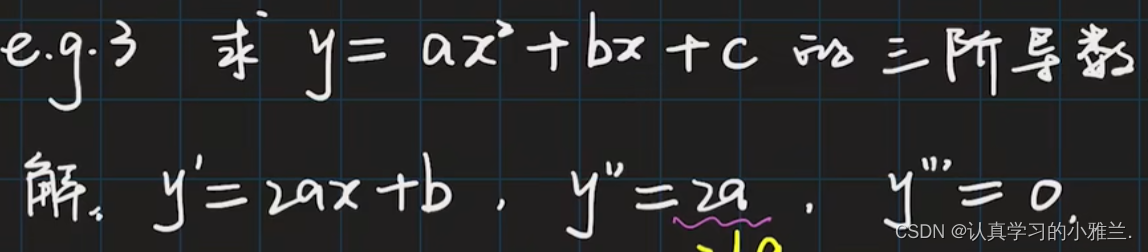
 这也是需要记住的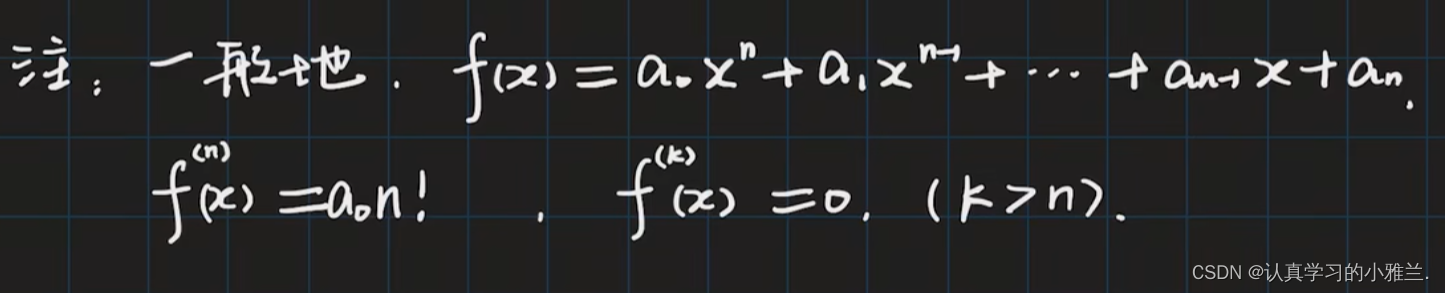

  

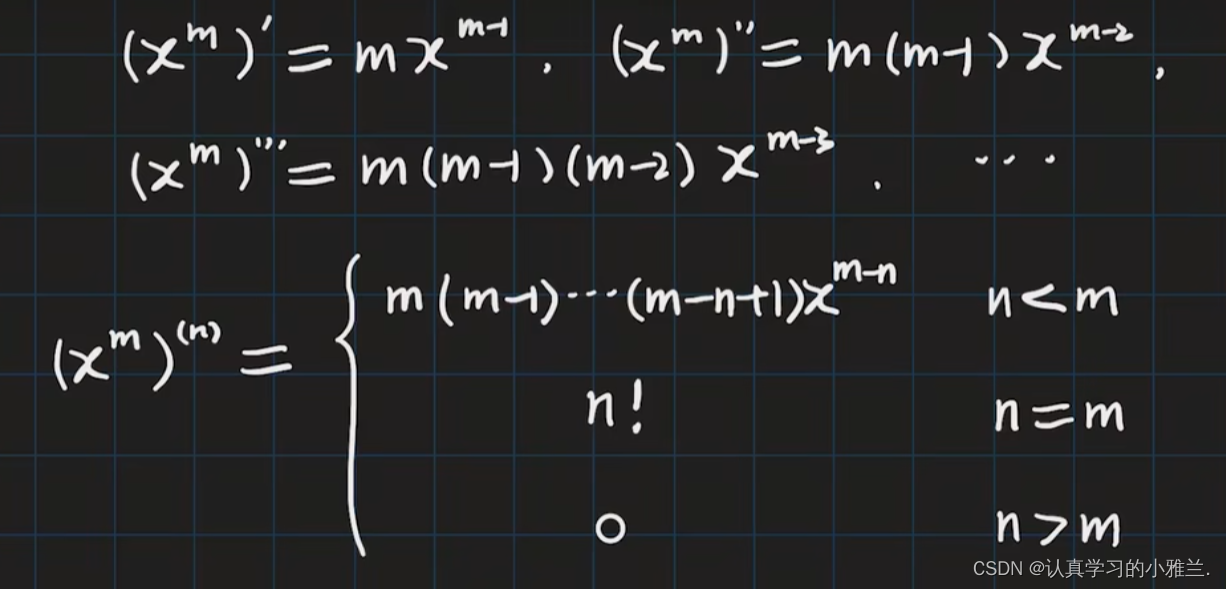
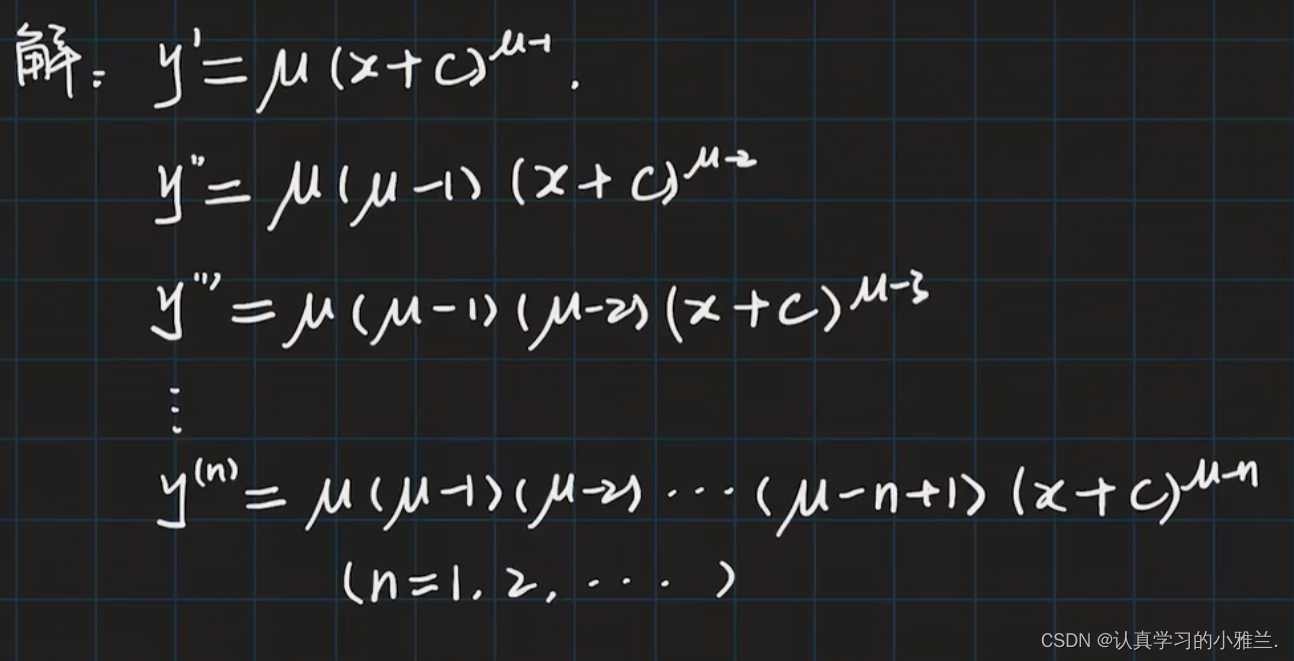
 下面，来看一下由这道例题衍生出来的常用结论

 

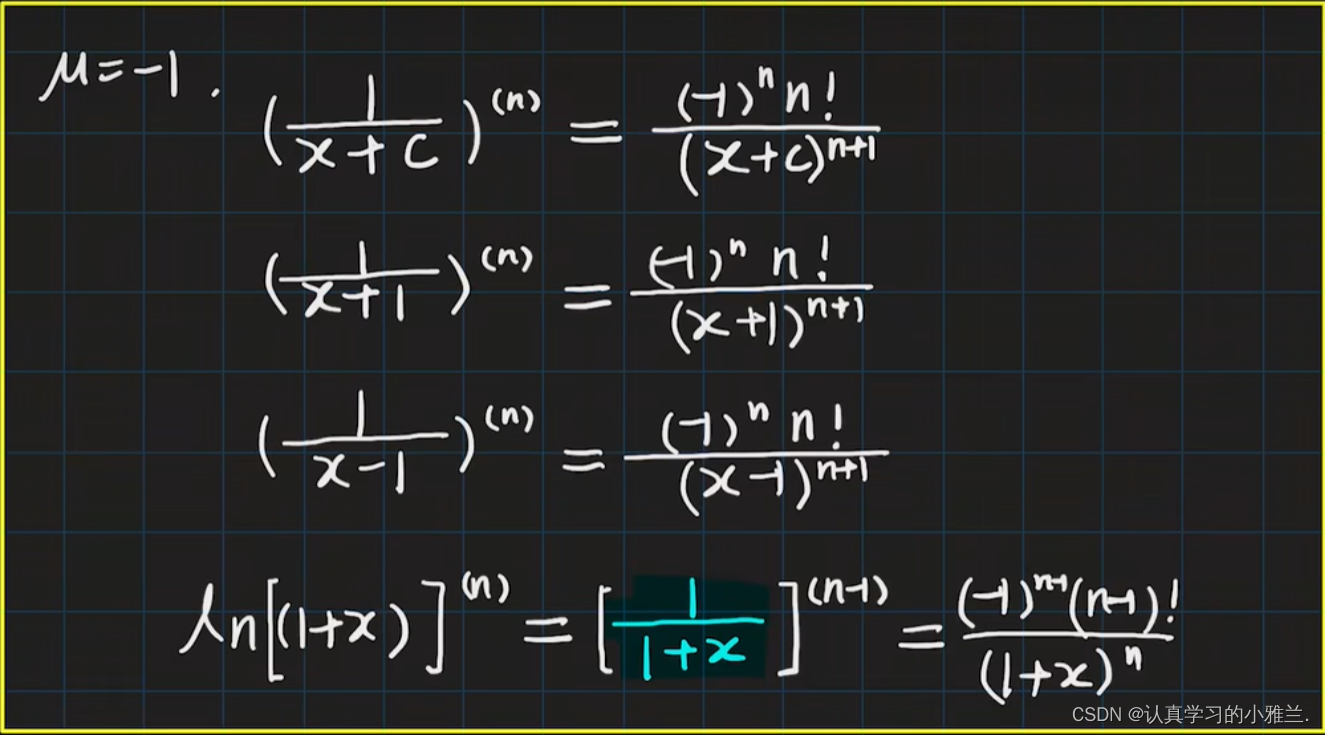
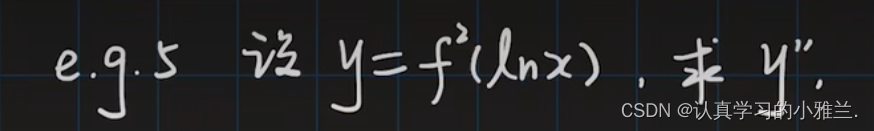
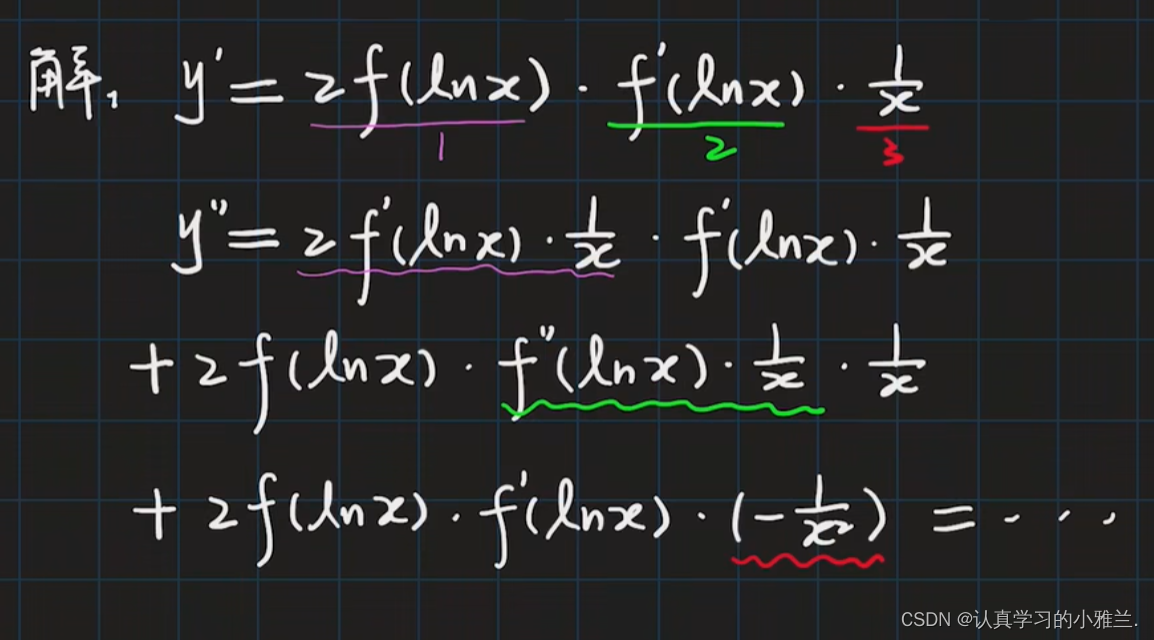
 常用高阶导数公式（记下来！！！）

---

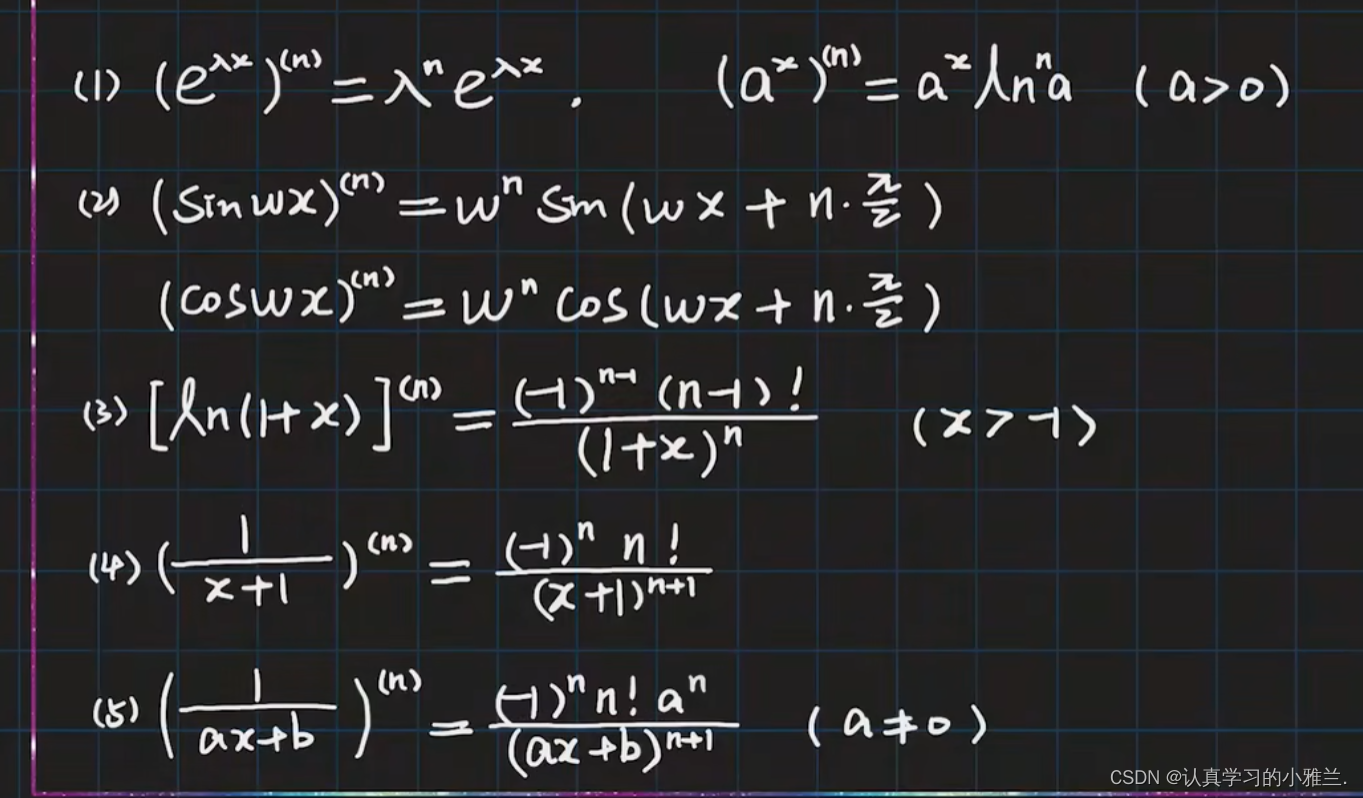
2.间接法

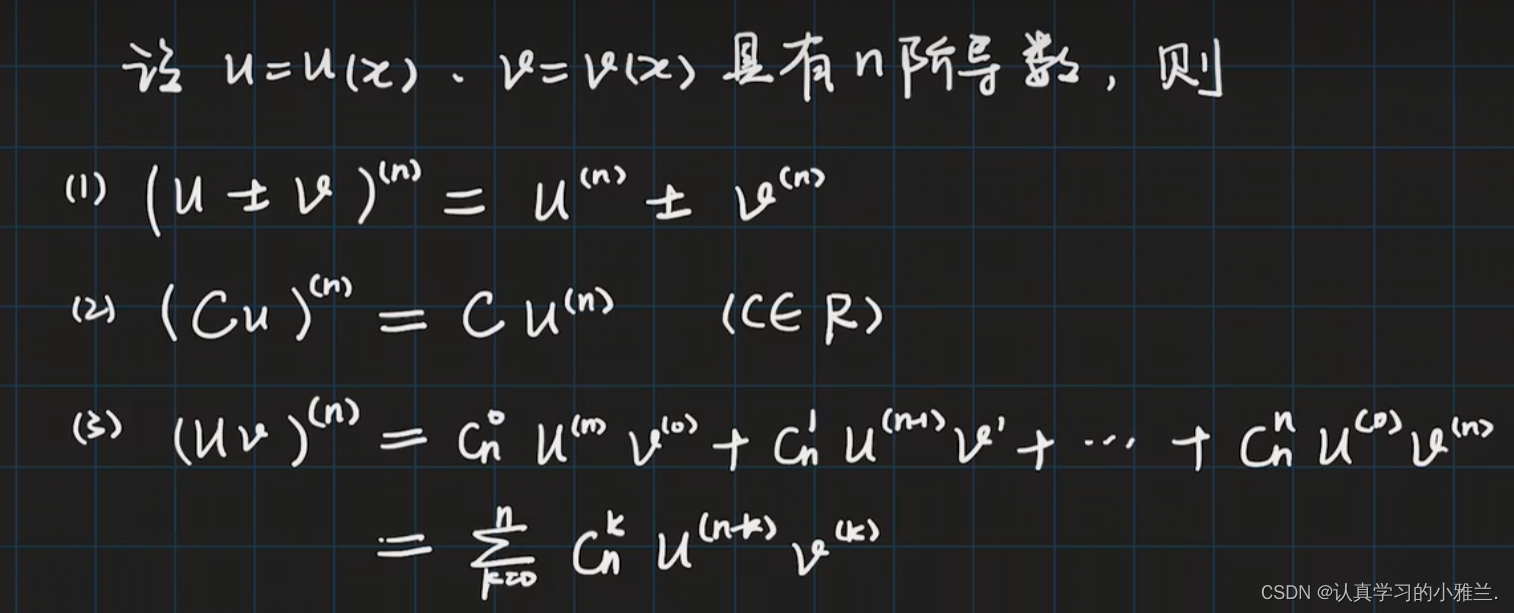
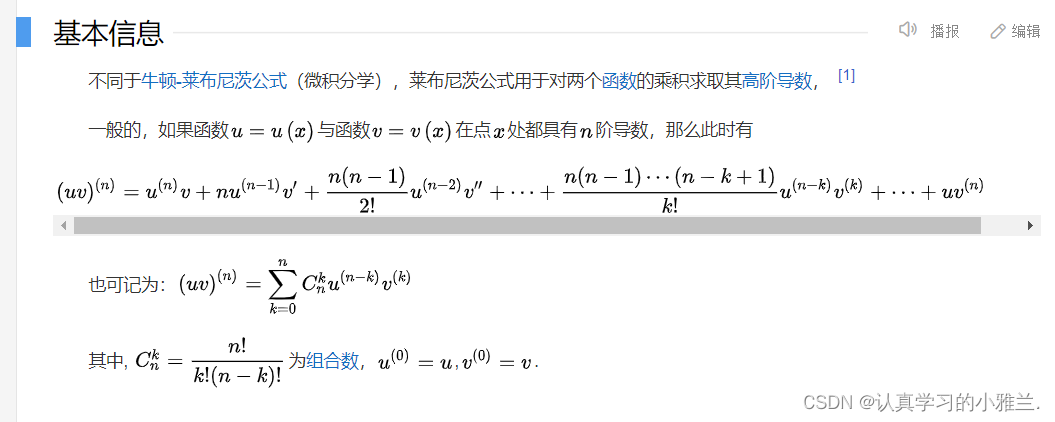
我们会发现，这与我们高中学过的二项式定理有点相似

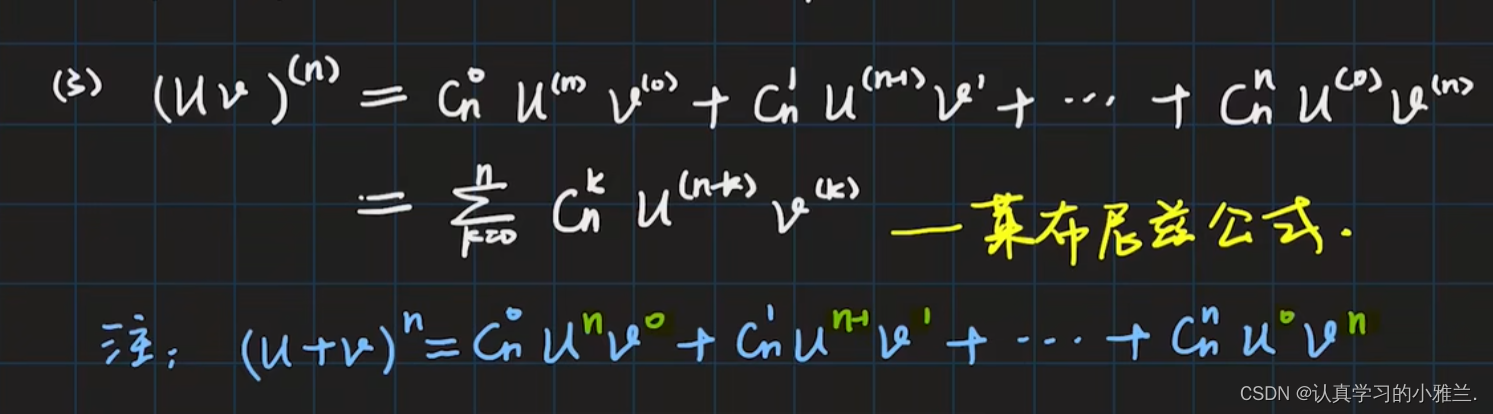二项式定理（英语：binomial theorem），又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂，即广义二项式定理。

 

 

 

 

 

 

 

 

 

下面，我们来看几道例题

 

  

 

  

 

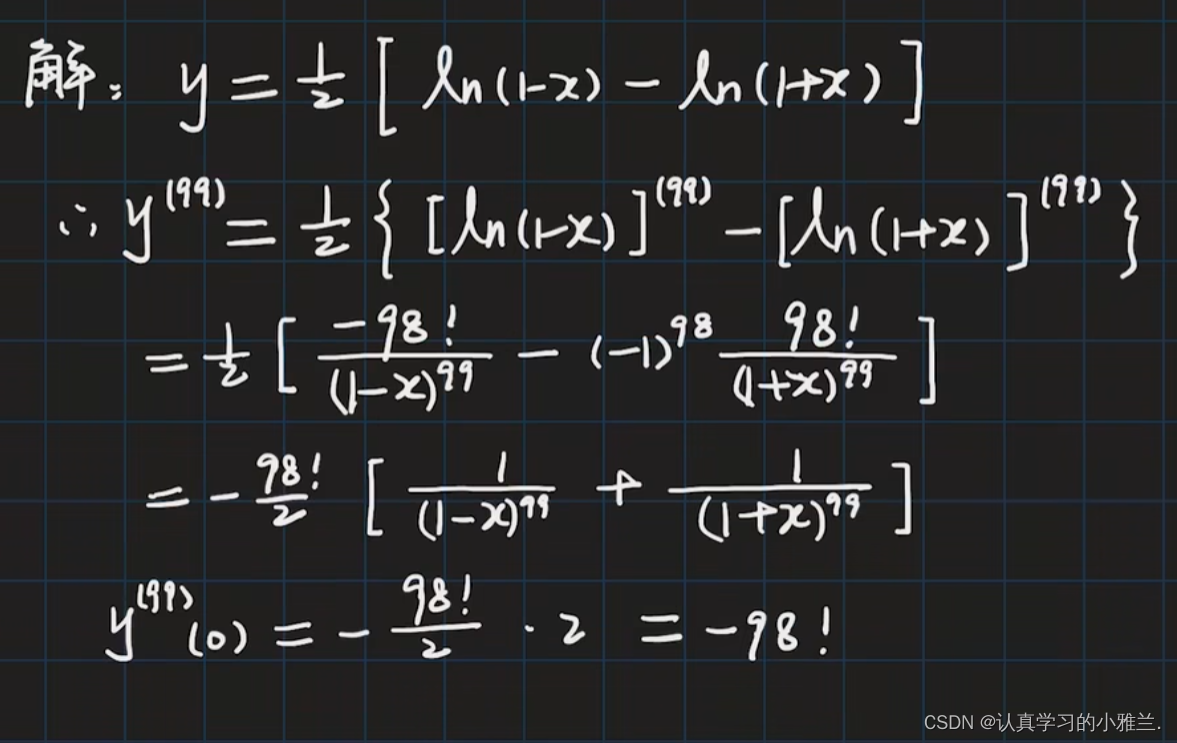
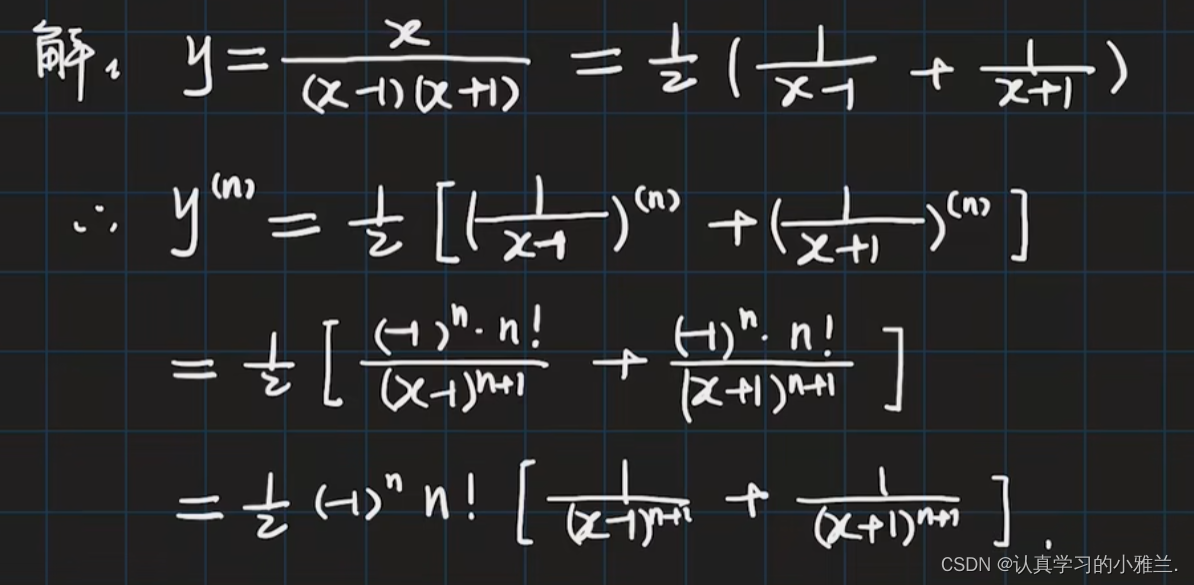
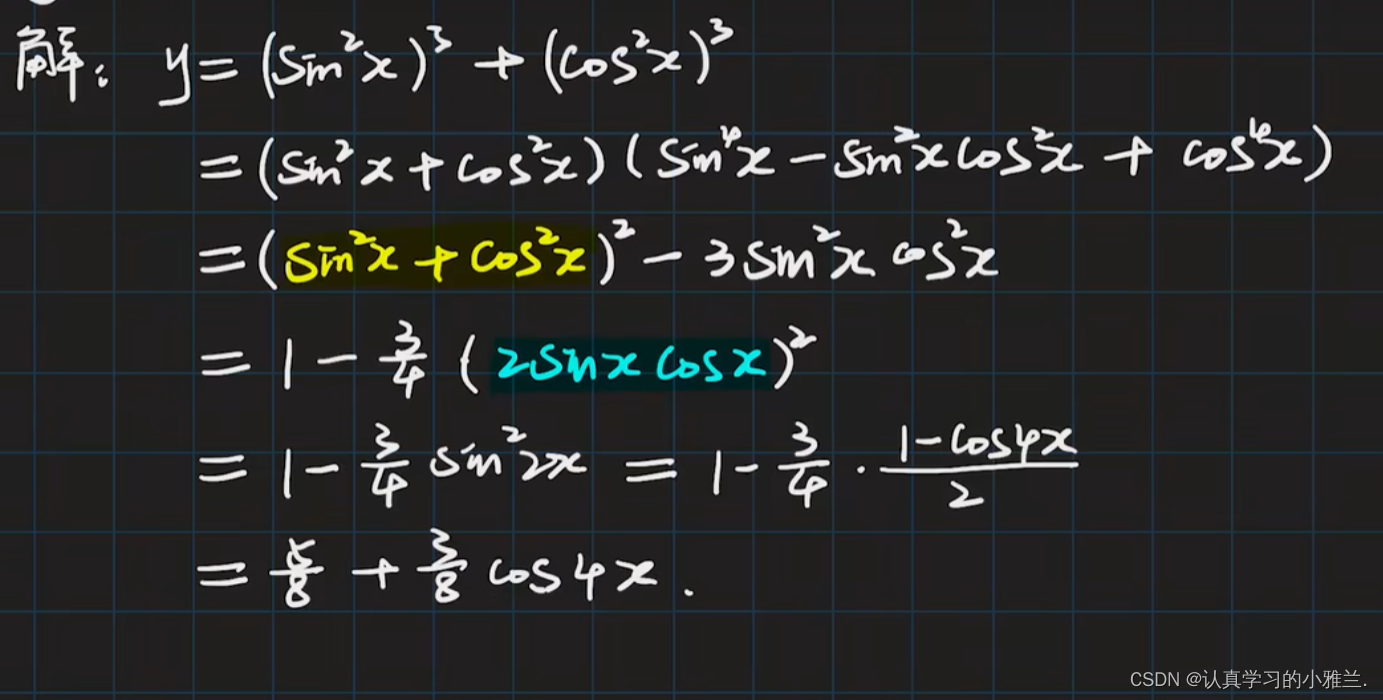
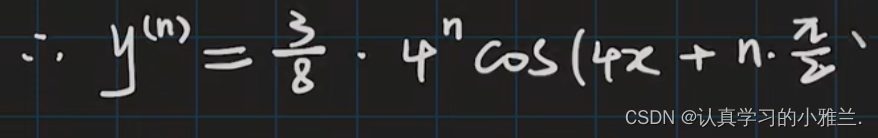
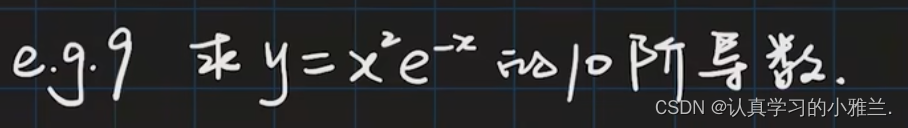
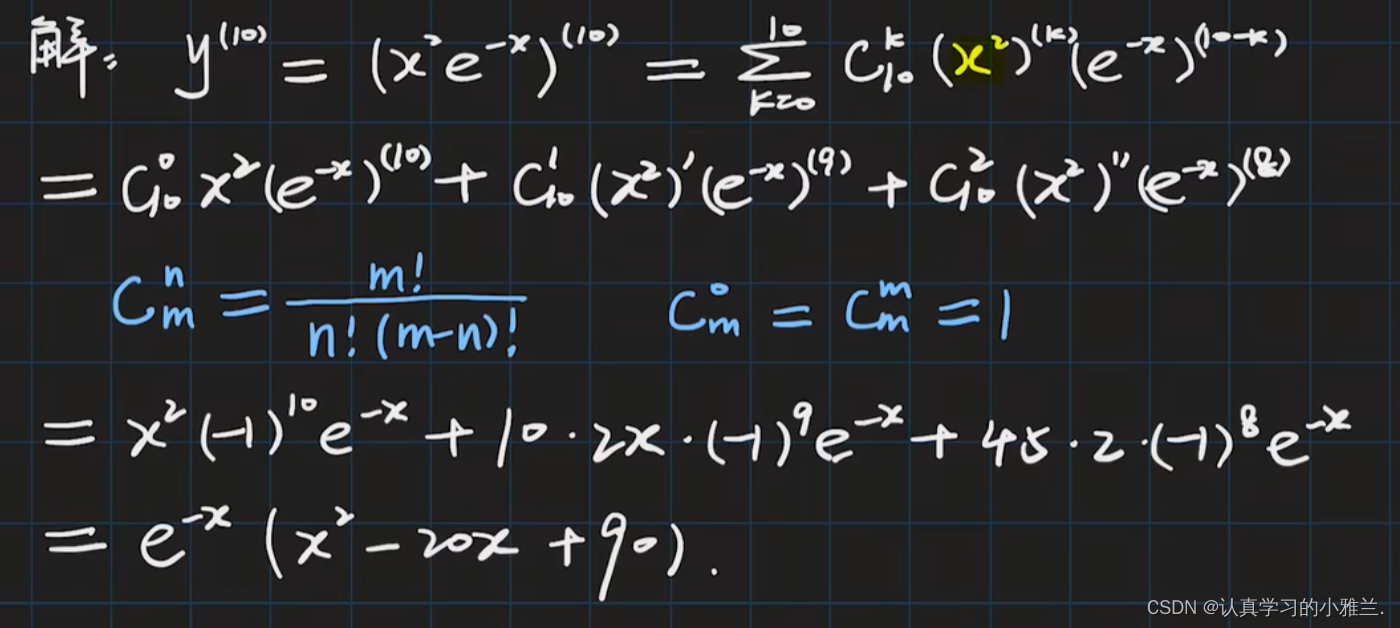 因为此函数的最高次幂为二次，所以求到二阶导数就不用再求了，它的三阶导数及之后的导数都为零

 

  

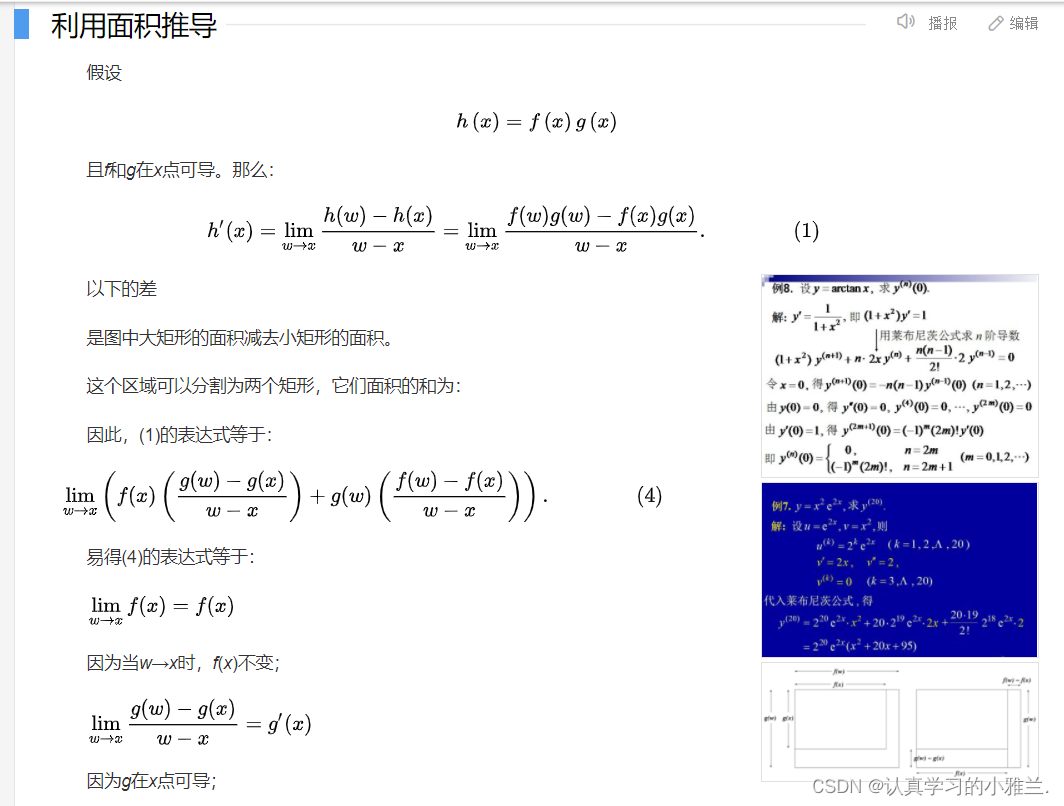
 这道题目也用了莱布尼兹公式

莱布尼茨法则，也称为乘积法则，是数学中关于两个函数的积的导数的一个计算法则。

 

 

---

小结 

---

 好啦，小雅兰今天的内容就到这里了，这篇博客主要讲解的是高阶导数，并复习了高中时期学过的二项式定理，学习了一个新的公式——莱布尼兹公式。小雅兰加油呀！！！