基于卡尔曼滤波器的PID控制系统结构如图1所示。

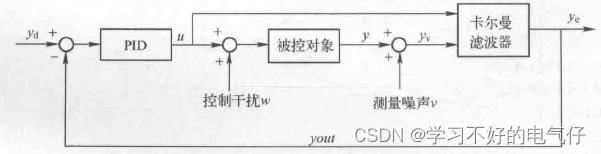
图1 基于卡尔曼滤波器的PID控制

被控对象为二阶传递函数：

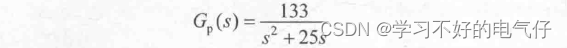
离散化结果与“基于卡尔曼滤波器的PID控制-1”的仿真实例相同。采样时间为1ms。控制干扰信号w(k)和测量噪声信号v(k)幅值均为0.002的白噪声信号，输入信号为一阶跃信号。采用卡尔曼滤波器实现信号的滤波，取 =1，R=1。仿真时间为1s。分两种情况进行仿真:M=1时为未加滤波，M=2时为加滤波。在PID控制器中，取kp=8.0 ，ki =0.80 ,kd= 0.20。加入滤波器前后PID阶跃响应如图2和图3所示，仿真结果表明，通过采用滤波器使控制效果明显改善。

本方法的不足之处是设计卡尔曼滤波器时需要被控对象的精确模型。

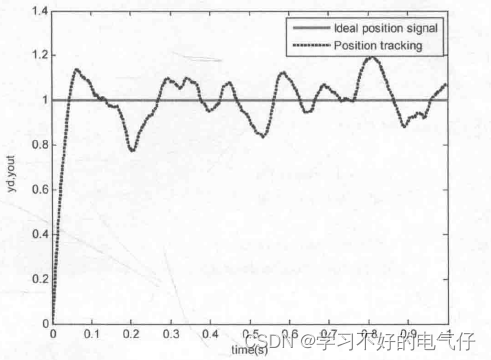
图2 无滤波器时PID控制阶跃响应（M=1）

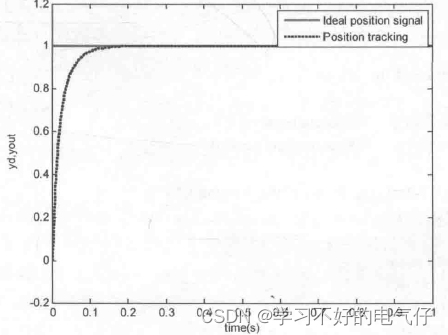
图3 加入滤波器后PID控制阶跃响应（M=2）

仿真程序：

%Discrete Kalman filter for PID control

%Reference kalman_2rank.m

%x=Ax+B(u+w(k));

%y-Cx+DHv(k)

clear all;

close all;

ts=0.001;

%Continuous Plant

a=25;b=133;

sys=tf(b,[1,a,0]);

dsys=c2d(sys,ts,'z');

[num,den]=tfdata(dsys,'v);

A1=[0 1;0 -a];

B1=[0;b];C1=[1 0];D1=[0];

[A,B.C,D]=c2dm(A1,B1,C1,D1,ts,z);

Q=1; %Covariances of w

R=1; %Covariances ofv

P=B*Q*B'; %Initial crror covariance

x=zeros(2,1); %Initial condition on the state

u_1=0;u_2=0;

y_1=0;y_2=0;

ei=0;

error_1=0;

for k=1:1:1000

time(k)=k*ts;

yd(k)=1;

kp=8.0;ki=0.80;kd=0.20;

w(k)=0.002*rands(1); %Process noise on u

v(k)=0.002*rands(1); %Measurement noise on y

y(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;yv(k)-y(k)+v(k);

%Measurement update

Mn=P*C/(C*P*C+R);

P=A*P*A'+B*Q*B';

P=(eye(2)-Mn*C)*P;

x=A*x+Mn*(yv(k)-C*A*x);

ye(k)=C*x+D;%Filtered value

M=1;

if M==1 %No kalman filter

yout(k)=yv(k);

else if M=-2 %Using kalman filter

yout(k)=ye(k);

end

error(k)=yd(k)-yout(k);

ei=ei+error(k)*ts;

u(k)=kp*error(k)+ki*ei+kd*(error(k)-error_1)ts; %PID

u(k)=u(k)+w(k);

errcov(k)=C*P*C'; %Covariance of estimation error

%Time update

x=A*x+B*u(k);

u_2=u_l;u_1=u(k);

y 2=y_1;y_1=yout(k);

error_1=error(k);

end

figure(1);

plot(time,yd,'r',time,yout,'k:',linewidth',2);

xlabel('time(s));ylabel('yd,yout');

legend('Ideal Dosition signal''Position tracking'):