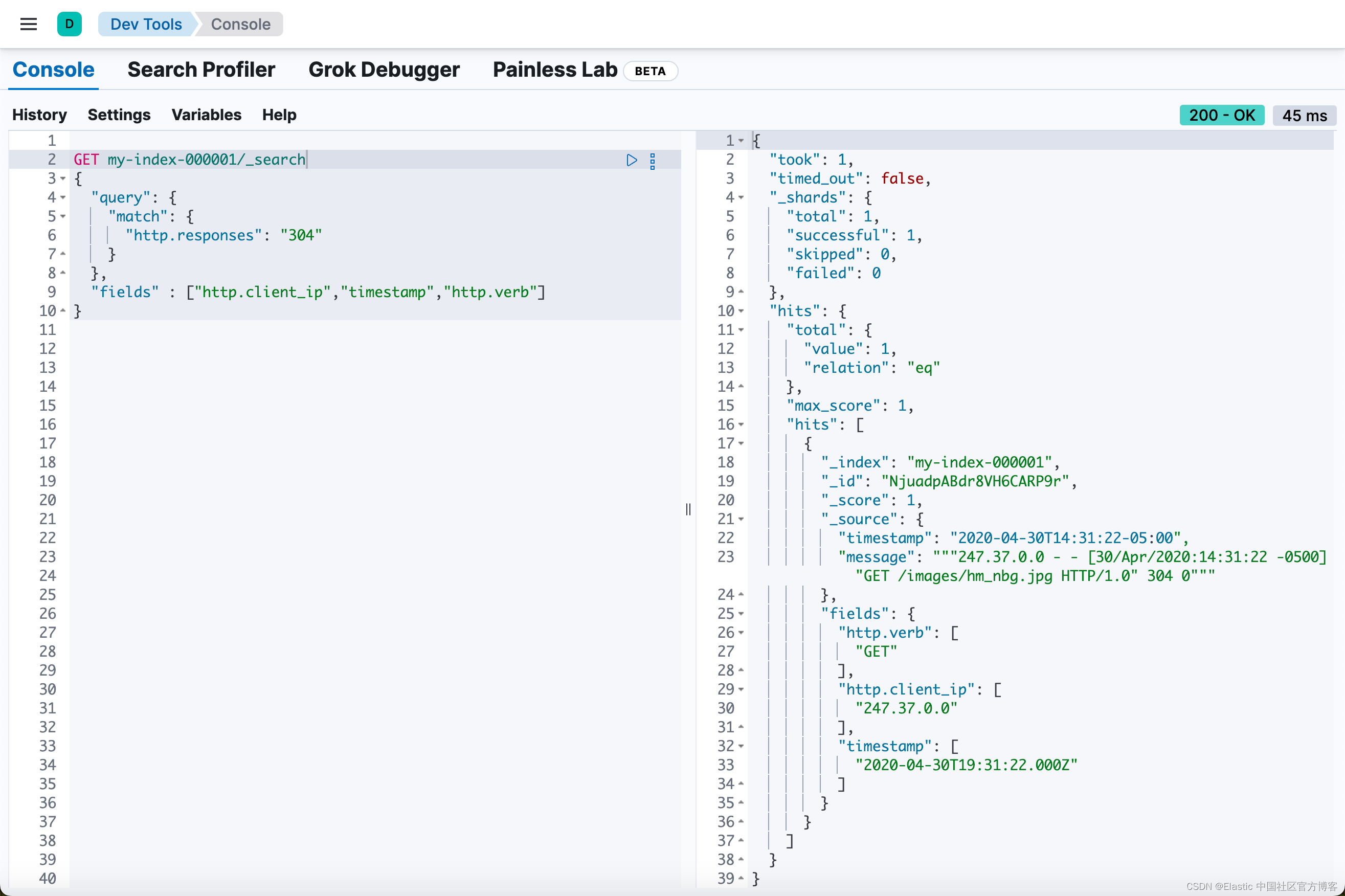
目录

A. Odd One Out

B. Not Quite Latin Square

C. Can I Square?

D. Unnatural Language Processing

E. Romantic Glasses

F. Greetings

---

A. Odd One Out

Problem - A - Codeforces

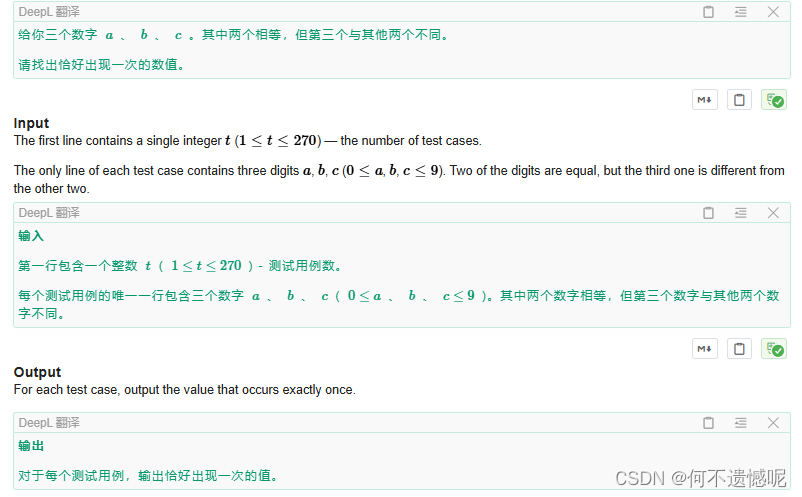
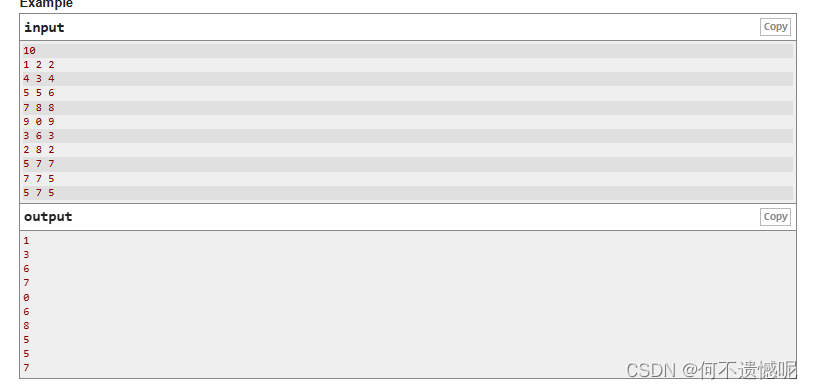
输出一个不同于其他两个数的数，用异或操作可以轻松解决。

void solve{
    int a,b,c;
    cin>>a>>b>>c;
    cout<<a^b^c<<"\n";
}

B. Not Quite Latin Square

Problem - B - Codeforces

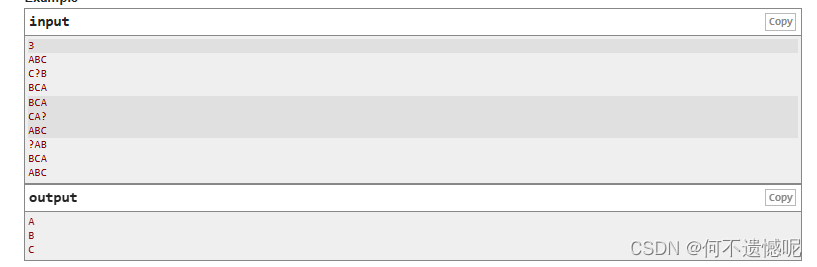
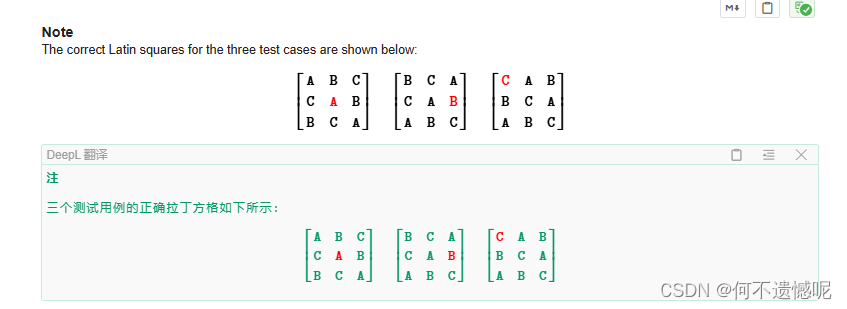
找到？的位置，再分析它这行和列出现的元素。

char a[30][30];
void solve()
{
    int x, y;
    for (int i = 1; i <= 3; i++)
    {
        for (int j = 1; j <= 3; j++)
        {
            cin >> a[i][j];
            if (a[i][j] == '?')
            {
                x = i, y = j;
            }
        }
    }
    int f[200];
    memset(f, 0, sizeof(f));
    for (int i = 1; i <= 3; i++)
    {
        f[a[x][i]]++;
        f[a[i][y]]++;
    }
    for (int i = 'A'; i <= 'C'; i++)
    {
        if (!f[i])
        {
            cout << (char)i << "\n";
        }
    }

}

C. Can I Square?

Problem - C - Codeforces

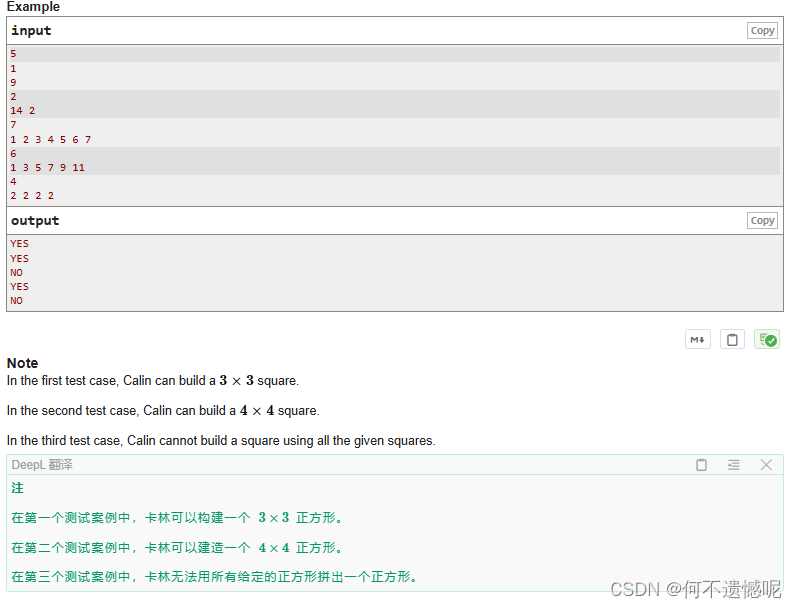
数组所有元素的和是否为完全平方数。

void solve()
{
    int n;
    cin >> n;
    ll sum = 0;
    for (int i = 1; i <= n; i++)
    {
        ll x;
        cin >> x;
        sum += x;
    }
    if ((double)sqrt(sum) == (int)sqrt(sum))
    {
        cout << "YES\n";
    }
    else cout << "NO\n";

}

D. Unnatural Language Processing

Problem - D - Codeforces

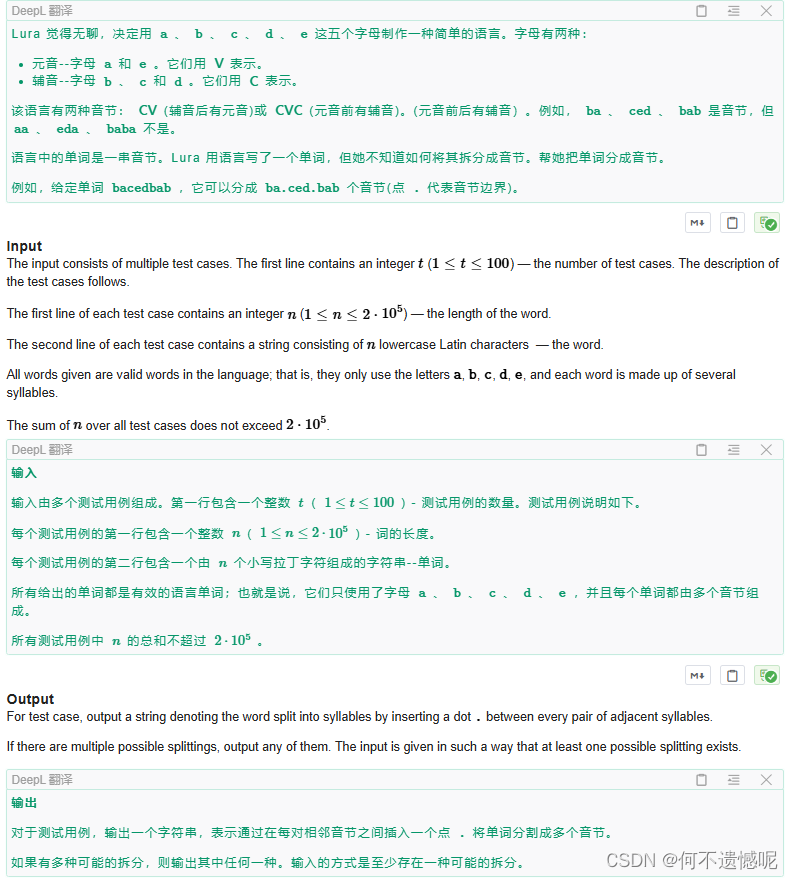
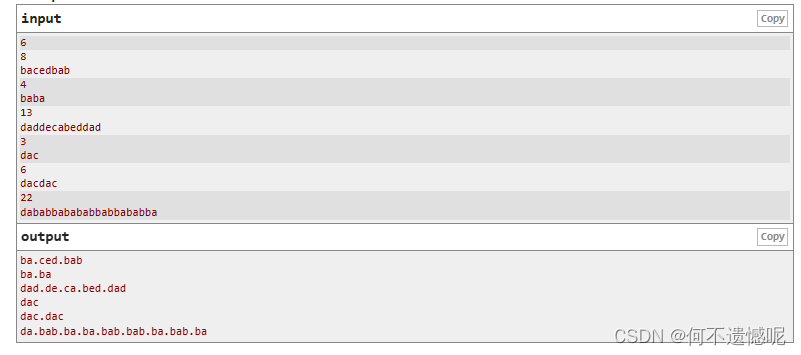
规定一个规则。

当出现CC的子串，那么它们中间必定插入一个'.'，再判断一些V后面是否插入'.'，如果V后面是CC子串则不插入，或者V位于倒数第二个元素后面也不执行插入，反之都插入。

ll pos[N];
void solve()
{
    memset(pos, 0, sizeof(pos));
    int n;
    cin >> n;
    string s,t,ans;
    t.resize(n + 1);
    cin >> s;
    for (int i = 0; i < s.size(); i++)
    {
        if (s[i] == 'a' || s[i] == 'e') t[i] = 'V';
        else t[i] = 'C';
    }
    
    for (int i = 0; i < s.size() - 1; i++)
    {
        if (t[i] == 'C' && t[i + 1] == 'C')
        {
            pos[i] = 1;
        }
    }
    for (int i = 0; i < s.size(); i++)
    {
        if (i >= s.size() - 2)
        {
            ans += s[i];
            continue;
        }
        if (pos[i])
        {
            ans += s[i];
            ans += '.';
            continue;
        }
        if (t[i] == 'V'&&!pos[i+1])
        {
            ans += s[i];
            ans += '.';
            continue;
        }
        ans += s[i];
    }
    
    cout << ans << "\n";
}

E. Romantic Glasses

Problem - E - Codeforces

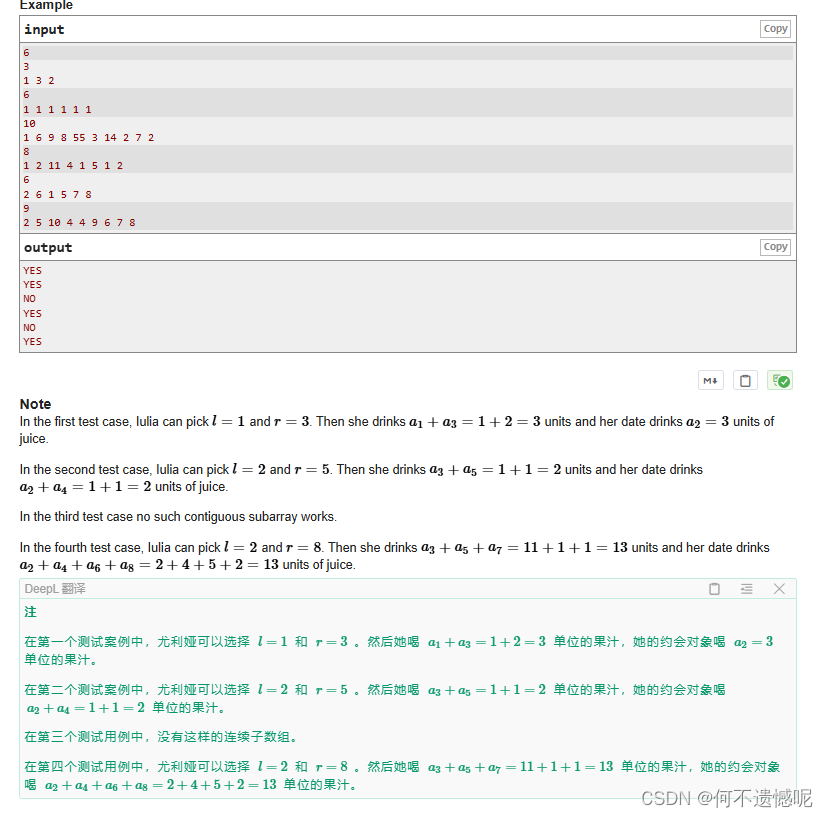
其实就是找到一个连续子数组的奇位与偶位的元素和相同，那我们不妨将所有偶位元素ai设置为-ai，在遍历数组用前缀和记录，当当前前缀和的数字为0或者出现第二次，那么则出现了目标的连续子数组。

ll f[N];
void solve()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> f[i];
    ll sum = 0;
    map<ll,ll>v;
    for (int i = 1; i <= n; i++)
    {
        f[i] *= ((i % 2) ? 1 : -1);
        sum += f[i];
        if (v[sum]||!sum)
        {
            cout << "YES\n";
            return;
        }
        v[sum]++;
    }
    cout << "NO\n";
}

F. Greetings

Problem - F - Codeforces

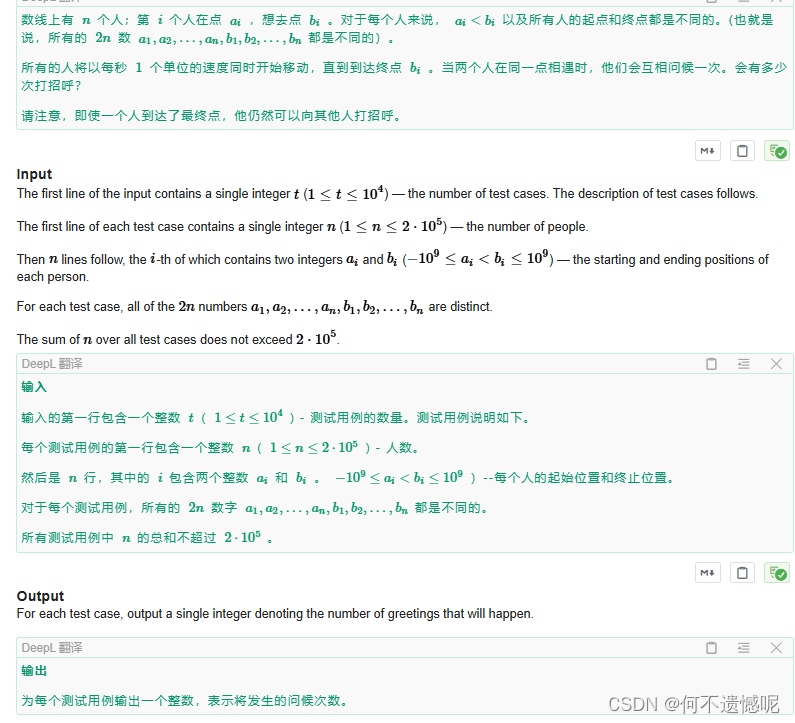
其实就是排序+离散化+树状数组，利用树状数组求逆序对。

当我们对元素按照终点的编号大小按照从小到大排序后，单独将他们的起点编号设置为一个数组，我们发现这个数组的逆序对就是我们要的答案，但是n^2的求解肯定会超时，我们可以用分治或者树状数组去快速求解逆序对，由于本人对树状数组熟悉一些，下面演示的是树状数组求解的代码。

struct Node
{
    ll s,e,id;
}e[N];
ll n;
ll a[N], rak[N];
ll lowbit(ll x)
{
    return x & (-x);
}
bool cmp(Node a, Node b)
{
    return a.e < b.e;
}
bool cmp1(Node a, Node b)
{
    return a.s < b.s;
}
void add(ll pos)
{
    for (int i = pos; i <= n; i += lowbit(i)) a[i] += 1;
}
ll ask(ll pos)
{
    ll ans = 0;
    for (int i = pos; i >= 1; i -= lowbit(i)) ans += a[i];
    return ans;
}
void solve()
{
    memset(a, 0, sizeof(a));
    memset(rak, 0, sizeof(rak));
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> e[i].s >> e[i].e;
    }
    sort(e + 1, e + 1 + n, cmp);
    for (int i = 1; i <= n; i++)
    {
        e[i].id = i;
    }
    sort(e + 1, e + 1 + n,cmp1);
    for (int i = 1; i <= n; i++)
    {
        
        rak[e[i].id] = i;
    }
    ll ans = 0;
    for (int i = 1; i <= n; i++)
    {
        ll pos = rak[i];
        ans += ask(n) - ask(pos);
        add(pos);
    }
    cout << ans << "\n";
}