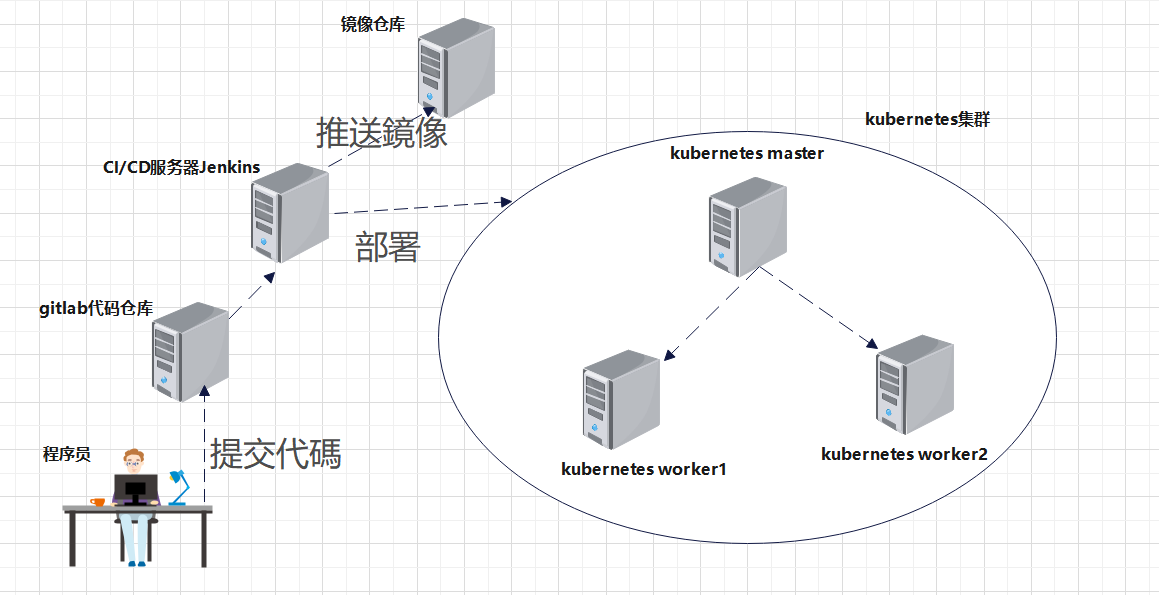
好了,今天我们来了解一下,我们在做练习题中常出现的一个名词。时间复杂度。我相信大家如果有在练习过题目的话。对这个名词应该都不陌生吧。但是可能很少的去思考它是干什么的代表的什么意思。反正我以前练习的时候就是这样。我只知道有这么一个名词在题目里面。但是这个限制的是什么我都不知道。因为在开始的简单练习题中对时间复杂度的要求很低。大家用暴力求解法几乎都可以。但是到后来很多方面都对这个是有要求的了。不再像以前那样,暴力求解都可以解决问题的了。好,我们现在讲这么多。都只是让大家对时间复杂度稍微有一点了解。接下来我们就来详细的介绍一下时间复杂度的含义以及如何计算时间复杂度。
时间复杂度的含义
对于时间复杂度的含义的话我们先用官方的解释来给大家过一遍:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一 个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知 道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个 分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法 的时间复杂度。 这些都是比较官方的书法了我个人觉得这样的解释对于还不太了解时间复杂度的小白来说还是有点太深奥了。要是用我自己理解的白话来讲的话,大家可以想象一下。一个简单的循环。这个循环执行了多少次。然后这个次数就是我们的时间复杂度。我觉得这个解释算是通俗易懂的了。
当然如果所有的时间复杂度都是看一个循环就能得出来的话那就太简单了。我们后面接触的需要考虑时间复杂化度的时候就有很多元素了。在开始的时候大家甚至都可以带一个值进去估算一下。有个大概结果。并且我们的时间复杂度确实不用那么准确。
举例解释时间复杂度
如果我们光讲的话,对时间复杂度的了解肯定是不够的。所以我们还是举一些例子来帮助大家理解。当然是从简单到难得。

大家可以先来看一下这个比较简单的时间复杂度计算题。如果你觉得不能一眼看出来时间复杂度并且还是在前期的时候我们就带值进去计算一下。比如说我们上面我们给的例题,我们先带一个10.然后计算看值是多少?然后再带100,1000分别计算一下。
这里我已经提前计算过来。大家如果感兴趣的话可以自己再去验算一遍。但是啊。大家看。这里我们虽然计算出来了 F(N)的大小,但是大家应该发现了吧。我们平常见到的时间复杂度都是一些什么O()什么什么的吧。是吧。那我们如果照着这样写的话,是不是就很不合大众啊。那么我们也要学习如何用这个大O来表示时间复杂度吧。
大O表示法
对于大O表示法来说咧。我们先来看看正式的解释:是用于描述函数渐进行为的数学符号。出了算法的速度有多快。当然是趋向于操作的次数,因为每种操作的方式不同所需的时间也就无法统一。大O表示法通常作为一个算法优劣的标准,越快越好,数值越小越快。对于官方解释哈。我反正是基本听不懂的。但是有人能听懂啊。所以他们给我讲的时候是这样说的括号里面的取这个公式里面对这个公式影响最大的那个。怎么说咧。例如上面的例子F(N)=N*N+2*N+10。大家可以稍微思考一下这个公式里面对于结果谁的影响是最大的。是不是N*N啊。就是N的平法嘛。因为我不知道怎么打出一模一样的,所以就这样,意思是一样的。好。大家可以理解一下。我们这里是不是n的平方在这个式子里面的影响力最大的。那么我们的大O表示法如何表示咧:O(N*N)。
当然这个式子是固定的但是还有很多式子是无法确定的啊。例如在一个数组里面找一个数这个数一定在数组里面,那么这个式子的时间复杂度如何计算啊。最好情况:1次找到,最坏情况:N次找到,平均情况:N/2次找到。那么这个式子的时间复杂度如何写咧。所以这里我们就引出了大O表示法的另一个规则,我们取最坏的结果。大家都听过一句话,就是要做好最坏的打算。那么这里也是。我们大O表示法也是取最坏的。那么我们这个例子的时间复杂度就为O(N)。
当然有些时候,像上面这个例子直接给我们说了N是多少,比如说m=10,while(m--)。那么我们这里的时间复杂度就是是O(1)了。为什么是O(1)咧。因为我们大O表示法明确表示过。对于N为明确的数值的时候都用1。表示这样表示这个式子的计算速度就是最快的了。因为最坏的情况我们都能一眼看出来,那么这个循环或者递归都应该不是很难了。
当然还有很多的时间复杂度表示方法,这里我就以我们上面讲过的几大排序方法来举例:

我们后面就会很少遇见O(1)的时间复杂化度了。所以,大家可以先看一下大致有哪些时间复杂度的表示方法。
两个循环计算时间复杂度
这里咧我们就不讲单个时间复杂度是如何计算的了。因为如果没有明确的写出循环的个数的话。大多都是O(N)。所以我们这里直接来讲讲双循环是如何计算的。

对与这样简单的分开的两个循环来计算时间复杂度的来说。我们可以分开来看第一个循环是不是关键再与M。然后第二个循环关键在于N。然后我们计算的是++count执行了多少次。那么我们是不是就最好的情况是1+1。两个循环都是一次就结束了。但是最坏的咧。是不是每次都执行完了。那就是M+N了。我们前面也说过取最坏的情况。那么这里我们的时间复杂度是不是就是O(M+N)了。
strchr计算时间复杂度
大家对于strchr的作用应该还没忘吧。就是在一个字符窜里面寻找一个字符。就是我们前面说过的简单的单循环计算。

既然是简单的单循环计算了,那么时间复杂度也是简单的O(N)了吧。
冒泡排序计算时间复杂度
冒泡排序大家肯定都没忘吧。毕竟大家还是小白的时候应该都写过这个吧。接下来我们就是来尝试计算一下冒泡排序的时间复杂度。
我们来看看冒泡排序最好的情况就是执行n次就结束了。但是最坏的情况就是内部不是有序数列,那么就 当end=n-1的时候内部就要执行n-2次。当end=n-2的时候内部就要执行n-3次....当end=2时,内部就执行1次end=1时内部执行0次。end不能为0。那么这个循环是不是就是(1+n-1)*n/2然后我们整合一下就是(n*2)/2。那么最坏的情况下,影响最大的就是n*2了。那么冒泡排序的大O表示法就是O(n*2)。大家应该明白吧。就是稍微带值进去计算得出个大概规律。我们不需要十分准确,有个大概就是可以了。如果太精确也没啥意义其实。
递归计算时间复杂度
讲了上面几个例子接下里我们讲讲另外一个常见的计算时间复杂度的。递归。这个也是我们前期学过的了。那么递归的时间复杂度如何计算咧。
这个递归是很简单的。我们只需要康康n就可以了。也可能一次就结束了,也有可能要n次。那么老规矩取最坏的情况。我们就取n。所以这个递归的时间复杂度为O(N)。
递归斐波拉契数计算时间复杂度
递归斐波拉契数的这个难度可就不是上面的那些简单就能想出来的了哦。我们建议计算这个最好是画一画图递归栈帧的二叉树讲解。反正已经学过二叉树了。我们就用起来然后帮助理解。

斐波那契数列是这样一个数列:1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765…
表达式为: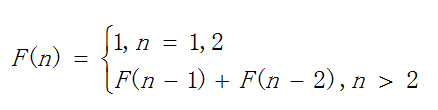

对于Fib(5)的递归过程可知,执行次数最多不超过但接近于二叉树最多时候的节点数,可近似看为2 n − 1 2^n-12 n −1,所以时间复杂度T(n)为2 n 2^n2 n的同阶,即T ( n ) = O ( 2 n ) T(n)=O(2^n)T(n)=O(2 n )在递归调用的过程中,除了存放程序本身所用的指令和变量,还需要另外开辟n个变量来作为辅助空间,分别对应Fib(n-1),Fib(n-2),Fib(n-3),…,Fib(0)中的n-1,n-2,n-3,…,0。因此,空间复杂度为O (n)。
总结
好了,当大家看到这里我想应该就对计算时间复杂度有一些了解了吧。反正我一直用的都是带几个值进去计算一下。然后就可以得出一个大概的逻辑这样得出一个大概的就可以了。那么今天的时间复杂度计算就到这里了。下一篇我们会分享一下空间复杂度的计算。