第十三章第十八题(使用 Rational 类)

题目要求：

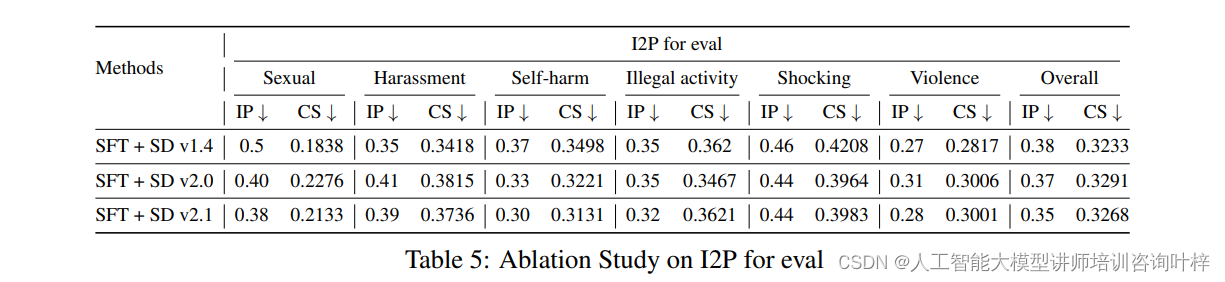
• 编写程序，使用 Rational 类计算下面的求和数列:

• 你将会发现输出是不正确的 ，因为整数溢出(太大了)。为了解决这个问题 ，参见编程练习題13.15。
• 代码参考：

package chapter_13;

import java.math.BigInteger;

public class 编程练习题13_18RationalSum {
    public static void main(String[] args) {
        Rational2 resultRational2 = new Rational2();
        for (long i = 2; i <= 100; i++) {
            Rational2 rational2 = new Rational2(BigInteger.valueOf(i-1), BigInteger.valueOf(i));
            System.out.print(rational2.toString());

            if (i == 100) System.out.print(" = ");
            else if (i % 10 == 0) System.out.println(" + ");
            else System.out.print(" + ");

            resultRational2 = resultRational2.add(rational2);
        }
        //System.out.println(resultRational2);
        System.out.println(resultRational2.simplify());
    }
}

class Rational2 extends Number implements Comparable<Rational2> {
    private BigInteger numerator = BigInteger.ZERO;
    private BigInteger denominator = BigInteger.ONE;

    public Rational2() {
        this(BigInteger.ZERO, BigInteger.ONE);
    }

    public Rational2(BigInteger numerator, BigInteger denominator) {
        BigInteger gcd = numerator.gcd(denominator);
        this.numerator = numerator.divide(gcd);
        this.denominator = denominator.divide(gcd);
        if (this.denominator.compareTo(BigInteger.ZERO) < 0) { // 确保分母为正
            this.numerator = this.numerator.negate();
            this.denominator = this.denominator.negate();
        }
    }

    private static BigInteger gcd(BigInteger n, BigInteger d) {
        return n.gcd(d);
    }

    public BigInteger getNumerator() {
        return numerator;
    }

    public BigInteger getDenominator() {
        return denominator;
    }

    public Rational2 add(Rational2 secondRational) {
        BigInteger n = numerator.multiply(secondRational.getDenominator())
                                .add(denominator.multiply(secondRational.getNumerator()));
        BigInteger d = denominator.multiply(secondRational.getDenominator());
        return new Rational2(n, d);
    }

    public Rational2 subtract(Rational2 secondRational) {
        BigInteger n = numerator.multiply(secondRational.getDenominator())
                                .subtract(denominator.multiply(secondRational.getNumerator()));
        BigInteger d = denominator.multiply(secondRational.getDenominator());
        return new Rational2(n, d);
    }

    public Rational2 multiply(Rational2 secondRational) {
        BigInteger n = numerator.multiply(secondRational.getNumerator());
        BigInteger d = denominator.multiply(secondRational.getDenominator());
        return new Rational2(n, d);
    }

    public Rational2 divide(Rational2 secondRational) {
        if (secondRational.getNumerator().equals(BigInteger.ZERO)) {
            throw new ArithmeticException("Division by zero");
        }
        BigInteger n = numerator.multiply(secondRational.getDenominator());
        BigInteger d = denominator.multiply(secondRational.getNumerator());
        return new Rational2(n, d);
    }

    @Override
    public String toString() {
        return denominator.equals(BigInteger.ONE) ? numerator.toString() : numerator + "/" + denominator;
    }

    @Override
    public boolean equals(Object other) {
        if (other instanceof Rational2) {
            Rational2 that = (Rational2) other;
            return this.subtract(that).getNumerator().equals(BigInteger.ZERO);
        }
        return false;
    }

    @Override
    public int intValue() {
        return numerator.intValue() / denominator.intValue(); // 注意：这可能会损失精度
    }

    @Override
    public float floatValue() {
        return (float)doubleValue();
    }

    @Override
    public double doubleValue() {
        return numerator.doubleValue() / denominator.doubleValue();
    }

    @Override
    public long longValue() {
        return numerator.longValue() / denominator.longValue(); // 同样注意精度损失
    }

    @Override
    public int compareTo(Rational2 o) {
        return this.subtract(o).getNumerator().signum();
    }
    public Rational2 simplify() {
        BigInteger gcd = numerator.gcd(denominator);
        return new Rational2(numerator.divide(gcd), denominator.divide(gcd));
    }
}

• 输出结果：
   

1/2 + 2/3 + 3/4 + 4/5 + 5/6 + 6/7 + 7/8 + 8/9 + 9/10 + 
10/11 + 11/12 + 12/13 + 13/14 + 14/15 + 15/16 + 16/17 + 17/18 + 18/19 + 19/20 + 
20/21 + 21/22 + 22/23 + 23/24 + 24/25 + 25/26 + 26/27 + 27/28 + 28/29 + 29/30 + 
30/31 + 31/32 + 32/33 + 33/34 + 34/35 + 35/36 + 36/37 + 37/38 + 38/39 + 39/40 + 
40/41 + 41/42 + 42/43 + 43/44 + 44/45 + 45/46 + 46/47 + 47/48 + 48/49 + 49/50 + 
50/51 + 51/52 + 52/53 + 53/54 + 54/55 + 55/56 + 56/57 + 57/58 + 58/59 + 59/60 + 
60/61 + 61/62 + 62/63 + 63/64 + 64/65 + 65/66 + 66/67 + 67/68 + 68/69 + 69/70 + 
70/71 + 71/72 + 72/73 + 73/74 + 74/75 + 75/76 + 76/77 + 77/78 + 78/79 + 79/80 + 
80/81 + 81/82 + 82/83 + 83/84 + 84/85 + 85/86 + 86/87 + 87/88 + 88/89 + 89/90 + 
90/91 + 91/92 + 92/93 + 93/94 + 94/95 + 95/96 + 96/97 + 97/98 + 98/99 + 99/100 = 264414864639329557497913717698145082779489/2788815009188499086581352357412492142272