MXNet实现图片的样式风格迁移(Style Transfer)

样式迁移就是将一个样式（风格）应用到一张主图上，改变这张图片的风格，比如说拍摄了一张夜晚的图片，我们可以拿梵高的"星月夜"图片做样式，应用到拍摄的图片上，两者合成后的新图片，风格就有了梵高的风格了

原理与操作都比较简单，准备两张图片，一张做内容，一张做样式，然后分别对它们进行特征的抽取，内容图片抽取内容特征，样式图片就抽取样式特征，进行合成。

其中抽取特征一般使用卷积神经网络，本节我们使用VGG-19预训练模型。

在模型中抽取不同层，分别抽取内容特征与样式特征，其中抽取内容特征，需靠近输出层，本节我们是抽取第25层(实质第26层)，因为如果靠近输入层抽取特征的话，抽取的是一些细节，一些纹理之类，而这些细节我们就当成风格来抽取吧。抽取细节，本节共抽取5层，分别是第0层，5层，10层，19层，28层的特征作为样式特征。

上面是整个流程的大概介绍，下面我们来具体的实现它。

图片的标准化处理

首先就是对输入图像的处理，需要做一些标准化处理，以及形状的变换，让其适合这个模型的训练：

import d2lzh as d2l
from mxnet import autograd, gluon, image, init, nd
from mxnet.gluon import model_zoo, nn
import time
# 读取内容图像和样式图像
d2l.set_figsize()
c_img = image.imread('content.jpg')
# print(c_img.shape)#(501, 800, 3)高、宽、通道(H,W,C)
# d2l.plt.imshow(c_img.asnumpy())#mxnet.ndarray.ndarray.NDArray转numpy.ndarray

s_img = image.imread('style.jpg')
# print(s_img.shape)#(334, 800, 3)
# d2l.plt.imshow(s_img.asnumpy())
# 预处理函数和后处理函数
rgb_mean = nd.array([0.485, 0.456, 0.406])
rgb_std = nd.array([0.229, 0.224, 0.225])


def preprocess(img, img_shape):
    '''将图像做标准化处理(N,C,H,W)'''
    img = image.imresize(img, *img_shape)
    img = (img.astype('float32')/255 - rgb_mean) / rgb_std
    return img.transpose((2, 0, 1)).expand_dims(axis=0)

def postprocess(img):
    '''
    图像打印函数要求每个像素的浮点数值在0到1之间
    我们使用clip函数对小于0和大于1的值分别取0和1
    (H,W,C)
    '''
    img = img[0].as_in_context(rgb_std.context)
    return (img.transpose((1, 2, 0))*rgb_std+rgb_mean).clip(0, 1)

图像的处理比较简单，需要注意的是，读取出来的形状是高、宽、通道(H,W,C),如果显示的话，需要asnumpy())转换成numpy.ndarray类型。在神经网络中的适配形状(N,C,H,W)，所以增加一个批处理维度之后，再transpose转置形状即可

VGG-19网络模型

然后通过预处理模型VGG-19来构建新的网络模型，在model_zoo模块中有很多可选的预处理的模型：pretrained_net=model_zoo.vision.vgg19(pretrained=True)

VGG-19模型参数文件vgg19-ad2f660d.params，压缩包507M，如果直接下载的时候比较慢，可以使用迅雷直接下载。

下载解压到这个目录即可：

Downloading C:\Users\Tony\AppData\Roaming\mxnet\models\vgg19-ad2f660d.zip from https://apache-mxnet.s3-accelerate.dualstack.amazonaws.com/gluon/models/vgg19-ad2f660d.zip

当然如果不需要预训练的话，也就是不需要参数文件，只加载网络模型的结构，可以让参数pretrained=False，这样就不会下载参数文件了。

我们打印VGG-19的网络的整个架构看下，可以看到是一个深度卷积神经网络：

VGG(
(features): HybridSequential(
(0): Conv2D(3 -> 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): Activation(relu)
(2): Conv2D(64 -> 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): Activation(relu)
(4): MaxPool2D(size=(2, 2), stride=(2, 2), padding=(0, 0), ceil_mode=False, global_pool=False, pool_type=max, layout=NCHW)
(5): Conv2D(64 -> 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): Activation(relu)
(7): Conv2D(128 -> 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): Activation(relu)
(9): MaxPool2D(size=(2, 2), stride=(2, 2), padding=(0, 0), ceil_mode=False, global_pool=False, pool_type=max, layout=NCHW)
(10): Conv2D(128 -> 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): Activation(relu)
(12): Conv2D(256 -> 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): Activation(relu)
(14): Conv2D(256 -> 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): Activation(relu)
(16): Conv2D(256 -> 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(17): Activation(relu)
(18): MaxPool2D(size=(2, 2), stride=(2, 2), padding=(0, 0), ceil_mode=False, global_pool=False, pool_type=max, layout=NCHW)
(19): Conv2D(256 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): Activation(relu)
(21): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): Activation(relu)
(23): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(24): Activation(relu)
(25): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(26): Activation(relu)
(27): MaxPool2D(size=(2, 2), stride=(2, 2), padding=(0, 0), ceil_mode=False, global_pool=False, pool_type=max, layout=NCHW)
(28): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): Activation(relu)
(30): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(31): Activation(relu)
(32): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(33): Activation(relu)
(34): Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(35): Activation(relu)
(36): MaxPool2D(size=(2, 2), stride=(2, 2), padding=(0, 0), ceil_mode=False, global_pool=False, pool_type=max, layout=NCHW)
(37): Dense(25088 -> 4096, Activation(relu))
(38): Dropout(p = 0.5, axes=())
(39): Dense(4096 -> 4096, Activation(relu))
(40): Dropout(p = 0.5, axes=())
)
(output): Dense(4096 -> 1000, linear)
)

前面介绍说了，为了避免合成的图像过多的保留内容图像的细节，我们从VGG中选择靠近输出的层，来抽取内容特征，我们叫做内容层；从VGG中选择不同层的输出来匹配全局和全局的样式，这些层我们叫做样式层。

比如我们想要获取25层的特征值(这里我们选用为内容层)，可以这样获取：

pretrained_net.features[25]

是一个卷积核是3x3，步幅为1，填充为1的二维卷积层

Conv2D(512 -> 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))

新建网络

接下来我们新建一个网络，抽取VGG里面的层来分别保存内容特征和样式特征。

pretrained_net=model_zoo.vision.vgg19(pretrained=True)
#选取内容层与样式层
content_layers,style_layers=[25],[0,5,10,19,28]
#构建一个新网络(29层)
net=nn.Sequential()
for i in range(max(content_layers+style_layers)+1):
    net.add(pretrained_net.features[i])

#net(X)的输出只有一个输出，而这里需要两个(内容与样式)
def extract_features(X,content_layers,style_layers):
    '''分别保存内容层与样式层的输出'''
    contents=[]
    styles=[]
    for i in range(len(net)):
        X=net[i](X)
        if i in content_layers:
            contents.append(X)
        if i in style_layers:
            styles.append(X)
    return contents,styles

#抽取内容图像的内容特征
def get_contents(img_shape,ctx):
    content_X=preprocess(c_img,img_shape).copyto(ctx)
    contents_Y,_=extract_features(content_X,content_layers,style_layers)
    return content_X,contents_Y

#抽取样式图像的样式特征
def get_styles(img_shape,ctx):
    style_X=preprocess(s_img,img_shape).copyto(ctx)
    _,styles_Y=extract_features(style_X,content_layers,style_layers)
    return style_X,styles_Y

这里使用vgg19网络模型，然后通过这个模型分别抽取内容和样式，内容是整体，是主题，所以不考虑细节，而样式就是细节，纹理等，所以抽取多个靠近输入层的输出来做样式特征。

损失函数

新模型构建好了之后，就开始定义损失函数，这里有三个损失函数：

内容损失：通过平方误差函数衡量合成图像与内容图像在内容特征上的差异，使得合成图像在内容特征上接近内容图像

def content_loss(Y_hat, Y):
    '''内容损失'''
    return (Y_hat-Y).square().mean()

样式损失：通过平方误差函数衡量合成图像与样式图像在样式上的差异，使得合成图像在样式特征上接近样式图像

def gram(X):
    """格拉姆矩阵"""
    num_channels, n = X.shape[1], X.size//X.shape[1]
    X = X.reshape((num_channels, n))
    return nd.dot(X, X.T)/(num_channels*n)
def style_loss(Y_hat, gram_Y):
    '''样式损失'''
    return ((gram(Y_hat)-gram_Y).square().mean())

总变差损失：主要是对合成图像里面大量高频噪点做降噪处理，常用的就是总变差降噪（total variation denoising），这样的处理有助于减少合成图像中的噪点。

def tv_loss(Y_hat):
    '''总变差损失'''
    return 0.5*((Y_hat[:, :, 1:, :]-Y_hat[:, :, :-1, :]).abs().mean()+
                (Y_hat[:, :, :, 1:]-Y_hat[:,:,:,:-1]).abs().mean())

损失函数就是三者损失函数的加权和，我们可以调节它们三者的权重值，来权衡合成图像在保留内容、迁移样式以及降噪三方面的相对重要性。

content_w, style_w, tv_w = 1, 1e3, 50
def compute_loss(X, contents_Y_hat, styles_Y_hat, contents_Y, styles_Y_gram):
    contents_l = [content_loss(Y_hat, Y)*content_w for Y_hat,Y in zip(contents_Y_hat, contents_Y)]
    styles_l = [style_loss(Y_hat, Y)*style_w for Y_hat,Y in zip(styles_Y_hat, styles_Y_gram)]
    tv_l = tv_loss(X)*tv_w
    # 所有损失求和
    l = nd.add_n(*styles_l)+nd.add_n(*contents_l)+tv_l
    return contents_l, styles_l, tv_l, l

让风格凸显点，就调大style_w样式权重值，三者权重值有兴趣的可以试着改变看看效果

训练模型

最后一步就做训练，在这个样式迁移中，合成图像是唯一需要更新的变量。

假如 $\text{[math]}$ 表示坐标(i,j)的像素值，其降低总变差损失的公式如下：

$\text{[math]}$

尽可能使得邻近的像素值相似。

在训练的时候，不断的抽取合成图像的内容特征和样式特征，并计算损失函数。由于每隔50个迭代周期才调用同步函数asscalar，很容易造成内存占用过高，因此我们在每个迭代周期都调用一次同步函数waitall

这里我使用的样式图片是目前很热门的《中国奇谭》中的《鹅鹅鹅》图片，很喜欢的水墨画风格，我们来看下合成之后的效果会是什么样的。

全部代码如下：

import d2lzh as d2l
from mxnet import autograd, gluon, image, init, nd
from mxnet.gluon import model_zoo, nn
import time

# 读取内容图像和样式图像
d2l.set_figsize()
c_img = image.imread('content.jpg')
# print(c_img.shape)#(501, 800, 3)高、宽、通道(H,W,C)
# d2l.plt.imshow(c_img.asnumpy())#mxnet.ndarray.ndarray.NDArray转numpy.ndarray

s_img = image.imread('style.jpg')
# print(s_img.shape)#(334, 800, 3)
# d2l.plt.imshow(s_img.asnumpy())

# 预处理函数和后处理函数
rgb_mean = nd.array([0.485, 0.456, 0.406])
rgb_std = nd.array([0.229, 0.224, 0.225])


def preprocess(img, img_shape):
    '''将图像做标准化处理(N,C,H,W)'''
    img = image.imresize(img, *img_shape)
    img = (img.astype('float32')/255 - rgb_mean) / rgb_std
    return img.transpose((2, 0, 1)).expand_dims(axis=0)

def postprocess(img):
    '''
    图像打印函数要求每个像素的浮点数值在0到1之间
    我们使用clip函数对小于0和大于1的值分别取0和1
    (H,W,C)
    '''
    img = img[0].as_in_context(rgb_std.context)
    return (img.transpose((1, 2, 0))*rgb_std+rgb_mean).clip(0, 1)


"""通过VGG-19模型构建新的网络"""
# 预训练模型VGG-19
pretrained_net = model_zoo.vision.vgg19(pretrained=True)
# print(pretrained_net)
# 抽取内容层与样式层
content_layers, style_layers = [25], [0, 5, 10, 19, 28]
# 构建一个新网络(29层)
net = nn.Sequential()
for i in range(max(content_layers+style_layers)+1):
    net.add(pretrained_net.features[i])

# 由于net(X)的输出只有一个输出，而这里需要两个(内容与样式)
def extract_features(X, content_layers, style_layers):
    '''分别抽取并保存内容层与样式层的输出'''
    contents = []
    styles = []
    for i in range(len(net)):
        X = net[i](X)
        if i in content_layers:
            contents.append(X)
        if i in style_layers:
            styles.append(X)
    return contents, styles

# 抽取内容图像的内容特征
def get_contents(img_shape, ctx):
    content_X = preprocess(c_img, img_shape).copyto(ctx)
    contents_Y, _ = extract_features(content_X, content_layers, style_layers)
    return content_X, contents_Y

# 抽取样式图像的样式特征
def get_styles(img_shape, ctx):
    style_X = preprocess(s_img, img_shape).copyto(ctx)
    _, styles_Y = extract_features(style_X, content_layers, style_layers)
    return style_X, styles_Y


"""定义损失函数"""
def content_loss(Y_hat, Y):
    '''内容损失'''
    return (Y_hat-Y).square().mean()

def gram(X):
    """格拉姆矩阵"""
    num_channels, n = X.shape[1], X.size//X.shape[1]
    X = X.reshape((num_channels, n))
    return nd.dot(X, X.T)/(num_channels*n)
def style_loss(Y_hat, gram_Y):
    '''样式损失'''
    return ((gram(Y_hat)-gram_Y).square().mean())

def tv_loss(Y_hat):
    '''总变差损失'''
    return 0.5*((Y_hat[:, :, 1:, :]-Y_hat[:, :, :-1, :]).abs().mean()+
                (Y_hat[:, :, :, 1:]-Y_hat[:,:,:,:-1]).abs().mean())


# 损失函数：上面三者损失的加权和
content_w, style_w, tv_w = 1, 1e3, 50
def compute_loss(X, contents_Y_hat, styles_Y_hat, contents_Y, styles_Y_gram):
    contents_l = [content_loss(Y_hat, Y)*content_w for Y_hat,Y in zip(contents_Y_hat, contents_Y)]
    styles_l = [style_loss(Y_hat, Y)*style_w for Y_hat,Y in zip(styles_Y_hat, styles_Y_gram)]
    tv_l = tv_loss(X)*tv_w
    # 所有损失求和
    l = nd.add_n(*styles_l)+nd.add_n(*contents_l)+tv_l
    return contents_l, styles_l, tv_l, l


"""合成图像"""
# 在样式迁移中，合成图像是唯一需要更新的变量
class GeneratedImage(nn.Block):
    """将合成图像视为模型参数"""
    def __init__(self, img_shape, **kwargs):
        super(GeneratedImage, self).__init__(**kwargs)
        self.weight = self.params.get('weight', shape=img_shape)

    def forward(self):
        return self.weight.data()

# 创建合成图像的模型实例，并将其初始化为图像X
# 样式图像在各个样式层的格拉姆矩阵styles_Y_gram将在训练前预先计算好
def get_inits(X, ctx, lr, styles_Y):
    gen_img = GeneratedImage(X.shape)
    gen_img.initialize(init.Constant(X), ctx=ctx, force_reinit=True)
    trainer = gluon.Trainer(gen_img.collect_params(),'adam', {'learning_rate': lr})
    styles_Y_gram = [gram(Y) for Y in styles_Y]
    return gen_img(), styles_Y_gram, trainer


"""训练模型"""
def train(X, contents_Y, styles_Y, ctx, lr, max_epochs, lr_decay_epoch):
    X, styles_Y_gram, trainer = get_inits(X, ctx, lr, styles_Y)
    for i in range(max_epochs):
        start = time.time()
        with autograd.record():
            contents_Y_hat, styles_Y_hat = extract_features(X, content_layers, style_layers)
            contents_l, styles_l, tv_l, l = compute_loss(X, contents_Y_hat, styles_Y_hat, contents_Y, styles_Y_gram)
        l.backward()
        trainer.step(1)
        nd.waitall()
        if i % 50 == 0 and i != 0:
            print('epoch %3d,内容损失 %.2f,样式损失 %.2f,总变差损失 %.2f, %.2f秒' % (i, nd.add_n(*contents_l).asscalar(),
                                                                       nd.add_n(*styles_l).asscalar(), tv_l.asscalar(), time.time()-start))
        if i % lr_decay_epoch == 0 and i != 0:
            trainer.set_learning_rate(trainer.learning_rate*0.1)
            print('衰减后的学习率：%.1e' % trainer.learning_rate)
    return X

# 图片宽,高(W,H)
ctx, img_shape = d2l.try_gpu(), (200, 100)
net.collect_params().reset_ctx(ctx)
content_X, contents_Y = get_contents(img_shape, ctx)
_, styles_Y = get_styles(img_shape, ctx)
output = train(content_X, contents_Y, styles_Y, ctx, 0.01, 500, 200)
d2l.plt.imsave('new-style.jpg',postprocess(output).asnumpy())

#尺寸调大
ctx,image_shape=d2l.try_gpu(), (560,320)
_,content_Y=get_contents(image_shape,ctx)
_,style_Y=get_styles(image_shape,ctx)
X=preprocess(postprocess(output)*255,image_shape)
output=train(X,content_Y,style_Y,ctx,0.01,300,100)
d2l.plt.imsave('big-new-style.jpg',postprocess(output).asnumpy())

epoch 50,内容损失 59.70,样式损失 77.01,总变差损失 14.96, 0.04秒
epoch 100,内容损失 55.44,样式损失 51.54,总变差损失 15.23, 0.04秒
epoch 150,内容损失 53.06,样式损失 41.99,总变差损失 15.33, 0.04秒
epoch 200,内容损失 51.30,样式损失 37.01,总变差损失 15.34, 0.04秒
衰减后的学习率：1.0e-03
epoch 250,内容损失 51.09,样式损失 36.52,总变差损失 15.32, 0.04秒
epoch 300,内容损失 50.92,样式损失 36.09,总变差损失 15.31, 0.04秒
epoch 350,内容损失 50.76,样式损失 35.66,总变差损失 15.30, 0.04秒
epoch 400,内容损失 50.61,样式损失 35.23,总变差损失 15.28, 0.05秒
衰减后的学习率：1.0e-04
epoch 450,内容损失 50.59,样式损失 35.19,总变差损失 15.28, 0.04秒
epoch 50,内容损失 9.28,样式损失 8.89,总变差损失 5.67, 0.28秒
epoch 100,内容损失 7.61,样式损失 7.23,总变差损失 5.09, 0.27秒
衰减后的学习率：1.0e-03
epoch 150,内容损失 7.51,样式损失 7.10,总变差损失 5.00, 0.27秒
epoch 200,内容损失 7.43,样式损失 7.01,总变差损失 4.94, 0.26秒
衰减后的学习率：1.0e-04
epoch 250,内容损失 7.42,样式损失 7.00,总变差损失 4.93, 0.27秒

保存的尺寸比较小，尝试调大点，当然这个取决于你的内存与显存的大小，我的配置比较低，已尽量调大到不让内存溢出的情况：

ctx,image_shape=d2l.try_gpu(), (560,320)
_,content_Y=get_contents(image_shape,ctx)
_,style_Y=get_styles(image_shape,ctx)
X=preprocess(postprocess(output)*255,image_shape)
output=train(X,content_Y,style_Y,ctx,0.01,300,100)
d2l.plt.imsave('big-new-style.jpg',postprocess(output).asnumpy())

两张原图如下，一张内容图，一张样式图：

然后贴出大的合成图片，可以看出，内容大体是没有多大变化，整张图片的风格带了点“鹅鹅鹅”的味道！

当然这些合成的图片，一般来说原图与样式图尽量保持一样，差异只在于风格上，这样出来的效果会更好，这里只是一个示例，有兴趣的伙伴可以多合成一些看看。

格拉姆矩阵(Gram matrix)

在样式损失函数，我们发现出现一个新的知识点：格拉姆矩阵

先来看下它的定义，n维欧式空间中任意k个向量之间两两的内积(dot)所组成的矩阵，称为这k个向量的格拉姆矩阵(Gram matrix)，很明显，这是一个对称矩阵，回到前面的格拉姆函数

def gram(X):
    """格拉姆矩阵"""
    num_channels, n = X.shape[1], X.size//X.shape[1]
    X = X.reshape((num_channels, n))
    return nd.dot(X, X.T)/(num_channels*n)

这里也可以看到，返回的是(通道数,通道数)这样的形状，是对称的。

在这节的例子中，输入图像特征的形状是(N,C,H,W)。我们经过flatten(将H*W进行平铺成一维向量)和矩阵转置操作，可以变形为(C,N*H*W)和(N*H*W, C)的矩阵，然后内积就得到格拉姆矩阵，得到的形状是(C,C)，换句话说，在特征图上每个像素值都来自一个特定卷积核在特定位置的卷积，因此每个像素值表示一个特征的强度，而格拉姆矩阵计算的是两两特征之间的相关性。

题外话：这里既然是特定位置的卷积，也反映着特征之间的相关性，那感觉跟互相关的概念很像了，互相关的定义是两个函数分别做复数共轭和反向平移并使其相乘的无穷积分。当然个人的通俗理解其实很简单，就是加权和的意思，使用一小段代码来验证下，相乘以及互相关，而互相关的结果就是相乘之后的和：

import d2lzh as d2l

a=nd.array([[1,2],[3,4]])
b=nd.array([[1,2],[6,7]])
>>> a*b

[[ 1.  4.]
 [18. 28.]]
<NDArray 2x2 @cpu(0)>

>>> d2l.corr2d(a,b)

[[51.]]
<NDArray 1x1 @cpu(0)>

格拉姆矩阵的每个值可以说是代表i通道的特征图j通道的特征图的互相关程度。

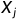假设样本数N=1的情况，这里的X可以看作有C个长度为H*W的向量 $\text{[math]}$ 组成，其中向量 $\text{[math]}$ 代表了通道i上的样式特征，这些向量的格拉姆矩阵(向量 $\text{[math]}$ 与 $\text{[math]}$ 的内积)，就表达了通道i和通道j上样式特征的相关性。

当然函数除以了(num_channels*n)这个是为了避免H*W出现较大的值，为了让样式损失不受这些值的大小的影响的一个做法。

可能初次接触格拉姆矩阵的伙伴们会有点不很明白，如果说熟悉协方差的话，那理解起来就更简单了，我们再看下它的样式损失：

def style_loss(Y_hat, gram_Y):
    '''样式损失'''
    return ((gram(Y_hat)-gram_Y).square().mean())

那么对这种格拉姆矩阵的差异，换种理解方式就是体现两者之间的方向，如果说大于0，说明总体来说是方向相同的，值越大说明越相似，反之小于0说明方向相反，它们之间的差异越大，这样应该明白了我们就是尽量让样式接近，方向肯定一样，这样就效果越好。

当然限于水平问题，不够严谨，只能说尽量帮助大家理解，对这些理解可能也不是很准，望留言指正！

最后附加一张内容抽取与样式抽取的损失函数的结构图

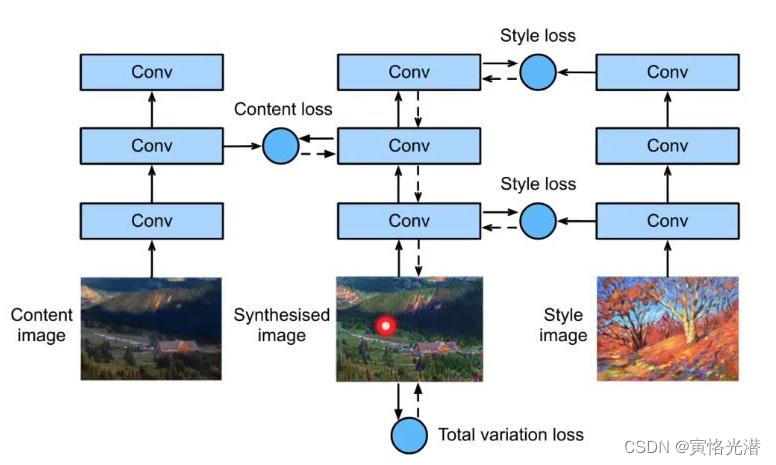
实线箭头是样式迁移的损失函数，虚线箭头是迭代模型参数，就是不断的更新合成的图像！