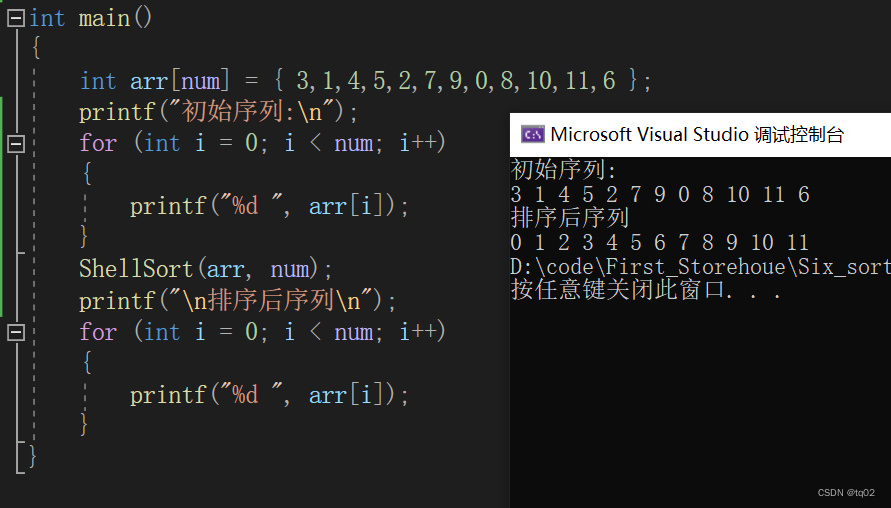
与软件开发相比，人工智能领域需要大量数学知识。主要涉及微积分、线性代数、概率论和最优化。

本文主要介绍人工智能里用到了哪些数学知识，试图向您提供一个目录式的、导读式的概述。后期计划一一展开讲解。

本文作为我学习人工智能的笔记，主要供自己以后温故知新，在此梳理一遍也算是二次学习。如对您有所帮助，不甚荣幸。若所言有误，十分欢迎指正。如有侵权，请联系作者删除。

---

1. • 微积分

在机器学习中，主要用到了微积分中的微分部分，其作用是求函数的极值，就是很多机器学习库中的求解器（solver）所实现的功能。

在机器学习中主要涉及到的微积分知识点：

• 导数和偏导数的定义与计算方法

• 梯度向量的定义

• 极值定理，可导函数在极值点处导数或梯度必须为 0

• 雅克比矩阵，这是向量到向量映射函数的偏导数构成的矩阵，在求导推导中会用到

• Hessian 矩阵，这是 2 阶导数对多元函数的推广，与函数的极值有密切的联系

• 凸函数的定义与判断方法

• 泰勒展开公式

• 拉格朗日乘数法，用于求解带等式约束的极值问题

其中最核心的是多元函数的泰勒展开公式，据此我们可以推导出机器学习中常用的梯度下降法，牛顿法，拟牛顿法等一系列最优化方法。

泰勒公式：

2. • 线性代数

微积分和线性代数，微积分中会用到大量线性代数的知识，线性代数中也会用到微积分的知识。相比之下，线性代数用的更多。

在机器学习的几乎所有地方都有使用，具体用到的知识点有：

• 向量和它的各种运算，包括加法，减法，数乘，转置，内积

• 向量和矩阵的范数，L1 范数和 L2 范数

• 矩阵和它的各种运算，包括加法，减法，乘法，数乘

• 逆矩阵的定义与性质

• 行列式的定义与计算方法

• 二次型的定义

• 矩阵的正定性

• 矩阵的特征值与特征向量

• 矩阵的奇异值分解SVD

• 线性方程组的数值解法，尤其是共轭梯度法

机器学习算法处理的数据一般都是向量、矩阵或者张量。经典的机器学习算法输入的数据都是特征向量，深度学习算法在处理图像时输入的是 2 维的矩阵或者 3 维的张量。

3. • 概率论

如果把机器学习所处理的样本数据看作随机变量/向量，我们就可以用概率论的观点对问题进行建模，这代表了机器学习中很大一类方法。

在机器学习里用到的概率论知识点有:

• 随机事件的概念，概率的定义与计算方法

• 随机变量与概率分布，尤其是连续型随机变量的概率密度函数和分布函数

• 条件概率与贝叶斯公式

• 常用的概率分布，包括正态分布，伯努利二项分布，均匀分布

• 随机变量的均值与方差，协方差

• 随机变量的独立性

• 最大似然估计

4. • 最优化

几乎所有机器学习算法归根到底都是在求解最优化问题。求解最优化问题的指导思想是在极值点处函数的导数/梯度必须为 0。因此你必须理解梯度下降法、牛顿法这两种常用的算法，它们的迭代公式都可以从泰勒展开公式中得到。如果能知道坐标下降法、拟牛顿法就更好了。

凸优化是机器学习中经常会提及的一个概念，这是一类特殊的优化问题，它的优化变量的可行域是凸集，目标函数是凸函数。凸优化最好的性质是它的所有局部最优解就是全局最优解，因此求解时不会陷入局部最优解。如果一个问题被证明为是凸

优化问题，基本上已经宣告此问题得到了解决。在机器学习中，线性回归、岭回归、支持向量机、logistic 回归等很多算法求解的都是凸优化问题。

拉格朗日对偶为带等式和不等式约束条件的优化问题构造拉格朗日函数，将其变为原问题，这两个问题是等价的。通过这一步变换，将带约束条件的问题转换成不带约束条件的问题。通过变换原始优化变量和拉格朗日乘子的优化次序，进一步将原问题转换为对偶问题，如果满足某种条件，原问题和对偶问题是等价的。这种方法的意义在于可以将一个不易于求解的问题转换成更容易求解的问题。在支持向量机中有拉格朗日对偶的应用。

KKT 条件是拉格朗日乘数法对带不等式约束问题的推广，它给出了带等式和不等式约束的优化问题在极值点处所必须满足的条件。在支持向量机中也有它的应用。

如果你没有学过最优化方法这门课也不用担心，这些方法根据微积分和线性代数的基础知识可以很容易推导出来。如果需要系统的学习这方面的知识，可以阅读《凸优化》，《非线性规划》两本经典教材。

5. • 总结

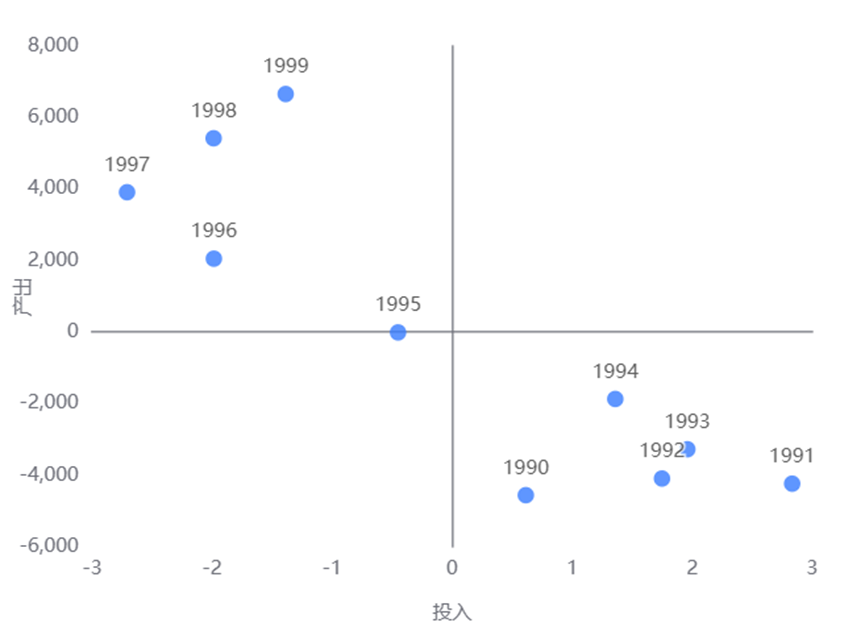
这里整理了人工智能相关算法所涉及到的数学知识点：

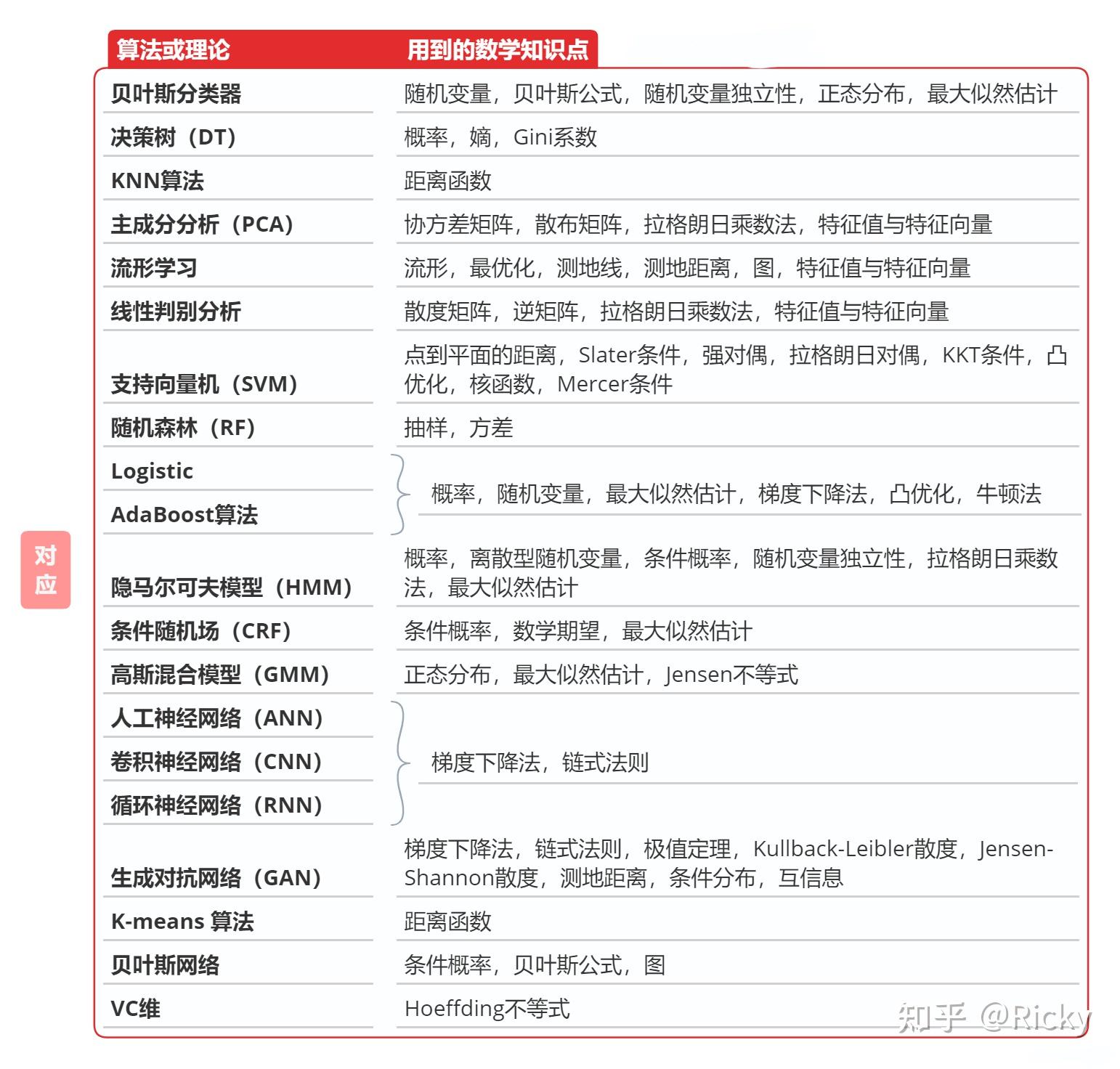
图片来自：https://zhuanlan.zhihu.com/p/541807727

由图可以看到,

出现频率最高的是优化方法：拉格朗日乘数法、梯度下降法、牛顿法、凸优化.

其次是概率论知识：随机变量、贝叶斯公式、随机变量独立性、正太分布、最大似然估计

再次是线性代数知识，几乎所有都会涉及到：向量、矩阵、张量、特征值和特征向量。很多算法都会最终变成求解特征值和特征向量问题。

然后是微积分的知识比如链式法则。

除此之外，还会用到微分几何中的流行、测地线、测地距离的概念。支持向量机会用到 Mercer 条件、核函数，涉及到泛函分析和识别函数的范畴。

再比如说人工神经网络的证明，万能逼近定理会用到泛函分析和识别函数的内容，用来证明这样一个函数可以来逼近任何形式的函数。

离散数学的知识比如图论、树在机器学习里面也会用到，但是用的都是比较简单的。

所以只有掌握好微积分、线性代数、概率论还有一些优化的算法，我们就能看懂所有的机器学习算法。像刚才说的一些相对高深的微分几何、泛函分析和识别函数，它们主要用在一些基础理论证明上面，即使看不懂这些证明，也并不影响你理解这些算法的推导、思想和使用。