IJCAI 2019
1 abstract & intro
- 时空数据挖掘问题大多数使用邻接矩阵来建模节点之间的属性关系,这种思路的一个基本假设是:节点信息取决于自身和邻居的历史信息。
- 但这类模型的假设存在着一些问题:
- 未能充分建模节点之间的依赖关系
- 两个节点之间没有连边,但是有依赖关系
- 两个节点虽然是邻居节点,但是没有依赖关系
- 未能有效学习到时间的依赖关系
- RNN:迭代传播耗时(无法并行)、存在梯度爆炸/消失的问题
- CNN:需要迭代很多层,才能得到较大的感受野
- 未能充分建模节点之间的依赖关系
- 但这类模型的假设存在着一些问题:
- ——>这篇论文提出graph Wavenet,使用自适应的邻接矩阵,在没有先验知识的情况下建模节点的空间依赖关系;同时使用扩散图卷积+空洞卷积,来解决第二个问题
2 问题定义
- 给定图G=(V,E),其中节点集V,边集合E
- 邻接矩阵为
- 在某一时间步t,输入的节点信号矩阵是
- 邻接矩阵为
- 这篇论文的目标和一般的时空数据预测类似,给定图G和过去S步的图信号数据,预测接下来T步的图信号
3 模型部分
3.1 自适应扩散图卷积(空间依赖关系)
- 无向图的扩散图卷积
,表示某个点转移到其他点的概率
- 有向图的扩散图卷积
,表示某个点转移到其他节点的概率(正向扩散)
,表示某个节点从其他节点转移过来的概率(反向扩散)
- 上面两个主要是DCRNN的思路【论文笔记:DCRNN (Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting)_UQI-LIUWJ的博客-CSDN博客】,本篇论文的highlight是首次引入了自适应图结构的概念,公式如下:
- E1和E2是随机初始化的两个节点的embedding(以METR-LA为例,METR-LA有207个节点,代码 里 E1 、E2维度分别均是 (207,10))
- 分别表示每个点作为源节点和目标节点之间的空间依赖权重
- 使用Relu消除自适应邻接矩阵中的弱连接
- 使用Softmax归一化自适应邻接矩阵
- E1和E2是随机初始化的两个节点的embedding(以METR-LA为例,METR-LA有207个节点,代码 里 E1 、E2维度分别均是 (207,10))
- ——>可以将归一化的自适应邻接矩阵视为隐藏扩散过程的转换矩阵‘
- 结合预定义的空间依赖关系和自适应的隐藏空间依赖关系,就有了如下的图卷积
- 如果事先没有预定义的空间依赖关系,那么只使用自适应图卷积
3.2 时间卷积网络(时间依赖性)
使用空洞因果卷积 (dilated causal convolution)来捕获时间趋势
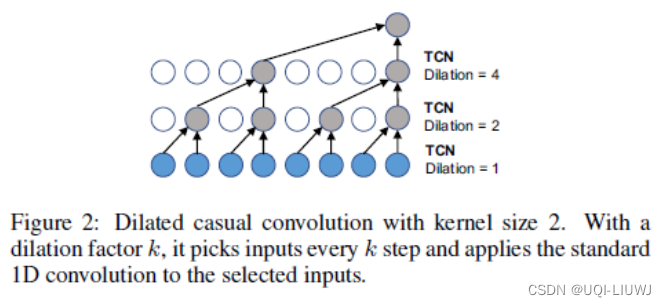
3.2.1 门控TCN
3.3 整体模型
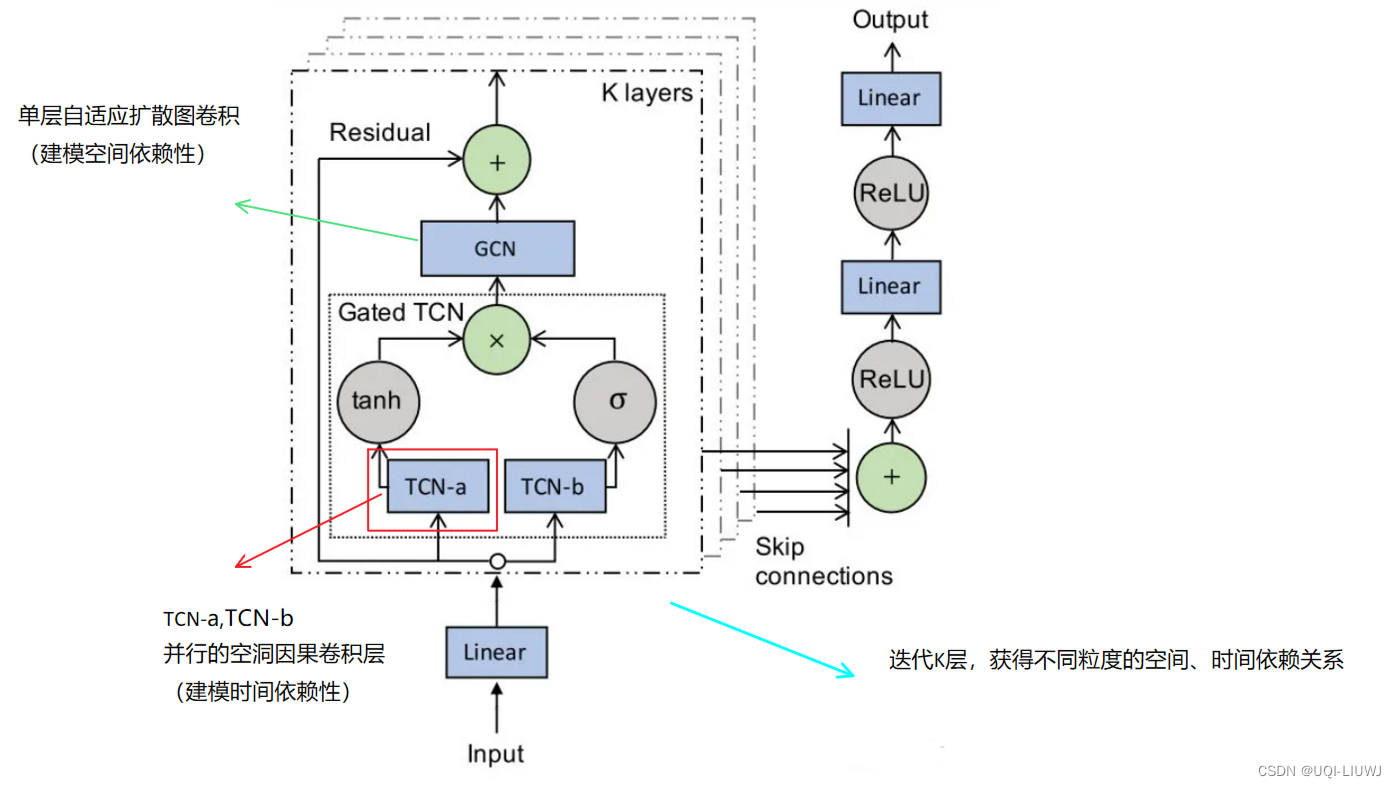
4 实验部分
4.1 不同模型对比
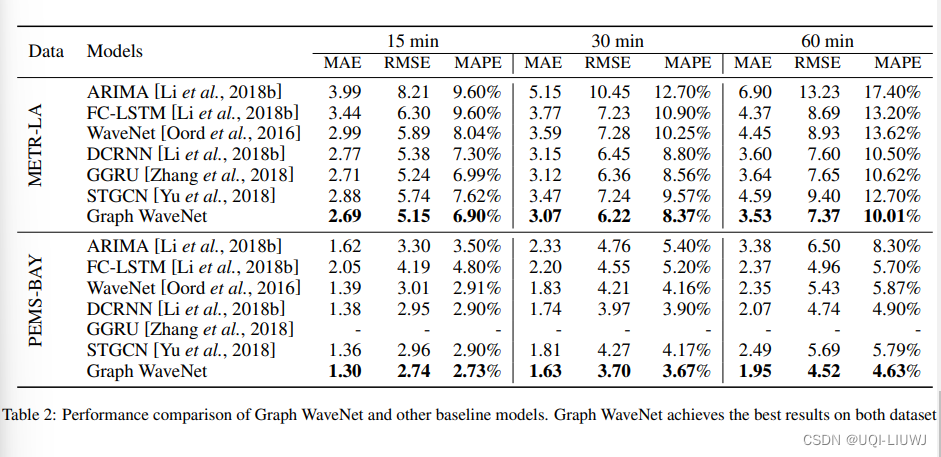
4.2 不同邻接矩阵构造方式对比
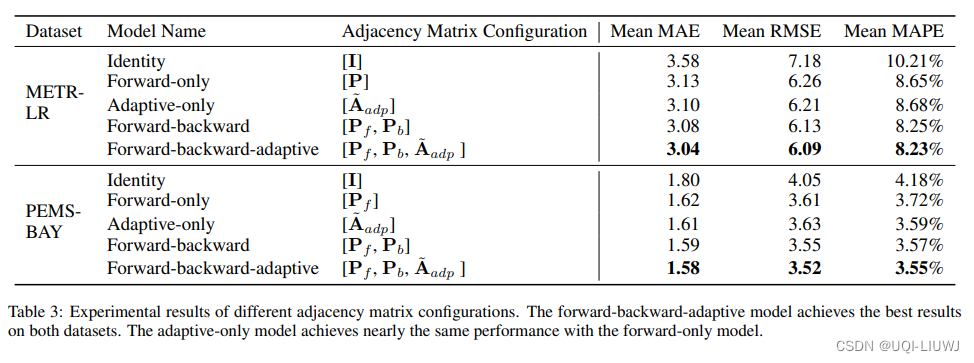
4.3 自适应邻接矩阵可视化
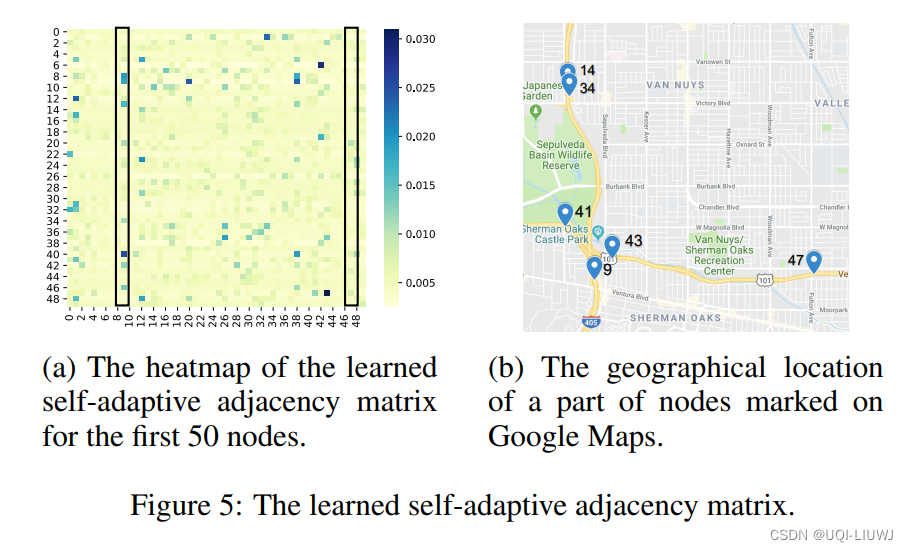
论文比较了9号节点和47号节点,通过左图可以发现,9号节点这一列有值的要多一些:9号节点和更多的其他节点有影响:通过右图可以发现,确实9号节点在交叉口,47号节点就“偏远”了很多
4.4 预测结果可视化
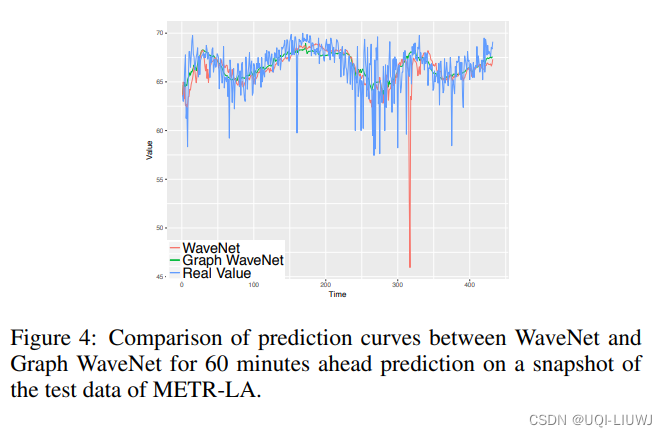
graph wavenet和真实值更贴切一些
4.5 计算时间
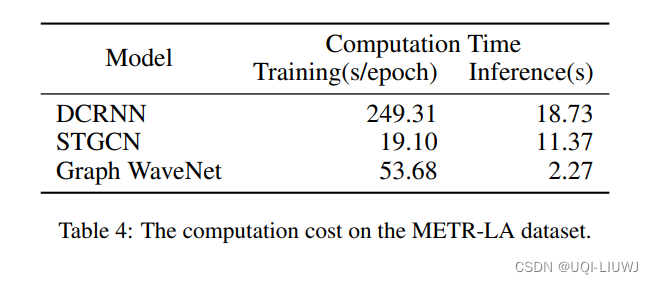
- Training的话,Graph WaveNet需要多训练两个embedding E1和E2,所以会稍微慢一些
- 但是在inference阶段,graph wave是使用空洞卷积来进行预测的,可以一次性预测很多个未来的时间片;而DCRNN和STGCN都是使用RNN的,需要一个一个时间片迭代,故Graph WaveNet会快一些





![[LeetCode]2319. 判断矩阵是否是一个 X 矩阵](https://img-blog.csdnimg.cn/img_convert/a7398d2e17da5473878d8b72610aff55.jpeg)