题目

104、二叉树的最大深度

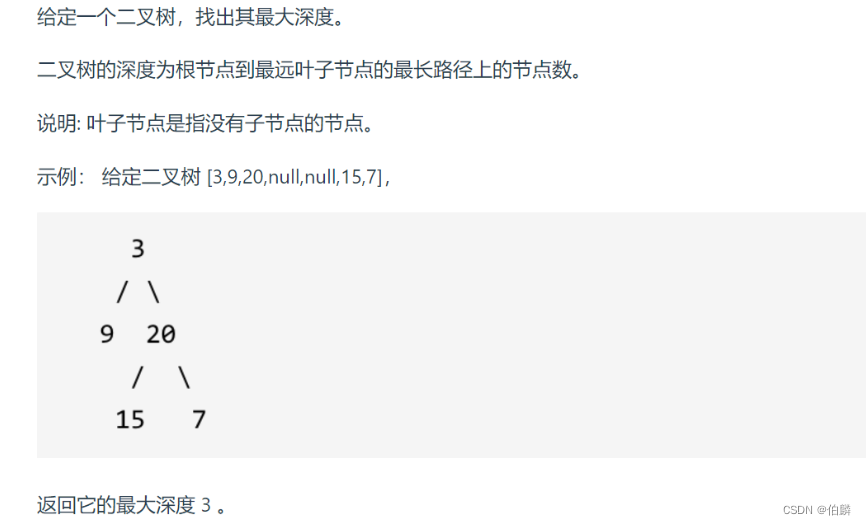
递归法（后序）（必须会）

// 定义：输入根节点，返回这棵二叉树的最大深度
int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // 利用定义，计算左右子树的最大深度
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    // 整棵树的最大深度等于左右子树的最大深度取最大值，
    // 然后再加上根节点自己
    int res = Math.max(leftMax, rightMax) + 1;

    return res;
}

迭代法（层序）（必须会）

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null)   return 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        int depth = 0;
        while (!que.isEmpty())
        {
            int len = que.size();
            while (len > 0)
            {
                TreeNode node = que.poll();
                if (node.left != null)  que.offer(node.left);
                if (node.right != null) que.offer(node.right);
                len--;
            }
            depth++;
        }
        return depth;
    }
}

111、二叉树的最小深度

迭代法（层序）

class Solution {
    public int minDepth(TreeNode root) {
        if(root==null)
            return 0;
        
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        int depth = 0;
        while(!q.isEmpty()){
            int sz = q.size();
            depth+=1;
            for(int i=0;i<sz;i++){
                TreeNode cur = q.poll();
                if(cur.left==null && cur.right==null)
                    return depth;
                if(cur.left!=null)
                    q.offer(cur.left);
                if(cur.right!=null)
                    q.offer(cur.right);
            }
        }
        return depth;
    }
}

递归法（复杂一些）

如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。
反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。
遍历的顺序为后序（左右中），可以看出：求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

class Solution {
    /**
     * 递归法，相比求MaxDepth要复杂点
     * 因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量
     */
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        if (root.left == null) {
            return rightDepth + 1;
        }
        if (root.right == null) {
            return leftDepth + 1;
        }
        // 左右结点都不为null
        return Math.min(leftDepth, rightDepth) + 1;
    }
}

222、完全二叉树的节点个数

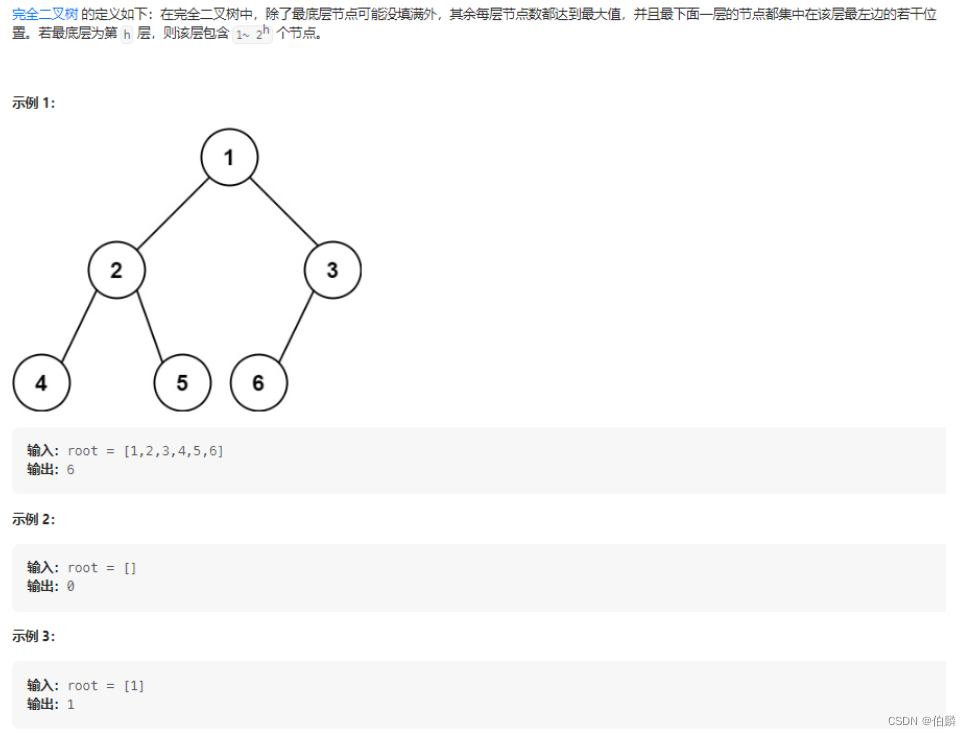
递归法

class Solution {
    public int countNodes(TreeNode root) {
        if(root==null) return 0;
        int leftNum = countNodes(root.left);
        int rightNum = countNodes(root.right);
        return leftNum+rightNum+1;
    }
}

迭代法（层序）

class Solution {
    // 迭代法
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for(int i=0;i<size;i++){
                TreeNode cur = queue.poll();
                result++;
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }
}

平衡二叉树

递归法
此时大家应该明白了既然要求比较高度，必然是要后序遍历。

递归三步曲分析：

• 1、明确递归函数的参数和返回值
  参数：当前传入节点。
  返回值：以当前传入节点为根节点的树的高度。
  那么如何标记左右子树是否差值大于1呢？
  如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。
  代码如下：
  // -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
  int getHeight(TreeNode* node)
• 2、明确终止条件
  递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
  代码如下：
  if(root==null) return 0;
• 3、明确单层递归的逻辑
  如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。
  分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。