洪水是暴雨、急剧融冰化雪、风暴潮等自然因素引起的江河湖泊水量迅速增加,或者水位迅猛上涨的一种自然现象,是自然灾害。洪水又称大水,是河流、海洋、湖泊等水体上涨超过一定水位,威胁有关地区的安全,甚至造成灾害的水流。洪水一词,在中国出自先秦《尚书·尧典》。从那时起,四千多年中有过很多次水灾记载,欧洲最早的洪水记载也远在公元前1450年。在西亚的底格里斯一幼发拉底河以及非洲的尼罗河关于洪水的记载,则可追溯到公元前40世纪。2023年6月24日8时至25 日8时,中国15条河流发生超警洪水。2023年,全球洪水等造成了数十亿美元的经济损失。
洪水的频率和严重程度与人口增长趋势相当一致。迅猛的人口增长,扩大耕地,围湖造田,乱砍滥伐等人为破坏不断地改变着地表状态,改变了汇流条件,加剧了洪灾程度。在降水多的年份,洪水是否造成灾害,以及洪水灾害的大小,也离不开人为因素,长期以来人为的森林破坏是其重要原因。长江上游乱砍滥伐的恶果是惊人的水土流失。现已达 35 万平方千米,每年土壤漫融量达25 亿吨。河流、湖泊、水库淤积的泥沙量达 20 亿吨。仅四川一省一年流入长江各支流的泥沙,如叠成宽高各】米的堤,可以围绕地球赤道16圈。我国第一大淡水湖洞庭湖每年沉积的泥沙达】亿多吃,有专家惊呼:“这样下去,要不了50年,洞庭湖将从地球上消失!”长江之险,险在荆江,由于泥沙俱下,如今荆江段河床比江外地面高出十多米,成了除黄河之外名副其实的地上河。对森林的肆意砍伐不仅危害自己,而且祸及子孙后代,世界上许多地方,如美索不达米亚、小亚细亚、阿尔卑斯山南坡等由于过度砍伐森林,最后都变成了不毛之地。附件 train,csv 中提供了超过100万的洪水数据,其中包含洪水事件的 id、季风强度、地形排水、河流管理、森林砍伐、城市化、气候变化、大坝质量、淤积、农业实践、侵蚀、无效防灾、排水系统、海岸脆弱性、滑坡、流城、基础设施恶化、人口得分、湿地损失、规划不足、政策因素和发生洪水的概率。附件test.csv中包含了超过70万的洪水数据,其中包含洪水事件的id和上述 20个指标得分,缺少发生洪水的概率。附件submi.csv 中包含 test.csv 中的洪水事件的 id,缺少发生洪水的概率。
请你们的团队通过数学建模和数据分析的方法,预测发生洪水灾害的概率,解决以下问题:
问题 1. 请分析附件 train.csv 中的数据,分析并可视化上述 20 个指标中,哪些指标与洪水的发生有着密切的关联?哪些指标与洪水发生的相关性不大?并分析可能的原因,然后针对洪水的提前预防,提出你们合理的建议和措施。(完整见文末附件!)
洪水是由多种因素共同作用的复杂自然灾害事件。为了系统地分析这些因素对洪水发生的影响,我们需要建立数学模型,量化各个因素与洪水发生概率之间的关系。以下是详细的数学建模过程及其预防措施。
-
数据准备 首先,数据集中包含20个指标(独立变量)和洪水发生的概率(目标变量)。设 xi 表示第i个样本,其中 xi=(xi1,xi2,...,xi20),yi表示第i个样本的洪水发生概率。
-
相关性分析 我们需要计算每个独立变量与目标变量之间的相关性。通常使用皮尔逊相关系数来衡量线性相关性。皮尔逊相关系数r的公式为:
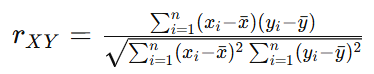
-
多元线性回归模型 为了进一步量化各个指标对洪水发生概率的影响,我们可以使用多元线性回归模型。多元线性回归模型假设洪水发生概率y可以表示为各个指标 xi 的线性组合:
![]()
其中,β0是截距项,βi是第i个指标的回归系数,ϵ是误差项。 我们可以使用最小二乘法(OLS)来估计回归系数 βi。OLS 的目标是最小化残差平方和:
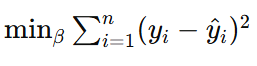
其中,y^i是预测值:
-
模型评价与选择
模型建立后,我们需要评估模型的性能。常用的评价指标包括决定系数 R2和均方误差(MSE):
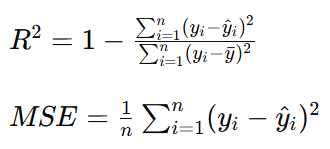
通过这些指标,我们可以判断模型的拟合优度和预测精度。

问题 2.将附件 train.csv 中洪水发生的概率聚类成不同类别,分析具有高中、低风险的洪水事件的指标特征。然后,选取合适的指标,计算不同指标的权重,建立发生洪水不同风险的预警评价模型,最后进行模型的灵敏度分析。
洪水是自然灾害中最常见的类型之一,其发生具有高度的不确定性和复杂性。为了有效分析和预测洪水风险,我们需要对洪水发生的概率进行聚类分析,识别高、中、低风险类别,并建立预警评价模型。以下是详细的数学建模过程及其相关公式。
-
数据准备与标准化 假设数据集包含 n个样本,每个样本有 m个指标(独立变量)和洪水发生的概率(目标变量)。设 X=[x1,x2,...,xn]T表示数据矩阵,其中 xi=(xi1,xi2,...,xim)为第 iii 个样本的指标向量,yi表示第 iii 个样本的洪水发生概率。 为了使不同尺度的指标具有可比性,我们需要对数据进行标准化处理。标准化公式为:
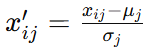
其中,xij表示第i个样本的第j个指标,μ和 σj分别表示第j个指标的均值和标准差。
-
聚类分析 为了将洪水发生概率聚类成不同的风险类别,我们可以使用K-means 聚类算法。设K 为预定的聚类数目,我们希望将数据集划分为K个聚类,使得同一聚类中的样本在特征空间中的距离最小,而不同聚类间的样本距离最大。 K-means 聚类的目标函数为:
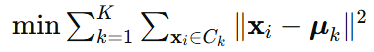
其中,Ck表示第 k个聚类,μk为第k个聚类的中心。
-
指标特征分析 通过聚类分析,我们将样本划分为 KKK 个风险类别。对于每个风险类别Ck,我们可以计算各个指标的均值来分析其特征。设 xˉkj表示第 kkk 个风险类别中第j个指标的均值,计算公式为:
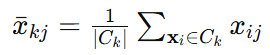
通过比较不同风险类别的均值,我们可以识别高、中、低风险类别的主要特征。
-
指标权重计算 为了进一步量化各个指标对洪水发生风险的影响,我们需要计算不同指标的权重。可以使用随机森林回归模型来评估各个指标的重要性。随机森林的重要性度量基于每个指标对预测结果的不纯度减少量(Gini impurity 或均方误差)。 设Ij表示第j个指标的重要性,计算公式为:
![]()
其中,TTT 是树的总数,ΔIjt表示第t棵树中第j个指标的不纯度减少量。
-
建立预警评价模型 基于计算的指标权重,我们可以建立洪水风险的预警评价模型。假设我们使用线性回归模型来建立预警模型,模型形式为:
![]()
其中,β0是截距项,βj是第j个指标的回归系数。 使用最小二乘法(OLS)估计回归系数,目标是最小化残差平方和:
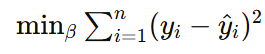
其中,y^i是预测值:
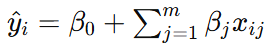
-
模型评价 为了评估预警模型的性能,我们可以使用均方误差(MSE)和决定系数(R2)等指标。均方误差的计算公式为:
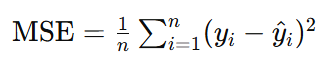
决定系数 R2的计算公式为:
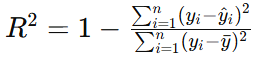
其中,yˉ是目标变量y的均值。
-
模型灵敏度分析
为了分析预警模型对不同指标变化的敏感性,我们可以使用排列重要性(Permutation Importance)方法。排列重要性通过随机打乱一个指标的值来评估该指标对模型性能的影响。
设 Ij表示第aj个指标的排列重要性,计算公式为:
![]()
其中,y^i,j是打乱第j个指标后得到的预测值。
代码求解结果:


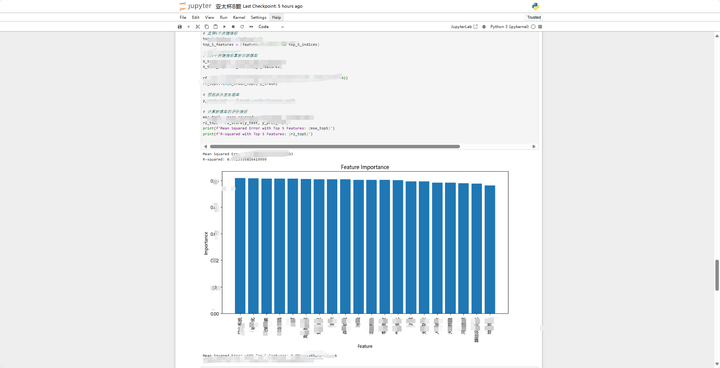
问题3.基于问题1中指标分析的结果,请建立洪水发生概率的预测模型从 20个指标中选取合适指标,预测洪水发生的概率,并验证你们预测模型的准确性。如果仅用5个关键指标,如何调整改进你们的洪水发生概率的预测模型?
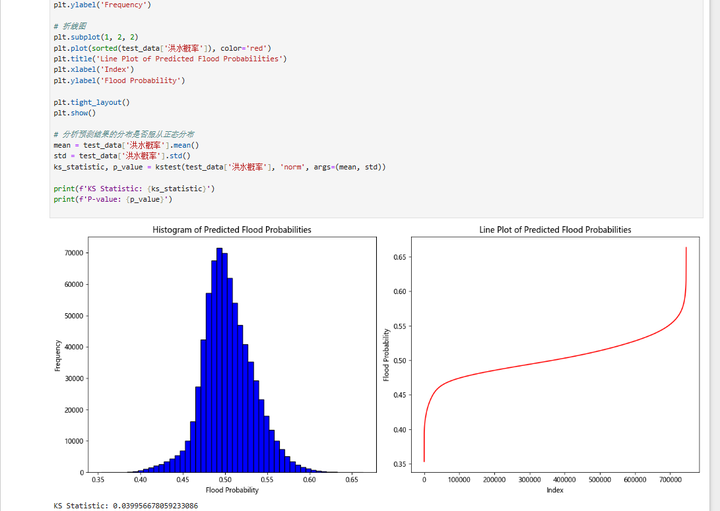
问题4.基于问题2中建立的洪水发生概率的预测模型,预测附件 test.csv 中所有事件发生洪水的概率,并将预测结果填入附件 submit.csv 中。然后绘制这 74多万件发生洪水的概率的直方图和折线图,分析此结果的分布是否服从正态分布

完整版本获取: