大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
抱个拳,送个礼
预警:今天文章的描述可能会让你有点别扭;如感到不适,请及时停止
在我行走江湖的行囊中,有两件利器,tableau与matplotlib,它们足以让我应对各种数据可视化的较量。tableau,乃是BI领域的名门正派,其可视化之术,与PowerBI不相上下。matplotlib,则是Python江湖中的一位侠客,以编程之力,绘制图表,既精妙又实用。


防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3

更多内容,见免费知识星球
Tableau
Tableau,乃斯坦福大学之奇才所铸,一款软件中的绝世神兵。它助你以神速分析世间所有结构化数据,转瞬之间,便能绘制出美轮美奂的图表、坐标图、仪表盘与报告。
Tableau之界面,简易而不失精妙,一拖一放,便能随心所欲地定制视图、布局、形状、色彩,让你的数据以独特的视角展现于世。
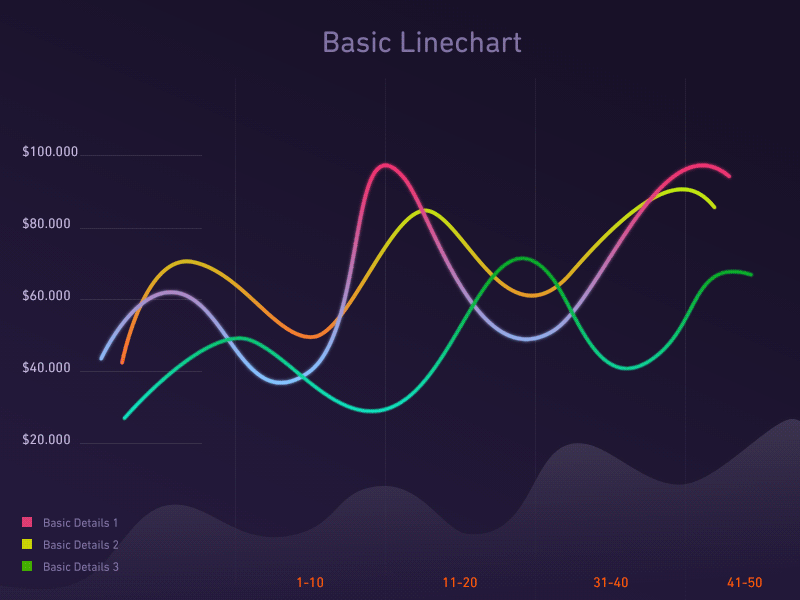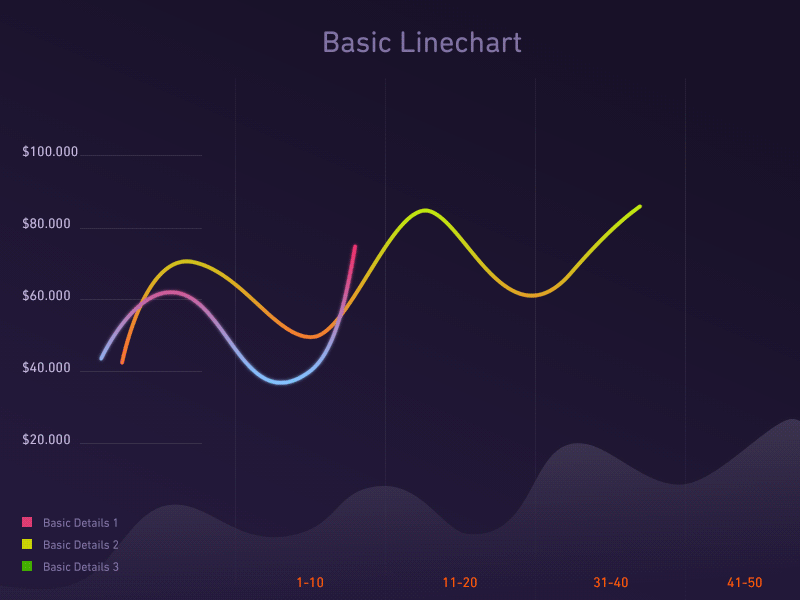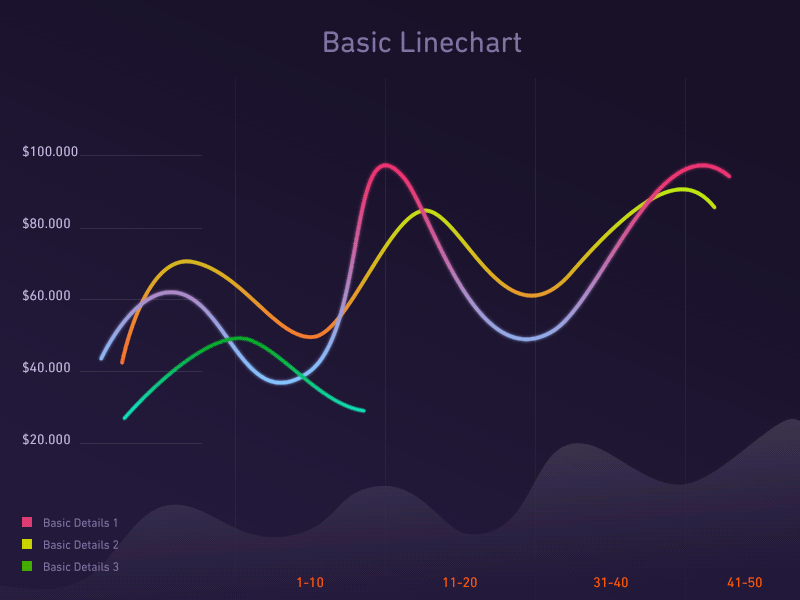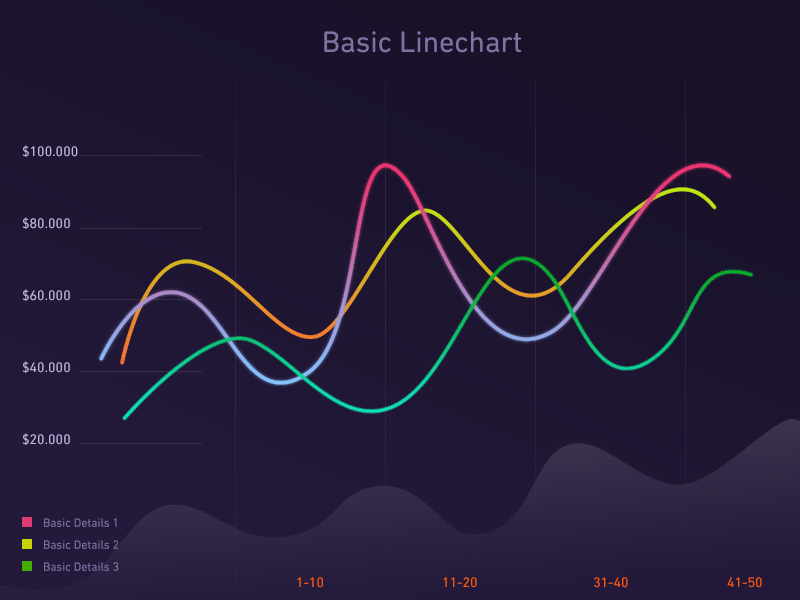
1. 趋势图
趋势图,乃是洞察数据走势的利器。
折线图,如同江湖中的轻功,轻盈地勾勒出数据的连续变化;
柱形图,如同武林中的剑法,一剑一剑地刻画出事件的演变;
堆积图,如同内功的修炼,层层累积地展现出部分的比重及其变化之势。
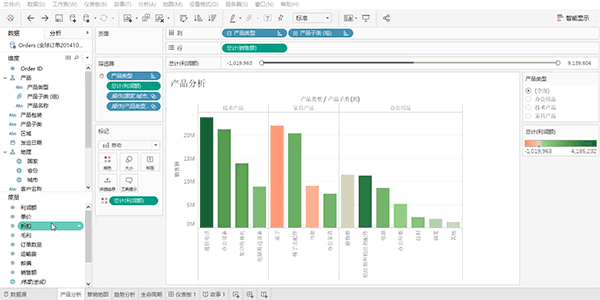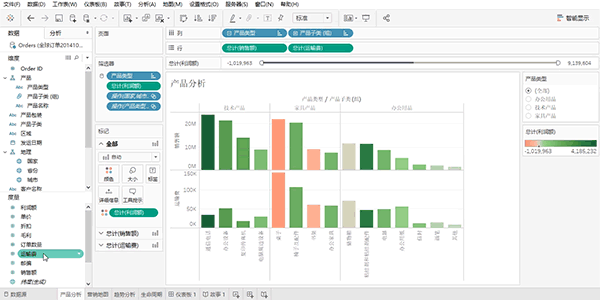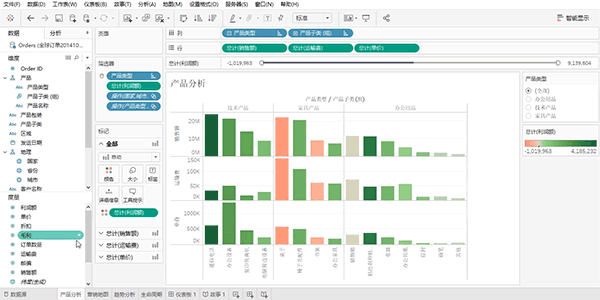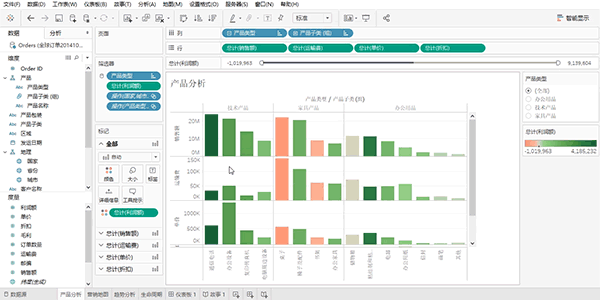
2. 频数图
频数图,是武林中人比较武艺高低的法宝。
柱形图与条形图,如同比武场上的裁判,一柱一柱、一条一条地将各项目数值的高低清晰展现。
借助频数图,观者可迅速洞察各数值之强弱,一目了然
3. 结构图
结构图,乃是洞察数据内部结构的秘籍。
饼图、圆环图、树图、旭日图,这些图表如同内功心法,一层层地揭示出各部分在整体中的比重。
借助这些图,你便能如观内功脉络一般,清晰地看到数据的骨架和比例。

4. 分布图
分布图,乃是探查数据分布奥秘的法宝。
柱形图与条形图,如同武林高手的剑招,一柱一条地描绘出数据的分布;
散点图,如同满天星斗,点缀着数据的分布点;
地图,如同江湖地图,将数据的分布情况在大地之上一一标示出来。



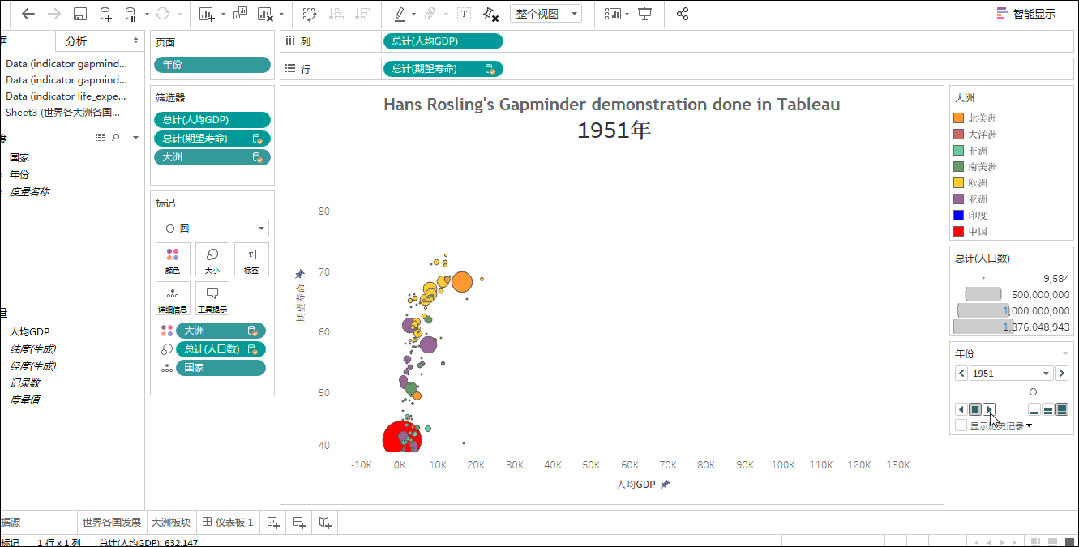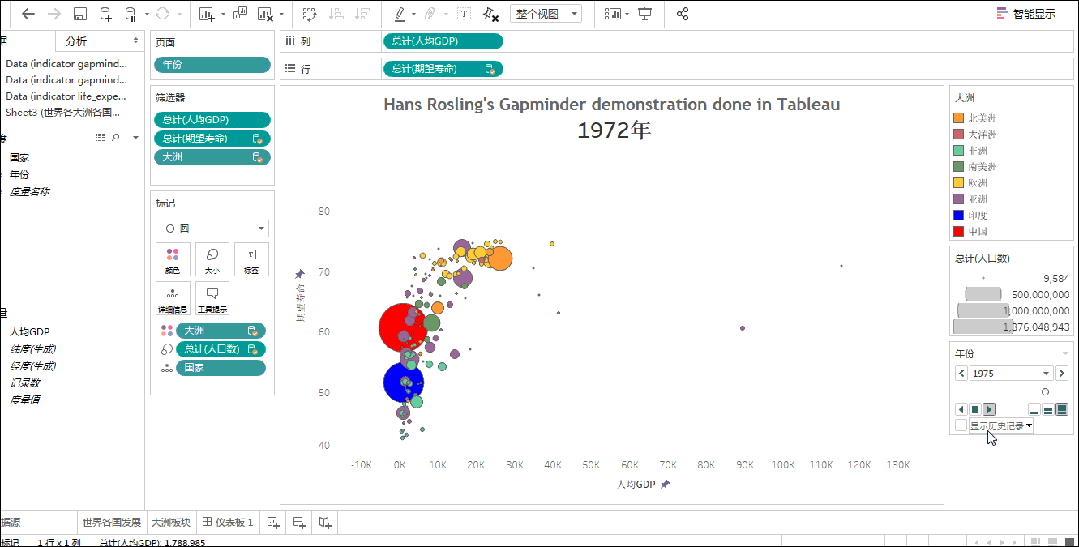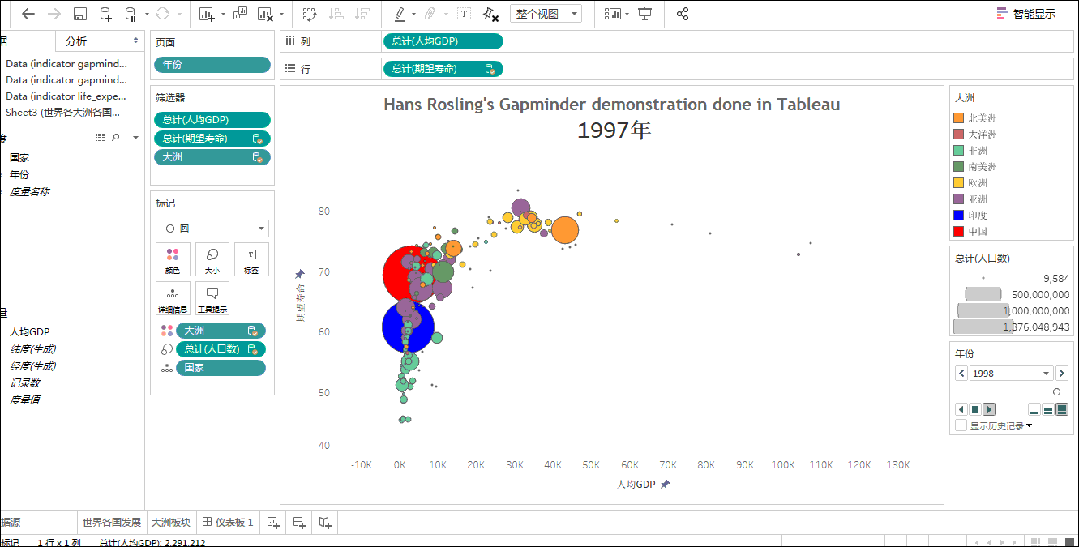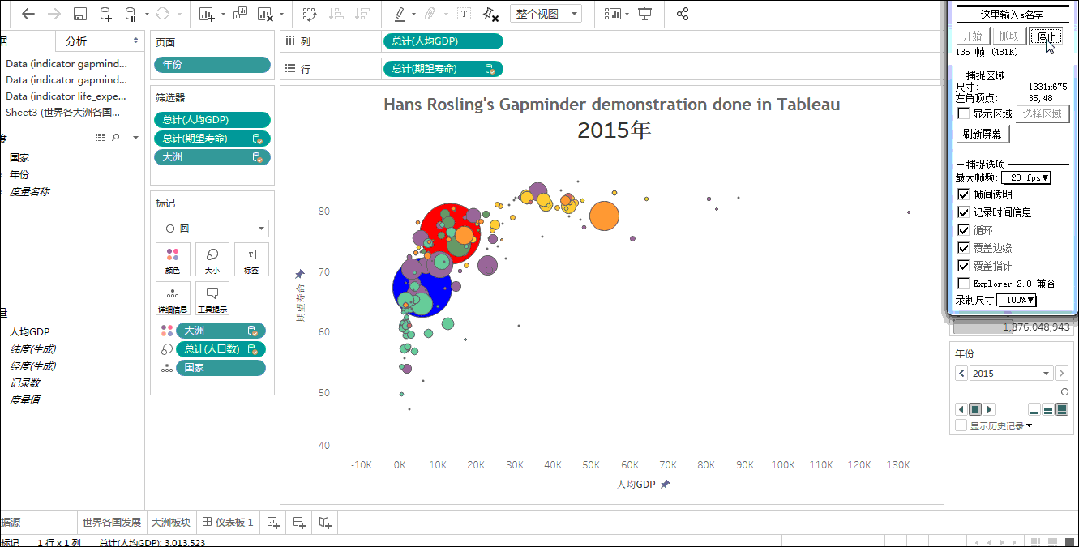
5. 相关图
相关图,乃是洞察数据间关联的秘籍。
散点图,如同武林中人观察对手的招式,一点一滴地揭示出数据间的联系;
气泡图,如同江湖中的暗器,大小不一地展现出数据间关系的紧密程度。
借助这些图,你便能如武林高手般洞悉数据间的微妙关系。
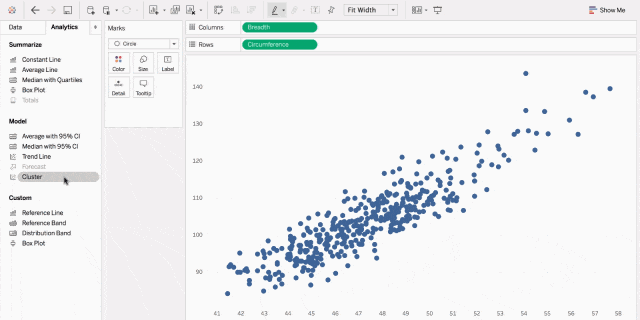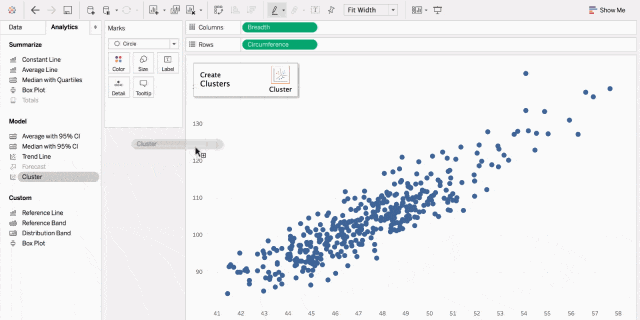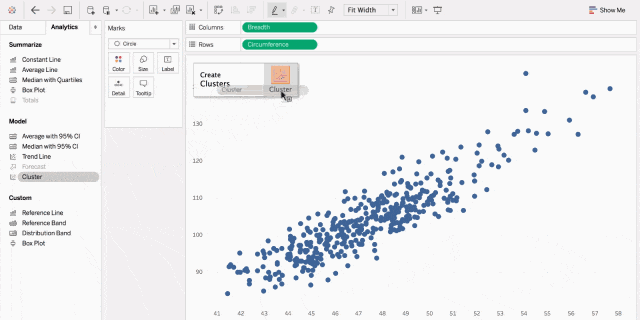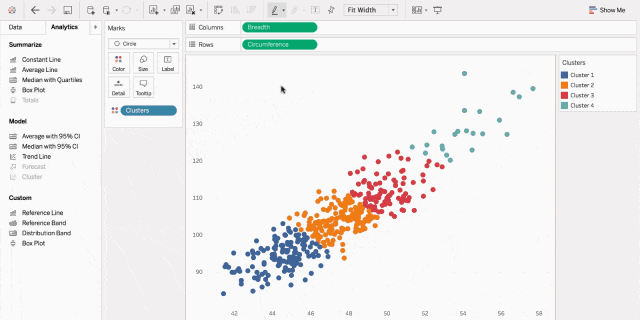

抱个拳,送个礼
点击 ↑ 领取
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3
免费知识星球,欢迎加入交流
Matplotlib
Matplotlib,与tableau迥异,乃是Python武林中一位专精于绘图的高手。
它非同小可,乃是众多绘图库中最为强大、最为常用的存在。
诸如seaborn、cartoony等门派,皆以matplotlib为基石,依赖其深厚的内力。
Matplotlib,此乃2003年由John D. Hunter首次公诸于世的绘图秘籍。历经十数载的磨砺与完善,如今已成为Python科学可视化的不二法门。
它曾助力展示黑洞之神秘影像,亦曾阐释引力波之存在。
Matplotlib之图,由众多层次分明的元素构成,遵循构图之逻辑,层层叠加,终成眼前所见之实际图形,宛若江湖高手以掌法绘制的阵图。
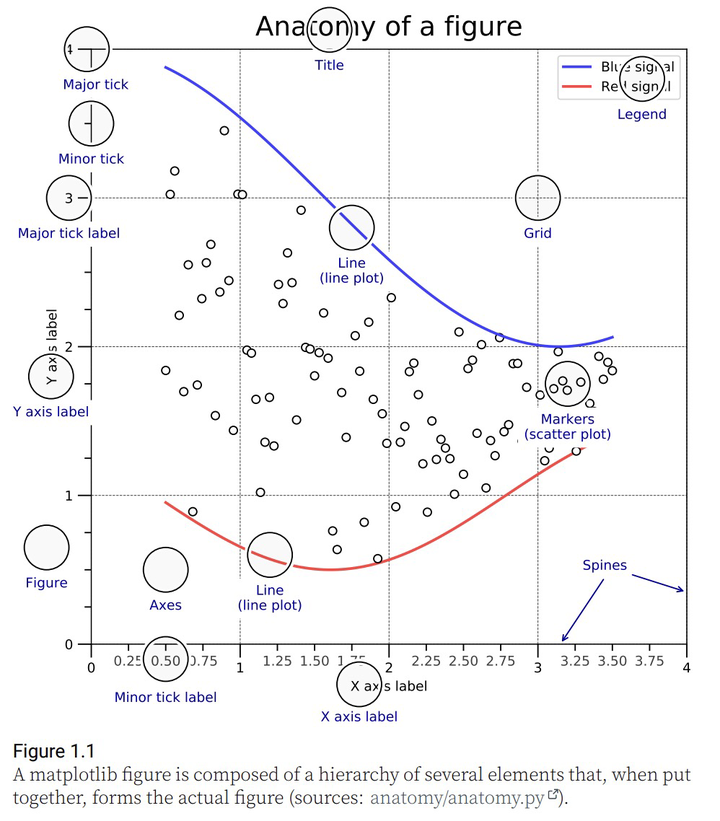
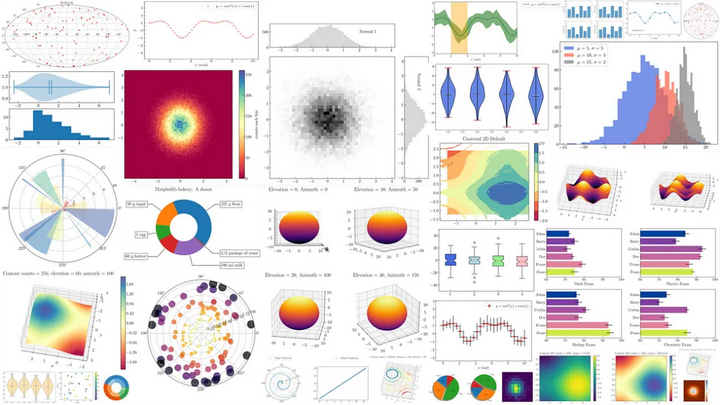

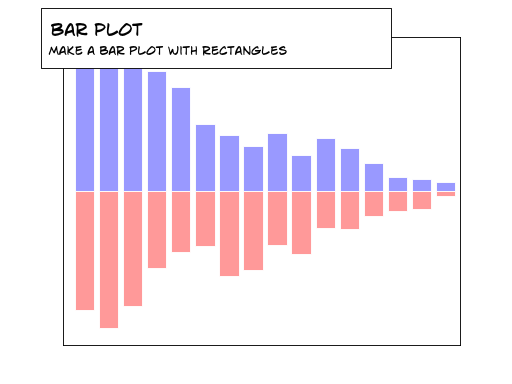
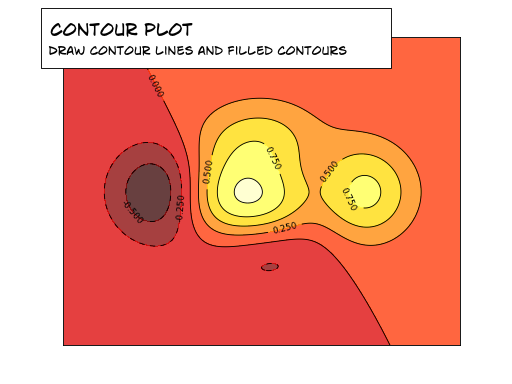

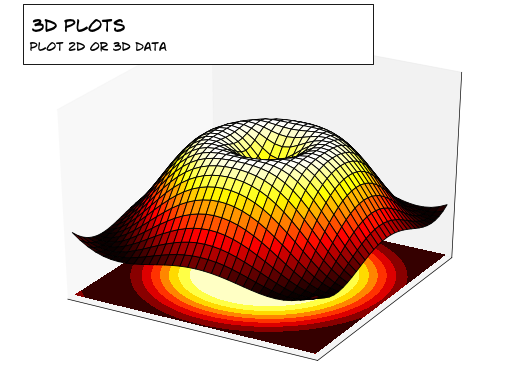

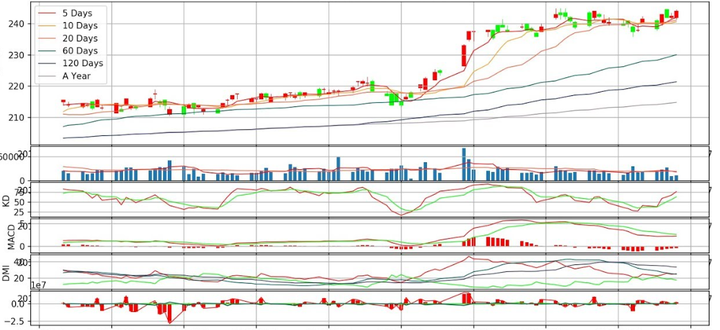
Matplotlib,此乃绘图之利器,不仅可用于科学可视化,亦能绘制股市之K线图。使用Matplotlib绘制K线图,便捷之至,宛如江湖中人随手拈来的绝技。
对于量化监测而言,它便是那得心应手的神兵利器。
[ 抱个拳,总个结 ]
- 科研为国分忧,创新与民造福 -

日更时间紧任务急,难免有疏漏之处,还请大侠海涵 内容仅供学习交流之用,部分素材来自网络,侵联删
[ 算法金,碎碎念 ]
太热了,这儿说的是天气
知了都来了,一只,两只
承包了我们家今天的快乐
崽崽激动得半夜还睡不着


全网同名,日更万日,让更多人享受智能乐趣
如果觉得内容有价值,烦请大侠多多 分享、在看、点赞,助力算法金又猛又持久、很黄很 BL 的日更下去;
同时邀请大侠 关注、星标 算法金,围观日更万日,助你功力大增、笑傲江湖