0 结果

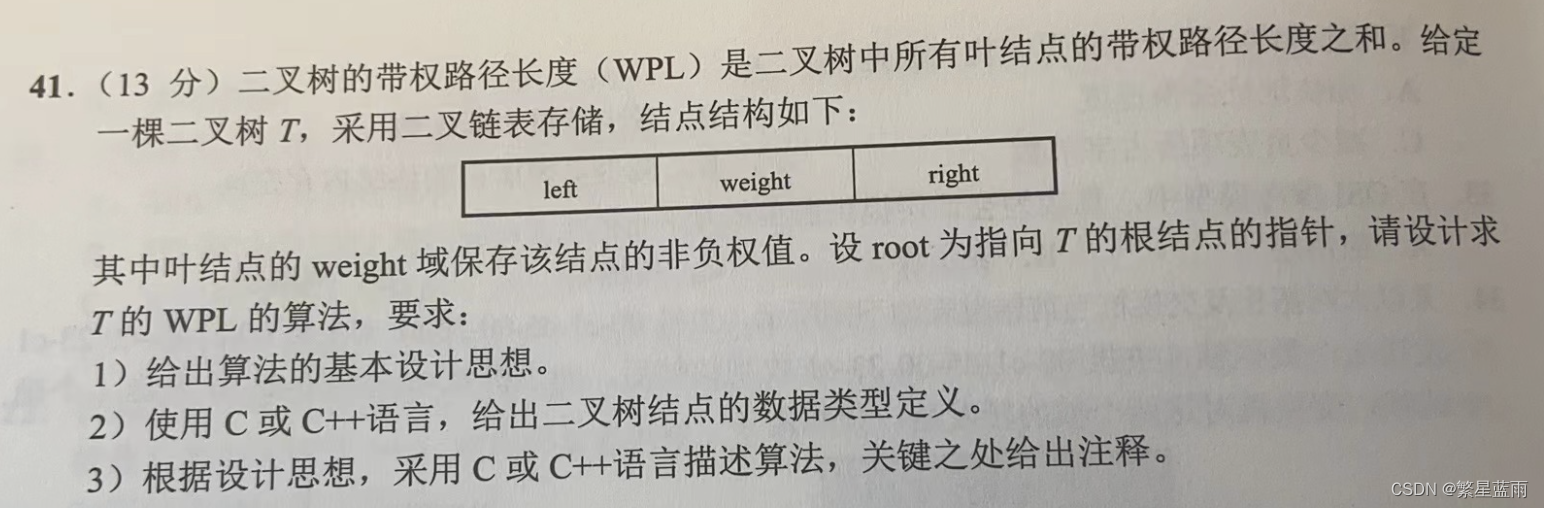
请添加图片描述

1 题目

请添加图片描述

2 思路

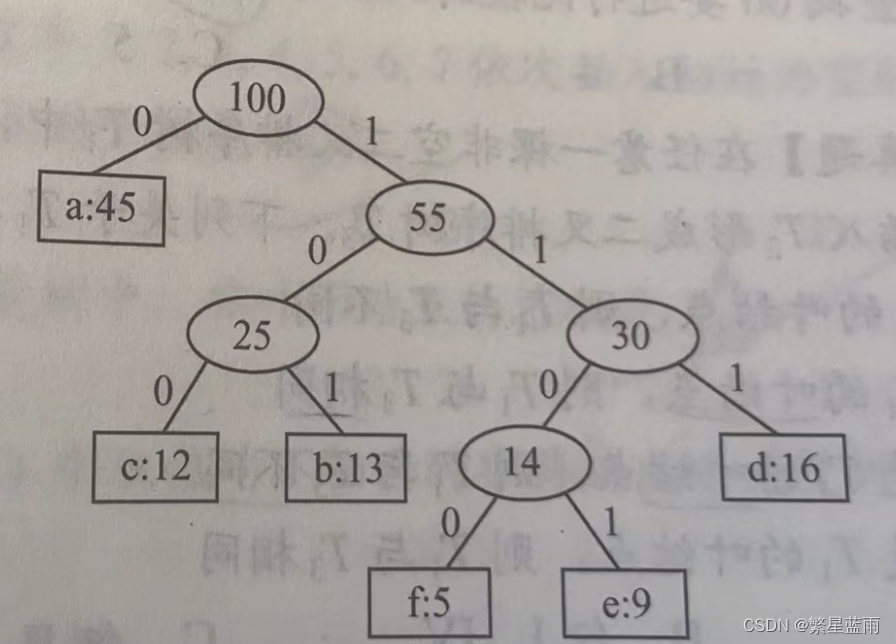
二叉树的带权路径长度（WPL）的计算方法有两种：

1，定义： $WPL=所有叶结点的权值W_i*该结点深度D_i求和$ 。
2，在哈夫曼树中， $W P L = 所有非叶结点的权值和$ 。

本题只能使用方法1，代码如下所示：

#include <cstdio>
#include <cstdlib>
#include <vector>
using std::vector;

typedef struct BTNode{
    int weight;
    struct  BTNode *left, *right;
}BTNode;

int WPL = 0;

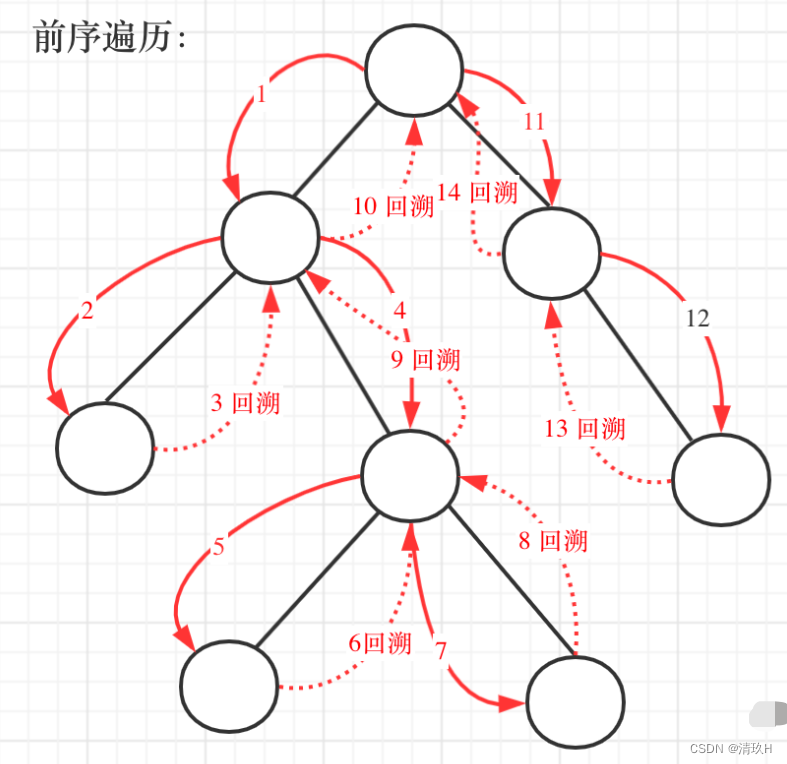
//前序遍历
void preOrder(BTNode* p, int d){//d:深度
    if(p == nullptr) return;
    if(p->left == nullptr && p->right == nullptr)//叶结点
        WPL += d*p->weight;
    preOrder(p->left, d + 1);
    preOrder(p->right, d + 1);
}

void ans(BTNode* root){
    preOrder(root, 0);
}

//中序序列
int in[] = {45, 100, 12, 25, 13, 55, 5, 14, 9, 30, 16};
//根据中序和层序创建二叉树
BTNode* Create4(vector<int> layer, int inL, int inR){
    if(layer.size() == 0){//当前层序遍历完
        return NULL;
    }

    BTNode* root = new BTNode;
    root->weight = layer[0];

    int k;
    for (k = inL; k <= inR; ++k) {//中序序列中寻找根结点
        if(in[k] == root->weight){
            break;
        }
    }

    vector<int> leftLayer;//左子树层次遍历
    vector<int> rightLayer;//右子树层次遍历

    for (int i = 1; i < layer.size(); ++i) {//遍历层序序列，分左右子树存储
        bool isLeft = false;
        for (int j = inL; j < k; ++j) {
            if(layer[i] == in[j]){
                isLeft = true;
                break;
            }
        }
        if(isLeft == true){
            leftLayer.push_back(layer[i]);
        }else{
            rightLayer.push_back(layer[i]);
        }
    }

    root->left = Create4(leftLayer,inL, k - 1);
    root->right = Create4(rightLayer,k + 1, inR);

    return root;
}

int main(){
    vector<int> layer;//中序序列
    layer.push_back(100);
    layer.push_back(45);
    layer.push_back(55);
    layer.push_back(25);
    layer.push_back(30);
    layer.push_back(12);
    layer.push_back(13);
    layer.push_back(14);
    layer.push_back(16);
    layer.push_back(5);
    layer.push_back(9);

    BTNode * root  = Create4(layer,  0, sizeof(in)/sizeof(in[0]));
    ans(root);
    printf("%d", WPL);

    return 0;
}