2023.1.31
超参数是指神经网络中,神经元的数量、batch的大小、参数更新时的学习率或权值衰减等,虽然超参数的取值非常重要,但是决定超参数的值时会伴随很多人工的试错,所以我们需要高效地寻找超参数的值的方法
一,验证数据:
验证数据也称为验证集,用于调整超参数的数值,评估超参数的好坏,确认泛化能力。
前面的学习中,我们将数据分成训练集、测试集,训练数据用于神经网络权重、偏置的学习,测试数据用于评估神经网络模型的泛化能力(由此就可以评估神经网络模型是否出现过拟合现象)。
因为要防止神经网络模型出现过拟合现象,所以测试数据不能用训练数据去充当;同理,也不能用测试数据去充当验证数据。因此,用测试数据去确认超参数的好坏,就会导致超参数的值被调整只为拟合测试数据,这样,可能导致神经网络模型的泛化能力低下。
在对神经网络模型进行实验的过程中,我们需要将数据集分成 训练集、测试集、验证集,有的只会被分成训练集和测试集,这个时候我们就需要自行对数据集进行分割。
以之前用来学习的MNIST数据集为例子,为了获得验证数据,可以在训练数据中抽出20%再打乱顺序作为测试数据;
代码如下:
from dataset.mnist import load_mnist
import numpy as np
def shuffle_dataset(x, t):
permutation = np.random.permutation(x.shape[0])
# np.random.permutation( ) 总体来说他是一个随机排列函数,就是将输入的数据进行随机排列
x = x[permutation, :] if x.ndim == 2 else x[permutation, :, :, :]
t = t[permutation]
return x, t
(x_train, t_train), (x_test, t_test) = load_mnist()
x_train, t_train = shuffle_dataset(x_train, t_train)
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]关于打乱数组顺序的操作,可以参考这篇文章:【Numpy】中np.random.shuffle()与np.random.permutation()的用法和区别_Amelie_xiao的博客-CSDN博客_np.random.shuffle对给定的数组进行重新排列的方式主要有两种:np.random.shuffle(x) :在原数组上进行,改变自身序列,无返回值。np.random…permutation(x) :不在原数组上进行,返回新的数组,不改变自身数组。1. np.random.shuffle(x)1. 对一维数组重新排序:import numpy as nparr = np.arange(10)print(arr)np.random.shuffle(arr)print(arr)2. 对多维数组重新.
https://blog.csdn.net/lemonxiaoxiao/article/details/109239996
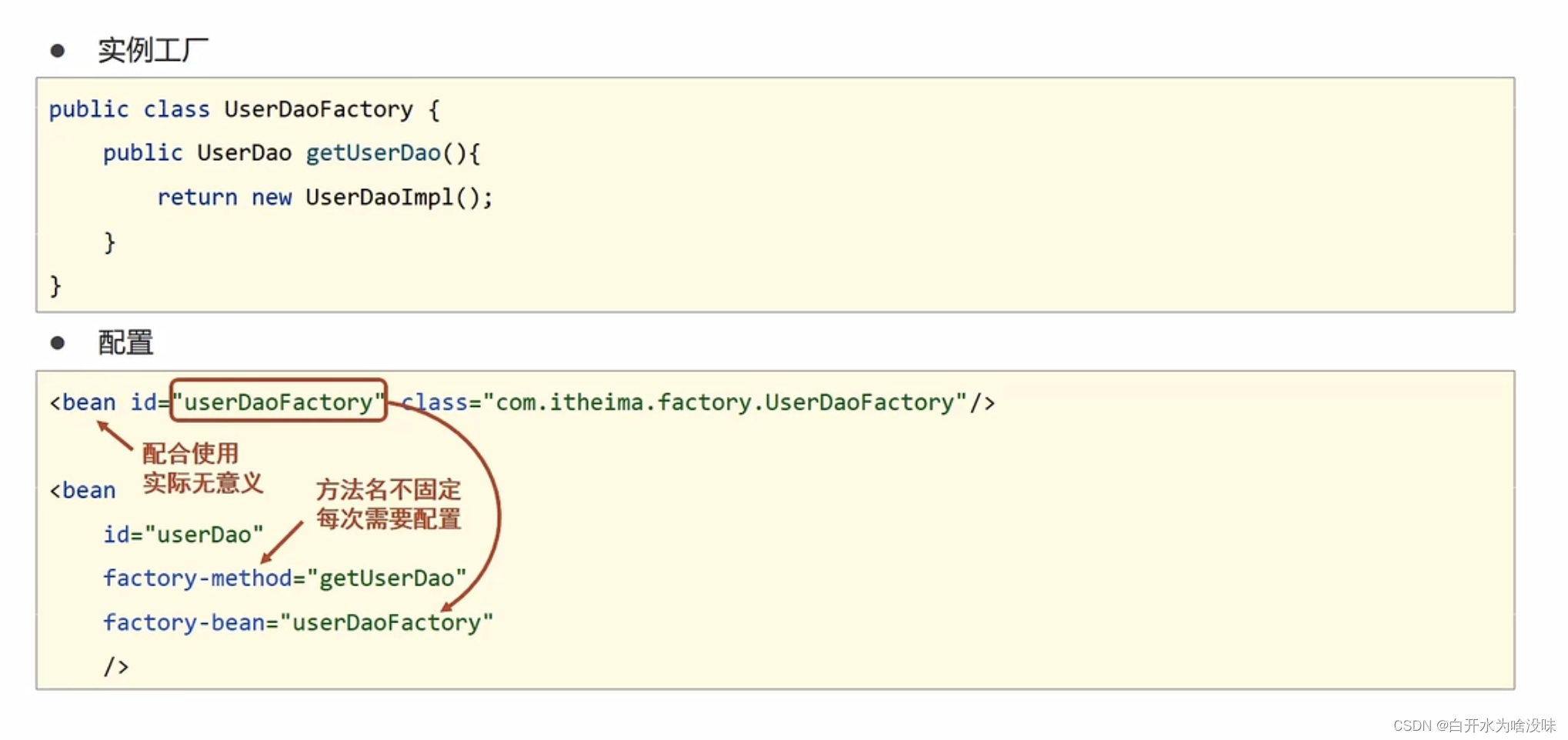
二,超参数的最优化:
进行超参数的最优化时,逐渐缩小超参数的“最佳值”的存在范围非常重要。
所谓“缩小范围”是指一开始先大致设定一个范围,从这个范围中随机采样一个超参数,用这个采样到值进行识别精度的评估;然后,多次重复这样的操作,观察识别精度的结果。
超参数优化的步骤:
步骤1:
设定超参数范围;只要大致确定就行了,像用对数尺度 到
这样就好了;
步骤2:
从设定的范围中随机采样;教材提到过,在神经网络的超参数最优化时,与网格搜索等有规律的搜索相比,随机采样的搜索方式效果更好。这是因为在多个超参数中,各个超参数对最终的识别精度的影响程度不同。
步骤3:
使用步骤2中的采样的超参数进行学习,通过验证集评估识别精度;由于深度学习需要花费很长时间,因此在超参数的搜索中,我们也要放弃那些不符合逻辑的超参数。于是,减少epoch,缩短一个评估的时间,会更有效率的完成优化;
步骤4:
重复步骤2和步骤3,根据他们的识别精度的结果,缩小超参数的范围;
这样方法是一种实践性的方法,并不是很精炼;当然有一个更加有效率的方法 贝叶斯最优化
三、超参数最优化的实现:
这里利用MNIST数据集进行超参数的最优化,依照上述步骤进行操作;
这里称学习率与控制权衰减强度的系数为“权重衰减系数”;
在python中实现超参数范围的决定:
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -4)
print(weight_decay, lr)
关于np.random.uniform( ) 函数的使用,可以参考文章:
numpy.random.uniform() - AI大道理 - 博客园
之后就是进行随机采样后,再使用这些值进行学习,之后,多次使用各种超参数进行学习,观察实验结果
实验代码(来自教材):
from dataset.mnist import load_mnist
import numpy as np
from collections import OrderedDict
import sys, os
import matplotlib.pyplot as plt
sys.path.append(os.pardir)
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
class Nesterov:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x)
return np.exp(x) / np.sum(np.exp(x))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 权重和偏置参数的导数
self.dW = None
self.db = None
def forward(self, x):
# 对应张量
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None # softmax的输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
class MultiLayerNet:
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.weight_decay_lambda = weight_decay_lambda
self.params = {}
# 初始化权重
self.__init_weight(weight_init_std)
# 生成层
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict()
for idx in range(1, self.hidden_layer_num + 1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1]) # 使用ReLU的情况下推荐的初始值
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1]) # 使用sigmoid的情况下推荐的初始值
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx - 1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1: t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers[
'Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
class Trainer:
"""进行神经网络的训练的类
"""
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr': 0.01},
evaluate_sample_num_per_epoch=None, verbose=True):
self.network = network
self.verbose = verbose
self.x_train = x_train
self.t_train = t_train
self.x_test = x_test
self.t_test = t_test
self.epochs = epochs
self.batch_size = mini_batch_size
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
# optimzer
optimizer_class_dict = {'sgd': SGD, 'momentum': Momentum, 'nesterov': Nesterov,
'adagrad': AdaGrad, 'rmsprpo': RMSprop, 'adam': Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)
self.train_size = x_train.shape[0]
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
self.max_iter = int(epochs * self.iter_per_epoch)
self.current_iter = 0
self.current_epoch = 0
self.train_loss_list = []
self.train_acc_list = []
self.test_acc_list = []
def train_step(self):
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
grads = self.network.gradient(x_batch, t_batch)
self.optimizer.update(self.network.params, grads)
loss = self.network.loss(x_batch, t_batch)
self.train_loss_list.append(loss)
if self.verbose: print("train loss:" + str(loss))
if self.current_iter % self.iter_per_epoch == 0:
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print(
"=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(
test_acc) + " ===")
self.current_iter += 1
def train(self):
for i in range(self.max_iter):
self.train_step()
test_acc = self.network.accuracy(self.x_test, self.t_test)
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))
def shuffle_dataset(x, t):
permutation = np.random.permutation(x.shape[0])
# np.random.permutation( ) 总体来说他是一个随机排列函数,就是将输入的数据进行随机排列
x = x[permutation, :] if x.ndim == 2 else x[permutation, :, :, :]
t = t[permutation]
return x, t
# 为了实现高速化,减少训练数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
x_train = x_train[:500]
t_train = t_train[:500]
# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
# Droput 集成学习
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
# 超参数的随机搜索
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 指定搜索的超参数的范围
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
val_acc_list, train_acc_list = __train(lr, weight_decay)
print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
# 绘制图形 选择20个验证集正确率最高的作图,观察结果
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
for key, val_acc_list in sorted(results_val.items(), key=lambda x: x[1][-1], reverse=True):
print("Best-" + str(i + 1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i + 1)
plt.title("Best-" + str(i + 1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()
观察实验结果:
=========== Hyper-Parameter Optimization Result ===========
Best-1(val acc:0.81) | lr:0.007750951715862939, weight decay:2.1846853690857217e-07
Best-2(val acc:0.81) | lr:0.00838130050967965, weight decay:1.1598298306613237e-05
Best-3(val acc:0.8) | lr:0.00876075374155661, weight decay:5.976935213257307e-07
Best-4(val acc:0.8) | lr:0.007815268011397574, weight decay:1.575522514559289e-07
Best-5(val acc:0.79) | lr:0.009654948479826187, weight decay:3.285293252728692e-08
Best-6(val acc:0.77) | lr:0.007036898447730358, weight decay:5.01196097094863e-07
Best-7(val acc:0.76) | lr:0.007029405514595431, weight decay:9.697616555985926e-07
Best-8(val acc:0.74) | lr:0.005914444614230039, weight decay:2.2430128356259564e-05
Best-9(val acc:0.69) | lr:0.0044728273595469, weight decay:3.936982750904726e-06
Best-10(val acc:0.65) | lr:0.005423073089401118, weight decay:2.9232270845687685e-05
Best-11(val acc:0.63) | lr:0.004923641765280372, weight decay:1.8432769973117267e-05
Best-12(val acc:0.62) | lr:0.004341263117334942, weight decay:2.968820491705765e-07
Best-13(val acc:0.57) | lr:0.0040604306735793246, weight decay:1.4796486034937558e-07
Best-14(val acc:0.5) | lr:0.0037773977352559803, weight decay:4.333232959678954e-07
Best-15(val acc:0.39) | lr:0.0021076338689053602, weight decay:7.632875965383985e-05
Best-16(val acc:0.37) | lr:0.0028195930917857583, weight decay:6.352468012321727e-08
Best-17(val acc:0.35) | lr:0.0028660152947906775, weight decay:1.6708839837464746e-05
Best-18(val acc:0.33) | lr:0.0019621452082444184, weight decay:4.096061802503812e-08
Best-19(val acc:0.33) | lr:0.001838016553154147, weight decay:9.594189356124086e-05
Best-20(val acc:0.33) | lr:0.002214804091793635, weight decay:8.157270927085107e-05Process finished with exit code 0
按识别精度从高到底排序,虚线是验证数据的识别精度、实线是训练数据的识别精度;
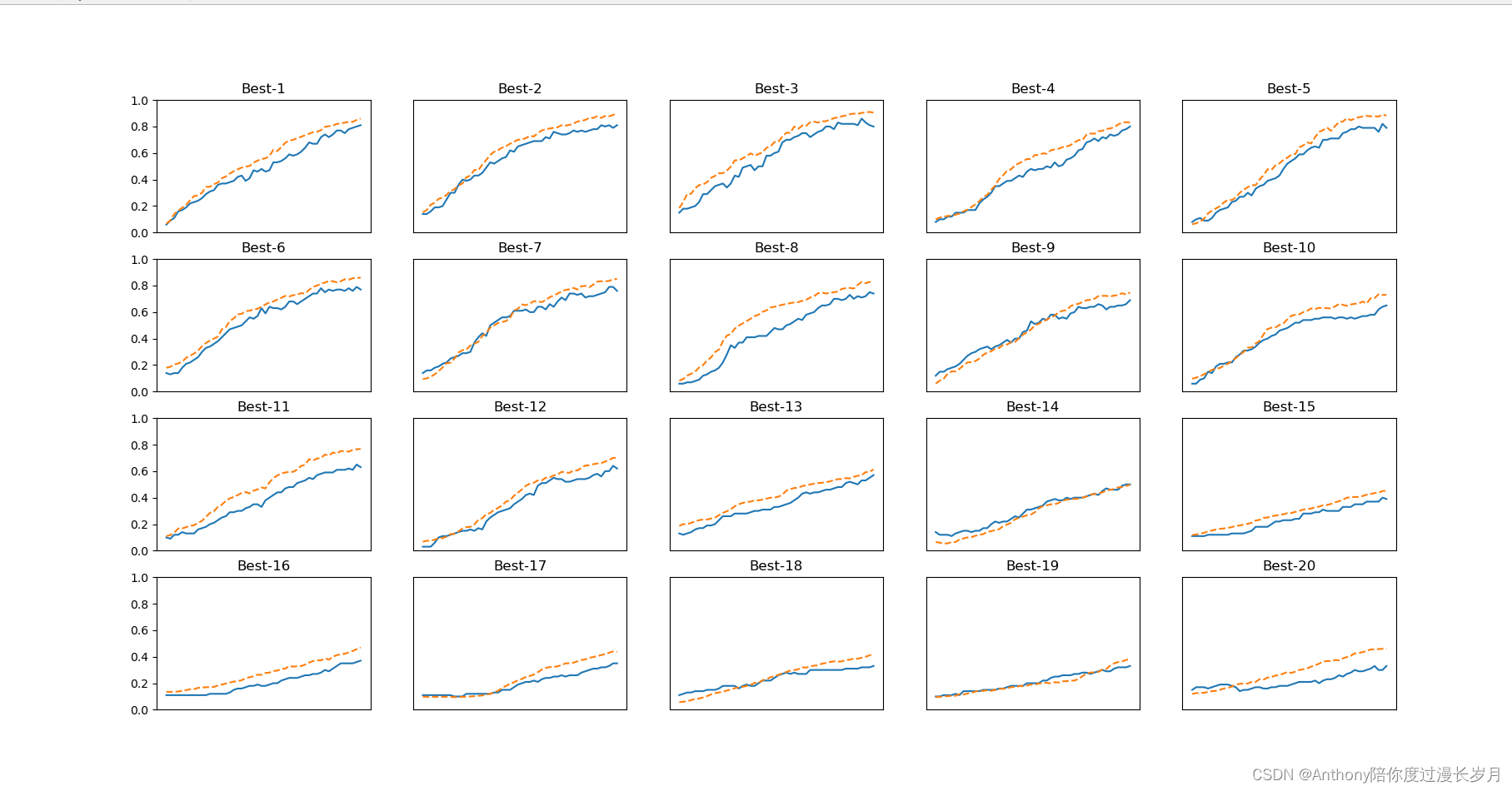
从这个结果可以看出,学习率0.001到0.01、权值衰减系数在 到
之间时,学习可以顺利进行。然后我们可以在此基础上缩小值的范围,重复相同的操作;这样就能缩小适合的超参数的存在范围,然后选择一个最佳的值。
四,MNIST数据集的导入:
代码需要在一个命名为命名为dataset的文件夹下命名为mnist,并且与实验代码在同一个文件夹;
# coding: utf-8
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img':'train-images-idx3-ubyte.gz',
'train_label':'train-labels-idx1-ubyte.gz',
'test_img':'t10k-images-idx3-ubyte.gz',
'test_label':'t10k-labels-idx1-ubyte.gz'
}
dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
"""读入MNIST数据集
Parameters
----------
normalize : 将图像的像素值正规化为0.0~1.0
one_hot_label :
one_hot_label为True的情况下,标签作为one-hot数组返回
one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
flatten : 是否将图像展开为一维数组
Returns
-------
(训练图像, 训练标签), (测试图像, 测试标签)
"""
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
if __name__ == '__main__':
init_mnist()