【算法自由之路】二叉树的递归套路
预热,二叉树的后继节点
话不多说,首先是一道练手题,寻找二叉树任意给定节点的后继节点,此二叉树具备一个指向父节点的指针。
后继节点:在中序遍历中于给定节点后一个打印的节点
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public TreeNode(int val) {
this.val = val;
}
}
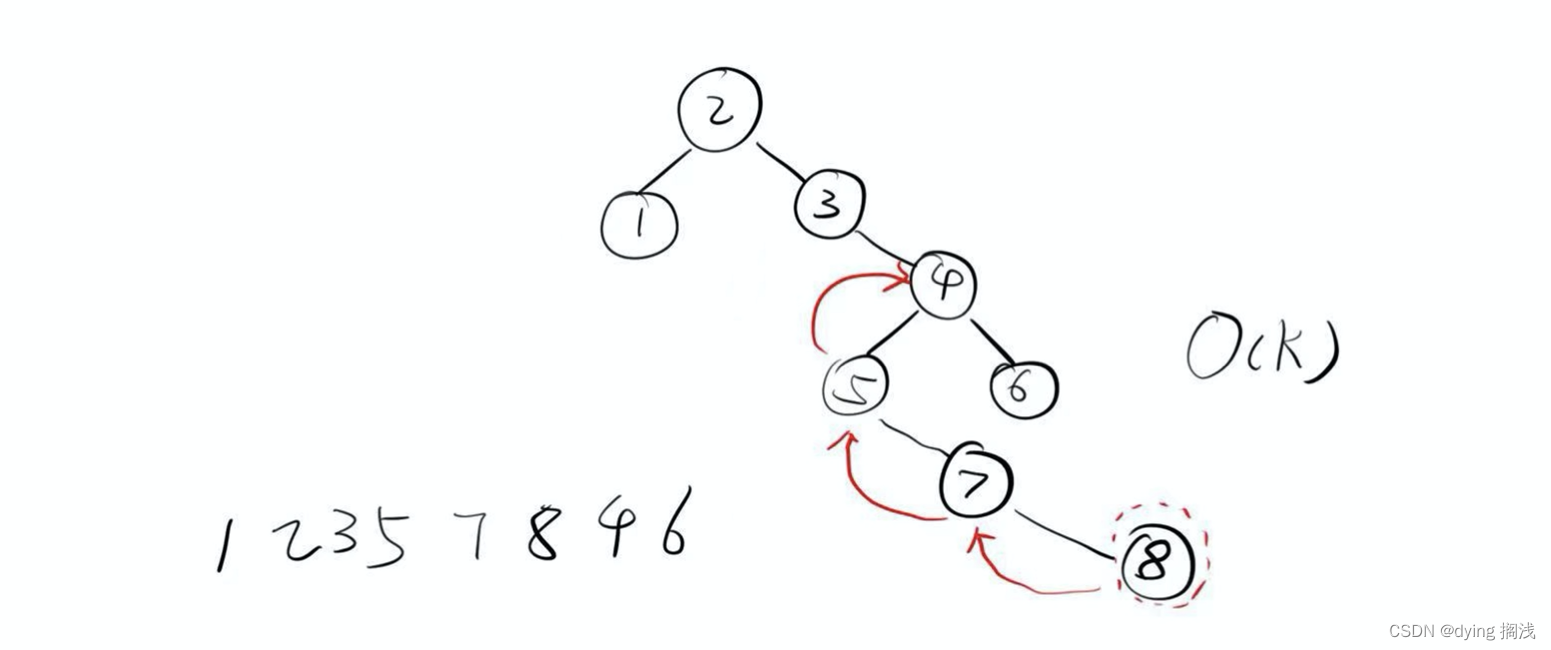
这道题其实主要考验的是分类讨论和找规律的能力。首先理解中序遍历对每个子树打印顺序都是 左 中 右。比如下图这个树
做分类讨论其实就两个情况:
- 该节点有右节点:后继为右节点的最左节点
- 该节点没有右节点:后继节点为向上找,第一次子节点是父节点的左孩子的父节点,比如 8 的后继就是 4
对于情况 2 我们其实可以反推来理解, 4 节点的前驱节点应该是 左子树的最右的一个节点。
package algorithmic.base.tree;
/**
* @program: algorithmic-total-solution
* @description: 查找二叉树的后继节点,
* @author: wangzibin
* @create: 2023-01-10
**/
public class FindNextNode {
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public TreeNode(int val) {
this.val = val;
}
@Override
public String toString() {
return "TreeNode{" +
"val=" + val +
'}';
}
}
public static void print(TreeNode node) {
if (node == null) {
return;
}
print(node.left);
System.out.print(node.val);
print(node.right);
}
public static TreeNode findNextNode(TreeNode node) {
if (node == null) {
return null;
}
TreeNode result = null;
// 如果有右孩子,后继节点是右孩子的最左节点
if (node.right != null) {
result = node.right;
while (result.left != null) {
result = result.left;
}
return result;
}
// 如果没有右孩子,向上找第一个子孩子是左节点的父节点 (有点绕,看代码)
result = node.parent;
// 注意最右节点没有后继节点
while (node.parent != null && node != result.left) {
node = node.parent;
result = node.parent;
}
return result;
}
public static void main(String[] args) {
TreeNode head = new TreeNode(2);
TreeNode node1 = new TreeNode(1);
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
TreeNode node7 = new TreeNode(7);
TreeNode node8 = new TreeNode(8);
head.left = node1;
node1.parent = head;
head.right = node3;
node3.parent = head;
node3.right = node4;
node4.parent = node3;
node4.left = node5;
node5.parent = node4;
node4.right = node6;
node6.parent = node4;
node5.right = node7;
node7.parent = node5;
node7.right = node8;
node8.parent = node7;
print(head);
System.out.println();
System.out.println(findNextNode(node1));
System.out.println(findNextNode(head));
System.out.println(findNextNode(node3));
System.out.println(findNextNode(node5));
System.out.println(findNextNode(node7));
System.out.println(findNextNode(node8));
System.out.println(findNextNode(node4));
System.out.println(findNextNode(node6));
}
}
递归套路
二叉树的递归套路有点像拆分子任务,将要求的最终结果分给每个分支去做
在实际应用中,对于一个整个树的问题,假设可以向左右子树要任何信息,整合信息后得出最终结果
整个拆分任务的操作我们交给了堆栈去做
递归套路 1 判断一个二叉树是平衡二叉树
平衡二叉树定义:对于树中任意一个节点,其左子树和右子树的高度差不超过 1。
这里假设我可以向左右子树获取任何信息,那对于判断我是否是平衡二叉树的关系信息是:
- 子树高度
- 子树是否是平衡二叉树
于是我可以定义这样一个返回结构
public static class NodeInfo {
public boolean isBalanced;
public int high;
public NodeInfo(boolean isBalanced, int high) {
this.isBalanced = isBalanced;
this.high = high;
}
}
最终代码很简单
public class BalanceTree {
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public static class NodeInfo {
public boolean isBalanced;
public int high;
public NodeInfo(boolean isBalanced, int high) {
this.isBalanced = isBalanced;
this.high = high;
}
}
public boolean isBalanced(TreeNode root) {
return getNodeInfo(root).isBalanced;
}
public NodeInfo getNodeInfo(TreeNode node) {
if (node == null) {
return new NodeInfo(true, 0);
}
// 获取左子树信息
NodeInfo left = getNodeInfo(node.left);
// 获取右子树信息
NodeInfo right = getNodeInfo(node.right);
// 如果左右子树都平衡且高度差为 1 则我也平衡
boolean isBalanced = left.isBalanced && right.isBalanced && Math.abs(left.high - right.high) <= 1;
// 我的高度为左右子树最大高度 +1
int high = Math.max(left.high, right.high) + 1;
return new NodeInfo(isBalanced, high);
}
}
可以直接到 leetcode 验证 平衡二叉树
感受到二叉树的递归套路的魅力了吗?关键点在于:
- 思考 当前 节点 与 左右子节点的关系 (一般的我们可以以 以 与当前节点有关 和 与当前节点无关 来进行分类讨论 )
- 向左右子节点获取什么信息能够计算出我的信息
- 整合信息,定义结构
递归套路 2 计算给定树结构中二叉搜索子树的最大键和值
首先定义二叉搜索数 : 对于树中任意一个节点,其左树都小于该节点,右树都大于该节点
需要向左右节点要的信息:
- 树的最大值
- 树的最小值
- 是否是二叉搜索树
- 当前树的键和值
- 二叉搜索子树的最大键和值
在递归中就需要讨论最终结果是否与当前节点有关了,直接看代码
package algorithmic.base.tree;
import javax.xml.soap.Node;
/**
* @program: algorithmic-total-solution
* @description: 二叉搜索子树最大键和值 https://leetcode.cn/problems/maximum-sum-bst-in-binary-tree/
* @author: wangzibin
* @create: 2023-01-11
**/
public class MaxSumBST {
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public static class NodeInfo {
// 当前节点子树最大值
private int max;
private int min;
private boolean isBst;
private int bstSum;
private int bstMaxSum;
@Override
public String toString() {
return "NodeInfo{" +
"max=" + max +
", min=" + min +
", isBst=" + isBst +
", bstSum=" + bstSum +
", bstMaxSum=" + bstMaxSum +
'}';
}
}
public static NodeInfo getInfo(TreeNode node) {
if (node == null) {
NodeInfo empty = new NodeInfo();
empty.isBst = true;
empty.min = Integer.MAX_VALUE;
empty.max = Integer.MIN_VALUE;
return empty;
}
NodeInfo leftInfo = getInfo(node.left);
NodeInfo rightInfo = getInfo(node.right);
NodeInfo current = new NodeInfo();
current.max = max(node.val, leftInfo.max, rightInfo.max);
current.min = min(node.val, leftInfo.min, rightInfo.min);
// 判断是否与我有关, 当且仅当我也是二叉搜索树时最大值才与我有关,否则只需要比较子树值即可
if (leftInfo.isBst && rightInfo.isBst && leftInfo.max < node.val && rightInfo.min > node.val) {
// 左右子树都是搜索树,且 左子树最大值 小于 当前节点值 ,右子树最小值 大于 当前节点值,则可讨论与当前节点有关的情况
current.isBst = true;
current.bstSum = node.val + leftInfo.bstSum + rightInfo.bstSum;
current.bstMaxSum = max(current.bstSum, leftInfo.bstMaxSum, rightInfo.bstMaxSum);
} else {
current.isBst = false;
current.bstMaxSum = Math.max(leftInfo.bstMaxSum, rightInfo.bstMaxSum);
}
return current;
}
public static int max(int num1, int num2, int num3) {
return Math.max(Math.max(num1, num2), num3);
}
public static int min(int num1, int num2, int num3) {
return Math.min(Math.min(num1, num2), num3);
}
public static int maxSumBST(TreeNode root) {
if (root == null) {
return 0;
}
int bstMaxSum = getInfo(root).bstMaxSum;
return Math.max(bstMaxSum, 0);
}
public static void main(String[] args) {
TreeNode treeNode1 = new TreeNode(1);
treeNode1.left = null;
TreeNode treeNode10 = new TreeNode(10);
TreeNode treeNode5 = new TreeNode(-5);
TreeNode treeNode20 = new TreeNode(20);
treeNode1.right = treeNode10;
treeNode10.left = treeNode5;
treeNode10.right = treeNode20;
System.out.println(maxSumBST(treeNode1));
}
}
验证正确性 1373. 二叉搜索子树的最大键值和