Stewart平台简介及应用场景

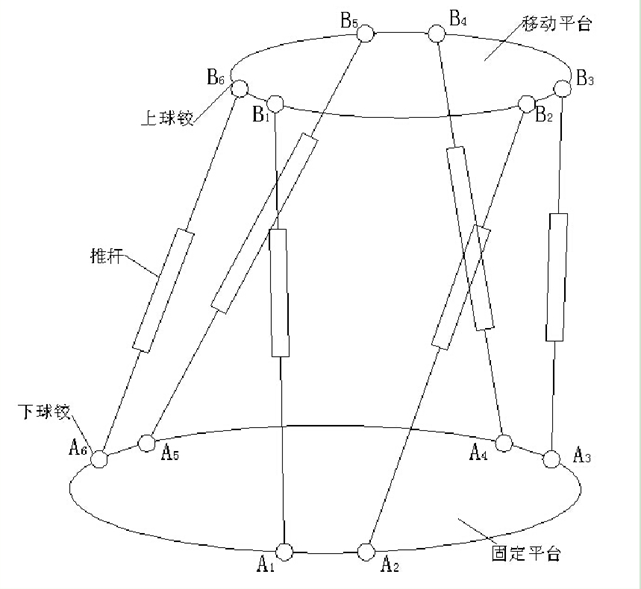
六自由度 Stewart 并联机器人结构简图如下图所示，主要有一个固定平台和一个移动平台以及六个可伸缩的推杆组成，通常情况下，固定平台与底座连接，移动平台在空间具有六个自由度，通过六个推杆的伸长或缩短可控制移动平台的位置和角度。实际应用中，根据不同的使用要求，伸缩杆可为电缸、液压缸或气缸。移动平台为末端执行器，伸缩杆为驱动器。

主要应用场合：

1. 飞行模拟器：上平台作为机舱, 用6个液压缸支撑和驱动, 可以使机舱获得任意需要的位置和姿态, 模拟飞机飞行状态, 用于训练飞行员。
   
2. 应用于飞船对接器。飞船对接器的下平台安装在输送物品的飞船上, 上平台作为对接环,由6个直线式驱动器, 上下平台中间都有通孔, 以便作为结合后的通道。潜艇救援中也应用类似的对接器。

3. 应用于设计虚拟轴机床。 一般采用悬挂式结构, 上平台悬挂固定, 下平台安装机床主轴单独驱动, 6 个支撑杆协调运动, 可以实现机床“ 6 轴联动” , 能够加工复杂的三维空间曲面。

4. 应用于设计6 维测力仪。 下平台固定, 6 个支撑杆用六个能测拉压力的传感器代替, 当上平台承受任意力螺旋(3个力和3 个力矩)时, 根据Stewart 平台机构静力学关系, 6 个支撑杆只承受拉压力, 所以很方便地测量六维力。 六维测力仪广泛地用于测量切削力和跑跳运动员的起动力。

Stewart平台自由度分析

每一根驱动杆由 2 个构件组成，因此，Stewart 平台的零件总数为 n = 2×6 + 1 + 1 = 14，根据 G-K 定律，Stewart 平台的自由度为：

由于每个驱动杆存在一个局部自由度。因此，Stewart 平台的实际自由度为6，即 3 个旋转自由度和 3 个移动自由度。此外，移动平台或固定平台上的六个球运动副可用虎克铰链代替，即，Stewart 平台也可以是 6-UPS 结构，且该结构不存在局部自由度。

Stewart平台运动学分析

结构描述：六自由度 Stewart 平台的机构分析简图，固定平台上六个球运动副分别为 A1, A2,…A6,移动平台上六个球运动副分别为B1,B2,…B6。在固定平台上建立坐标系 O-xyz，其原点 O 位于固定平台中心，x 轴穿过 A1 和 A2 的中点，z 轴竖直向上，y 轴由右手法则确定；在移动平台上建立坐标系 P-uvw，原点 P 位于移动平台的中心，u 轴、v 轴、w 轴分别于 x 轴、y 轴、z 轴平行且同向。 坐标建立见下图。

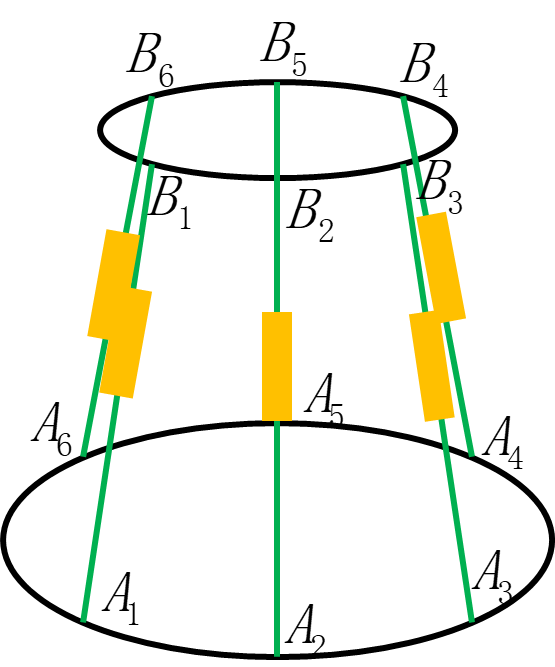
Stewart平台的坐标建立和动、静平台结构尺寸表示如下图所示：

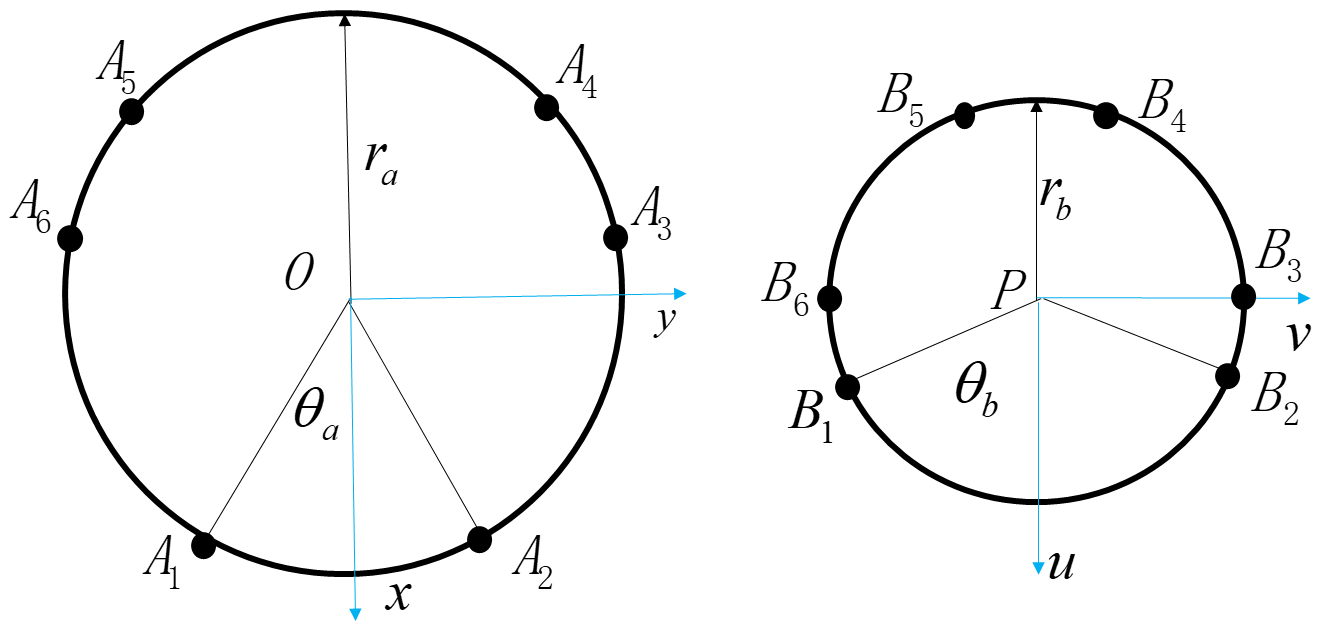
可以看到各平台上的 6 个球副 S 近似不等边对称六边形分布，动平台和定平台中各球铰位置可通过三个参数即可确定，这样就定义了平台的几何结构。
设动平台在空间中的广义坐标为：

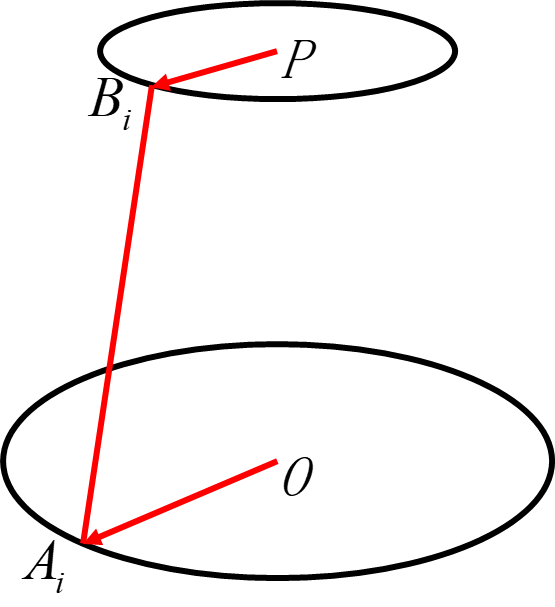
那么第i个伸缩杆的长度就为：

$$l_i=\sqrt{{\left(p+{}^O{R_P}^P{B}_i-{}^O{A}_i\right)}^T\left(p+{}^O{R_P}^P{B}_i-{}^O{A}_i\right)}$$

进一步简化可得：

$$l_i{e}_i=p+R{B}_i-A_i$$
那么杆的伸缩量就为：
$$\Delta l_i=l_i-l_0$$
其中：

详细课程讲解可见：机器人控制系列教程之Stewart平台简介和运动学分析

往期推荐