题目大意
已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵,你的任务是找到最大的非空(大小至少是
1
∗
1
1*1
1∗1)子矩阵。
比如,如下
4
∗
4
4*4
4∗4 子矩阵
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
的最大子矩阵是
9 2
-4 1
-1 8
这个子矩阵的大小是
15
15
15。
输入格式
输入一个 N ∗ N N*N N∗N ( 1 < = N < = 500 ) (1<=N<=500) (1<=N<=500)的整数矩阵,每个数的范围在 − 127 -127 −127~ 127 127 127 之间。
输出格式
输出最大子矩阵的大小。
输入样例
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
输出样例
15
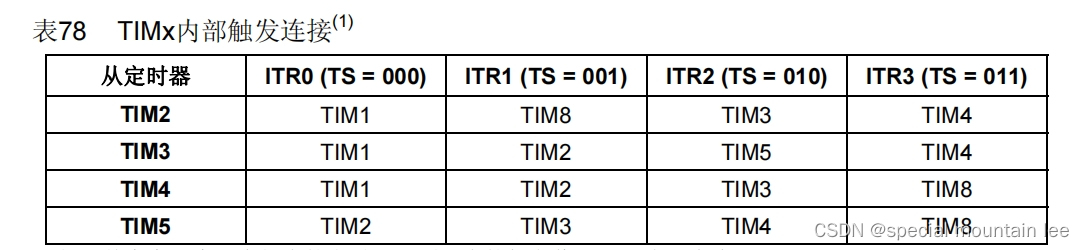
基本思路
我们的第一想法肯定是暴力枚举,但即便用二维前缀和优化依然是 O ( n 4 ) O(n^4) O(n4) ,明显是承受不了的。我们观察数据规模可以发现 O ( n 3 ) O(n^3) O(n3) 是可以承受的,因为每个 f o r for for 循环不一定都是 n n n ,那么怎么优化呢?
首先我们可以枚举枚子矩阵的宽度,即它有多少列。然后我们在将这个子矩阵中每一行的数加起来看成一个数。

此时我们得到了一个从上到下有
n
n
n 个数的数列(因为我们只枚举了宽度,长度即行数则默认为
n
n
n)。接下来就要确定行数了,现在问题就转化为在这
n
n
n 个数中选取一段和最大的连续子序列。 在这个图中就是
11
,
−
3
,
7
11, -3 , 7
11,−3,7,由此确定的子矩阵为
{
9
,
2
}
\{9,2\}
{9,2}
{
−
4
,
1
}
\{-4,1\}
{−4,1}
{
−
1
,
8
}
\{-1,8\}
{−1,8} 了。
还有一个问题需要注意,因为存在负值情况,所以 a n s ans ans 要赋一个极小值。
核心代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=510;
int n,s[N][N],ans=-1e9;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
cin>>s[i][j];
s[i][j]+=s[i][j-1];
}
for(int d=0;d<n;d++){//枚举宽度
for(int i=1;i+d<=n;i++){
int j=i+d,tmp=0;
for(int k=1;k<=n;k++){
tmp+=(s[k][j]-s[k][i-1]);//将此行的数看成一个数
ans=max(ans,tmp);
tmp=max(tmp,0);
}
}
}
cout<<ans;
// 2
// -4 -2
// -3 -1
//
// -1
return 0;
}