微积分，英文calculus，源自拉丁语，意为用于计数的小鹅卵石。

微积分都是关于变化的。这句话怎么理解呢？比如说，我们正在路上开着车，问此时此刻的车速是多少？我们可能会去看速度表显示多少。但是速度表上的速度是过去一段时间的平均速度：
$$平均速度=\frac{d}{\Delta t}$$

当这个Δt时间很短，得到的平均速度就会近似等于此时此该的瞬时速度，即

$$瞬时速度=\frac{\Delta d}{\Delta t}$$
当Δt无限小，趋于0时，这个等式就会有问题，除数为0。有没有什么数学工具可以求得一个可以无限逼近（近似）真实值的近似值呢？微积分就是目前为止可以用于做这件事的工具。它得到的值是一个无限逼近真实值的值，这就很有意义了，为什么呢？比如说10与10.00000000000000000000000000123这两个值的大小几乎可以认为是一样大的，因为无限逼近真实值时，相差的部分几乎可以忽略（因为小到几乎不存在，起不到任何影响，当哪一天这种影响不能忽略时，数学又应该要开始寻找另一种工具了）。

我们用一个例子来说明微积分的核心思想。假设计算物体从高处下落的距离公式为：
$$d=5t^2$$

d：下落距离，单位米
t：下落时间，单位秒
从上面的公式，我们可以在1秒后，物体下落了5米，那么此时的速度时多少？如果根据距离公式计算：5/1 = 5m/s，这个速度仍然是平均速度，因为用过去一段时间的距离除以这一段时间，只能得到这一段时间的平均速度，仍然无法得知每个时间点上的速度。但是我们用这个思想来做一些改变，我们在1秒往后再运动一段时间足够小的距离，用Δt表示这一小段时间。然后我们计算出这Δt时间的平均速度，用其来近似的表示t时间点上的瞬时速度。

(1+Δt)这一段时间的运动距离为：
$$d=5t^2=5\times (1+\Delta t{)}^2=5+10\Delta t+5(\Delta t{)}^2$$
那么Δt运行的距离为：
$$\Delta d=5\times (1+\Delta t{)}^2-5\times 1^2=5+10\Delta t+5(\Delta t{)}^2-5=10\Delta t+5(\Delta t{)}^2$$
那么Δt时间的平均速度为：
$$\frac{10\Delta t+5(\Delta t{)}^2}{\Delta t}=10+5\Delta t$$
当Δt时间无限小，趋向0时，那么10就是最后的结果了，我们就可以用10来近似表示1秒处的瞬时速度。这就是微积分了。

无限就是微积分的核心。这个工具就解决了前面除数为0的问题。
另外，数本身是没有什么意义的，数与数之间关系才是最重要的。比如说用正态分布的公式计算某个连续值的概率得到的数值具体是多少其实并不重要，重要的是它是比谁大或比谁小，这种对较出来的大或小的关系，已经足够了。

微分（Differential Calculus ）

上面计算得到某个时间点上的瞬时速度用的方法叫微分（Differential Calculus ） ，它把东西分成许许多多的微小的块，然后找出每一块的变化。微积分都是关于变化的，这个主题没有变到。上面的例子，就是将时间分成许多微小的块（大小为Δt），然后计算这一小块的变化。当我们用相同的方法处理一个代数方程时，我们就会得到一个东西叫导数。

在实际中，我们往往是用一个函数表达式去解决一类问题，当对这个函数进行类似前面的操作时，就会得到这个函数的导数。举个例子：我们有这样函数：
$$f(x)=x^3$$
我们来计算f(x+Δx)
$$f(x+\Delta x)=(x+\Delta x{)}^3=x^3+3x^2\Delta x+3x(\Delta x{)}^2+(\Delta x{)}^3$$
那么在Δx的变化是：
$$\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{x3+3x^2\Delta x+3x(\Delta x{)}^2+(\Delta x{)}^3-x^3}{\Delta x}=\frac{3x^2\Delta x+3x(\Delta x{)}^2+(\Delta x{)}^3}{\Delta x}=3x^2+3x\Delta x+(\Delta x{)}^2$$
化简后的结果就是
$$3x^2+3x\Delta x+(\Delta x{)}^2$$
当Δx无限小，趋向0时，
$$3x\Delta x+(\Delta x{)}^2$$
是可以忽略不计的，因此最后在x的变化就是
$$3x^2$$

刚刚我们这个过程就是一个求函数导数的过程。有了前面的铺垫我们再回来看看导数的概念。

导数（derivatives） ，derivatives的意思就是大量借鉴其他事物的事物，即基于另一个来源的东西。

刚刚我们说过微分就是将东西分成放多微小的东西，然后它的变化，这个变化就叫导数，专业的说法就是斜率（slope）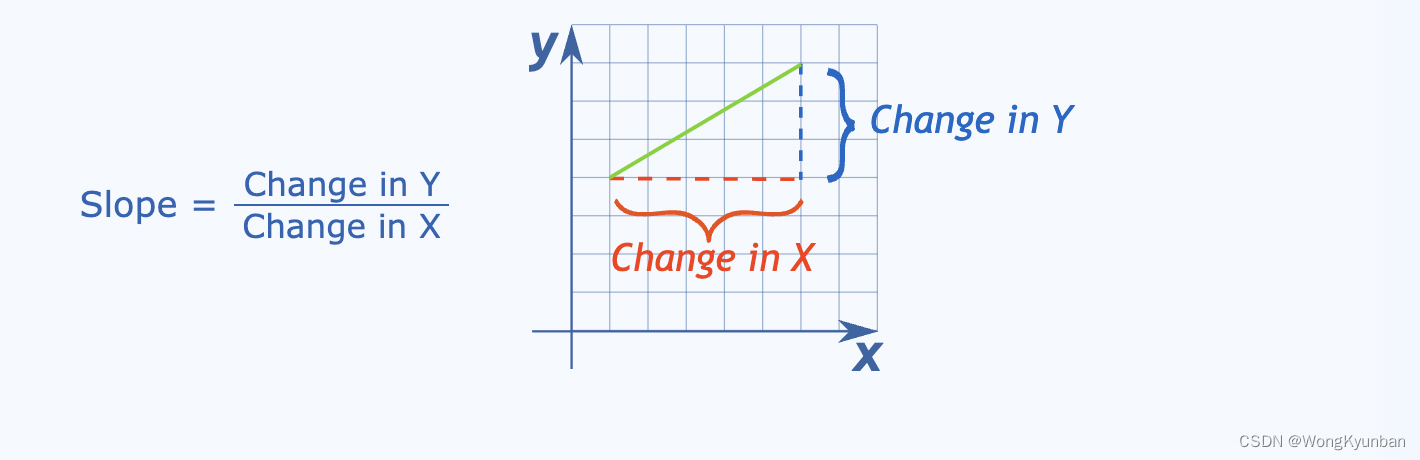
两点之间的平均斜率：

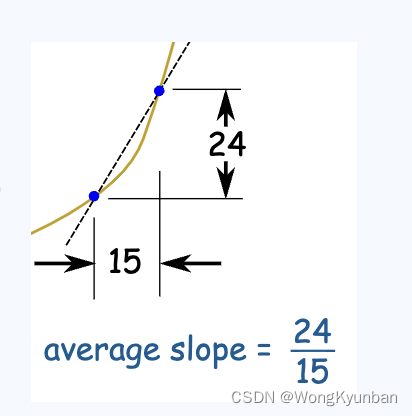
那么一点呢？下面讲到的过程 ，只是换另一种方式重复前面说的东西。

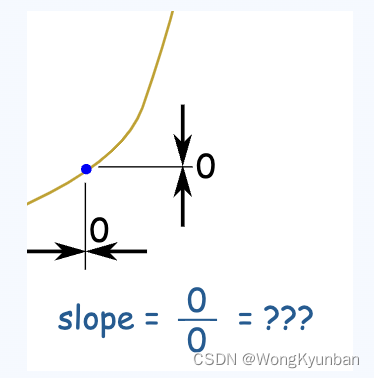
针对这种情况 ，我们要用极限的思想来思考，和它邻近的点构成一微小的一段，用这一段斜率去近似地表示这个点的斜率。如下图：

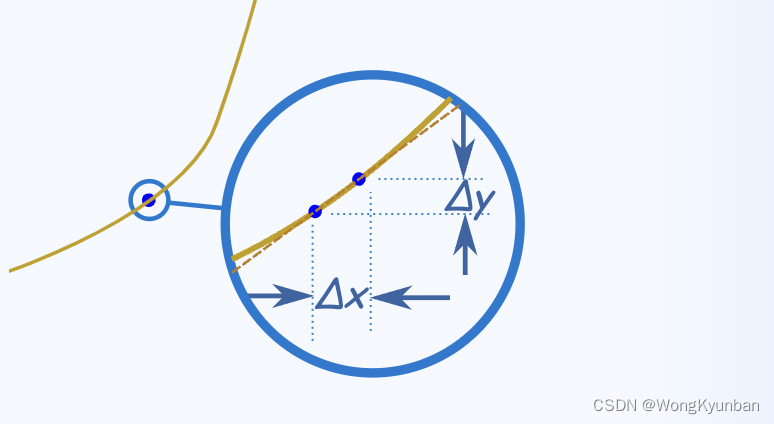
$$Slope=\frac{ChangeinY}{ChangeinX}=\frac{\Delta y}{\Delta x}$$

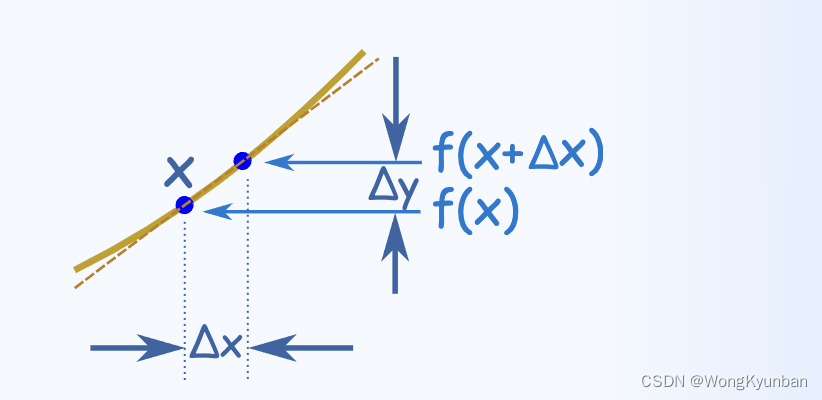
假设有一个y = f(x) ，那么它在某点上的斜率就会等于
$$Slope=\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

实际例子可以参考前面的内容：
$$f(x)=x^3$$

接下来我们看一下，这种数学的东西，如何用更数学的方式来表达，我们前都是用自然语言去描述导数，说它是来自某个函数的。

当我们要表达Δx趋向于 0 这个意思时，直接使用 dx。当我们要表达"某个函数的导数是…"这种表述时，用如下符号：
$$\frac{d}{dx}$$
例如：

$$\frac{d}{dx}{x}^3=3x^2$$
x 的三次方的函数的导数是 3 倍 x 平方。所以上这个式子，把 Δx趋向于 0 这个意思表达了，把函数的导数是什么也表达了。

表达函数的导数是什么，还有一种数学方式的表达：f’(x)。如f’(x) = 2x，表达f(x)函数的导数是 2x。

前面我们想表达Δx趋向于 0 时，即向 0 收缩，还可以表达成：
$$f^{\prime }(x)=\underset{x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
有时导数的表达还可以是如下形式：
$$\frac{dy}{dx}=\frac{f(x+dx)-f(x)}{dx}$$
不管表达形式如何，它们最终都只是想告诉你那个点的变化（斜率）是多少。

积分（Integral Calculus）

积分和微分是相反的动作。积分就是将许多微小的块连接（整合）在一起，看看总共有多少。积分就是这样一个通过将许多小块整合在一起找到整体的方法。积分常用于（但不限于）可用于面积、体积、中心点等等。比如计算下面这个面积：

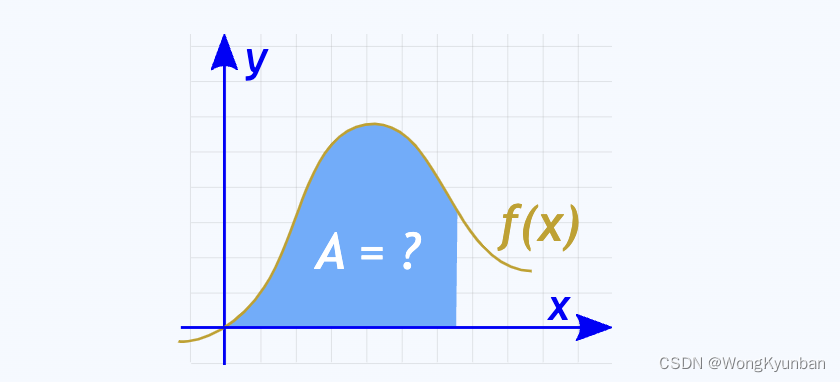
它不像正方形、矩形、直角三形、圆那样那么方便去计算它的面积。那么该如何求其面积呢？

我们可以在其中画许许多多的矩形：

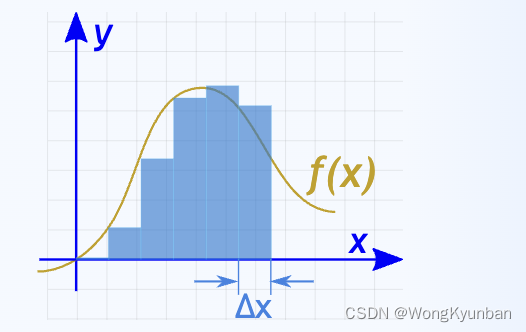
矩形的高就是f(x),宽就是Δx，将每个矩形的面积求出来再加到一起就是所要找的面积，但是这里的Δx有点大，导致空白的地方比较多，导致我们最后的结果误差比较大，所以我们再让Δx变得更小一些：

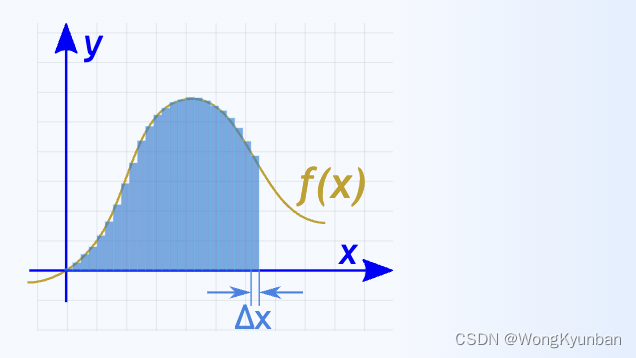
这样计算矩形的面积，最终得到的结果就比前一个的误差要小很多。我们利用极限的思想，使Δx趋向于 0，那么矩形就会无限逼近曲线（不可能完全贴合），得到的结果就会无限逼近真实的值。我们用dx表示矩形的宽的同时，也表示Δx（宽）趋向于 0这个意思。

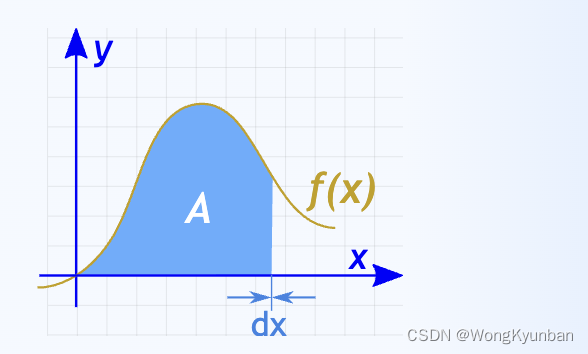
上面这个面积就是等于把这些微小的矩形面积累加在一起:
$$S=\sum _{i=1}^{n}f(x_i)\Delta x$$

那么我们就要累加许许多多这样的矩形，工作量是无限的！！！幸好，我们有一个捷径可以完成这项工作。

鉴于上面这个曲线函数较为复杂，因此我用下面这一个简单的函数来说明：
$$f(x)=2x$$

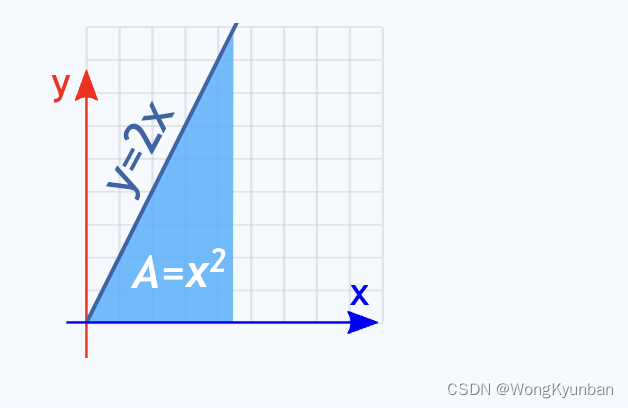
要计算上面围起来的面积，就相当于在计算一个直角三形的面积：
$$S=\frac{1}{2}(底)(高)=\frac{1}{2}xf(x)=\frac{1}{2}(x)(2x)=x^2$$

积分就是把许多微小的块累加起来达到积累的作用，从而求到面积、容量等，要用积分的办法去求这些值的原因是因为要求的对象都不是一些常见的且规则的形状（圆、矩形、直角三角形等等），所以常规的办法就显得局限，无效。那么在数学中如何用数学语言表达积分呢？
$$\int f(x)dx$$
上面第一个符号是拉长了的S，在英文中是sum（求和）的意思。上面这个表达就是说要对切片求和。切片就是我们分了许许多多的小矩形。切片的面积就是：底x高，即(dx)f(x)，dx就是底，同时表达宽Δx趋向0，就是宽取得无限小，高由f(x)求得。我们用积分的数学语言来表达一下求f(x) = 2x的面积：
$$\int f(x)dx=\int 2xdx=x^2$$
我们会很常听到人说，对某某函数积分，说得就是把这个函数在笛卡尔坐标（二维坐标）上围成的区域想成由许许多多宽趋于0（非常小的意思）的切片（小矩形），然后把它们累加起来的意思。所以上面我们就是对函数2x进行积分了。通过观察
$$函数2x与x^2的关系会发现2x是x^2的导数。$$
$$x^2是2x的其中一个原函数。x^2+c也是2x的原函数，c是一个常数项。$$
因为导数一定是来自某个函数（所以这个函数就叫原函数，这是相对导数函数来说的）。

因此，求积分的所谓捷径就是将被积函数（本例的被积函数是y=2x，被积函数，就是被用来做积分的函数），看成是某个函数的导数，然后找到这个导数的原函数，最后用原函数来求得积分（面积、容量等等）。

总结一下，对y=2x函数求积分的完整表达：
$$\int 2xdx=x^2+C$$
为什么要加上C呢？什么时候要加上C呢？我用另外一个例子来说明一下：

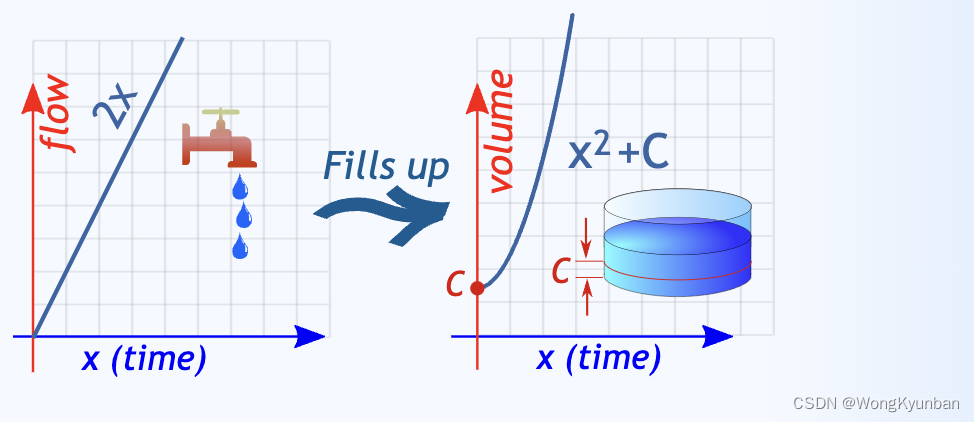
首先，我们在0时刻打开水龙头，往池子里流入水，水龙头水流速度是2x，随着时间的推移，水流速度逐步加快。

我们把每个时刻的流出来的水加起来就等于池子里的水，这明显是在做积分，对2x做积分。所以根据前面的学习，池子里水等于：
$$V=\int 2xdx=x^2+C$$
如果池子里原来就有C升的水，那么我们当然就要加上C。这样才能正确得到池子里现在有多少水。所以这里的常数C的值是要看情况来确定的。

通过这个例子，如果我们知道水的流速（本例是2x）可以推算出池子里的水的多少的函数（本例是x的平方），这个就是积分的过程，求导数的原函数，从切片整合到一个整体。反过来，如果我们知道池子水量的函数（本例是x的平方），也可以知道水龙头的流速（本例是2x），这就是微分的过程，求函数的导数的过程，从整体到切片。

上面说的积分都是不定积分（Indefinite Integral），Indefinite意思是不确定：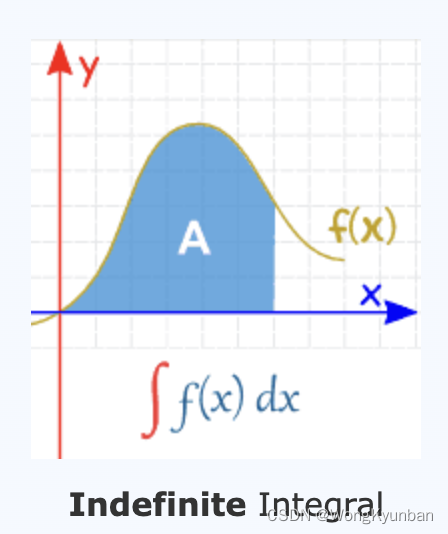
相对于不定积分，就有定积分（Definite Integral），Definite意思是确定、明确。所有定积分会明确求哪个区域的积分，它们用数学语言表达如下：

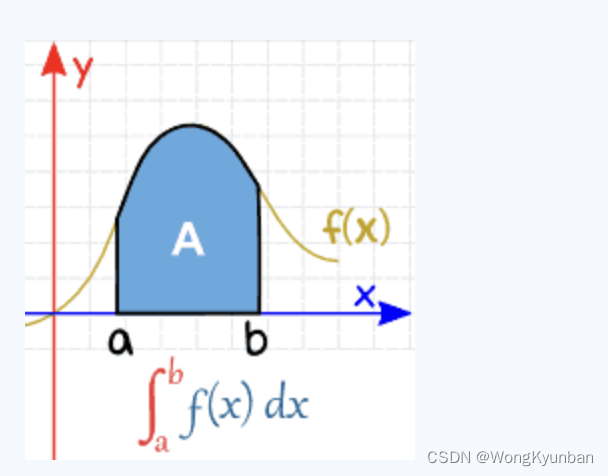
定积分有一个明确的开始和结束的边界值，如上图的[a,b]，分别放在S符号的下面和上面。表示从a到b的积分。我们仍然以y=2x这个函数来演示定积分：

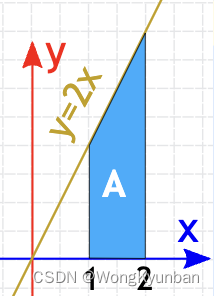
定积分的求解其实很简单的，先求a点的不定积分，再求b点的不定积分，然后相减，就能得到a到b的定积分。
由前面的学习我们可知y=2x的积分：
$$\int 2xdx=x^2+C$$
$$在1点的积分,x=1:\int 2xdx=x^2+C=1^2+C=1+C$$

$$在2点的积分,x=2:\int 2xdx=x^2+C=2^2+C=4+C$$

$$在[1,2]点的积分:2点的积分-1点的积分=（2^2+C）-（1^2+C）=3$$

因此：
$${\int }_1^{2}2xdx=3$$

标题结尾

单点的积分是0，根据定积分的计算先求上限的不定积分，再下限的不定积分，然后相减，在单点中，它的上下限是一样的，所有相减后得0 。

在概率中，连续量的概率是概率密度函数的积分。因此，概率是概率密度函数的积分。概率密度函数是概率的导函数。