目录
构建数据集
定义神经网络模型
定义超参、损失函数和优化器
超参
损失函数
优化器
训练与评估
构建数据集
首先从数据集 Dataset加载代码,构建数据集。
代码如下:
#引入了必要的库和模块,像 mindspore 以及相关的数据处理模块等等。
import mindspore
from mindspore import nn
from mindspore.dataset import vision, transforms
from mindspore.dataset import MnistDataset
# Download data from open datasets
#定义了一个下载函数,用于从特定的 url 下载 MNIST 数据集的压缩文件,并明确了保存路径。
from download import download
url = "https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/" \
"notebook/datasets/MNIST_Data.zip"
path = download(url, "./", kind="zip", replace=True)
#定义了一个叫做 datapipe 的函数,这个函数是用来处理数据集的。
def datapipe(path, batch_size):
#定义了一个名为 image_transforms 的列表
image_transforms = [
#将图像的像素值缩放到 0 到 1 的范围
vision.Rescale(1.0 / 255.0, 0),
#对图像进行标准化处理,使用给定的均值和标准差
vision.Normalize(mean=(0.1307,), std=(0.3081,)),
#改变图像的数据布局
vision.HWC2CHW()
]
#定义了一个名为 label_transform 的操作,用于将标签转换为 mindspore.int32 类型。
label_transform = transforms.TypeCast(mindspore.int32)
#通过 MnistDataset 类读取指定路径的数据集。
dataset = MnistDataset(path)
#使用 map 方法对数据集中的图像应用 image_transforms 中的变换操作,对标签应用 label_transform 操作。
dataset = dataset.map(image_transforms, 'image')
dataset = dataset.map(label_transform, 'label')
#使用 batch 方法将数据集按照指定的 batch_size 进行分批处理。
dataset = dataset.batch(batch_size)
#函数返回处理后的数据集。
return dataset 运行结果:

使用 datapipe 函数分别对训练集和测试集进行处理。为训练集和测试集指定了不同的路径,然而批大小均为 64 。处理结束后,将所得结果分别存放在 train_dataset 和 test_dataset 这两个变量当中,以便后续用于模型的训练与测试。
定义神经网络模型
从网络构建中加载代码,构建一个神经网络模型。
代码如下:
class Network(nn.Cell):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.dense_relu_sequential = nn.SequentialCell(
nn.Dense(28*28, 512),
nn.ReLU(),
nn.Dense(512, 512),
nn.ReLU(),
nn.Dense(512, 10)
)
def construct(self, x):
x = self.flatten(x)
logits = self.dense_relu_sequential(x)
return logits
model = Network() 分析:这段代码定义了一个名为 Network 的类,它继承自 nn.Cell 。
在 __init__ 方法(构造方法)中:
调用了父类的构造方法。
定义了一个 nn.Flatten 层用于展平输入数据。
定义了一个名为 dense_relu_sequential 的序列层,其中包含了三个全连接层(nn.Dense)和两个 ReLU 激活函数层。
在 construct 方法(前向传播方法)中,首先使用 flatten 层对输入 x 进行展平操作,然后将展平后的结果传入 dense_relu_sequential 序列层得到预测结果 logits 并返回。
最后,创建了一个 Network 类的实例并将其赋值给 model 变量。
定义超参、损失函数和优化器
超参
超参是可调节的参数,能掌控模型训练优化的进程,不同值可能影响模型训练与收敛速度。现今,深度学习模型多采用批量随机梯度下降算法优化。
就优化来说,超参是影响模型性能收敛的关键。常见的训练超参有:
训练轮次(epoch):指训练中遍历数据集的次数。
批次大小(batch size):数据集分批训练,其每个批次数据的大小就是 batch size 。过小则耗时且梯度震荡,不利收敛;过大则梯度方向不变,易陷局部极小值。所以要选合适的 batch size ,以提升精度和实现全局收敛。
学习率(learning rate):偏小会使收敛变慢,偏大可能导致训练不收敛等问题。梯度下降法常用于模型误差的参数优化,通过多次迭代和最小化损失函数预估参数,学习率控制着迭代中的学习进程。
代码如下:
#训练轮次设置为 3 次。
epochs = 3
#批次大小设定为 64 。
batch_size = 64
#学习率设置为 0.01 (1e-2 表示 10 的 -2 次方,即 0.01 )
learning_rate = 1e-2 损失函数
损失函数(loss function)用于衡量模型的预测值(logits)与目标值(targets)之间的偏差。在训练模型之初,随机初始化的神经网络模型往往会给出错误的预测结果。损失函数会评判预测结果和目标值的差异程度,模型训练的目的就是减小损失函数所计算出的误差。
常见的损失函数有用于回归任务的 nn.MSELoss(均方误差)和用于分类的 nn.NLLLoss(负对数似然)等。nn.CrossEntropyLoss 融合了 nn.LogSoftmax 和 nn.NLLLoss,能够对 logits 进行标准化并计算预测误差。
代码如下:
loss_fn = nn.CrossEntropyLoss() 分析:定义了一个损失函数变量 loss_fn ,并将其赋值为 nn.CrossEntropyLoss() ,即使用了 PyTorch 库中用于计算交叉熵损失的函数。在后续的模型训练中,会使用这个定义好的损失函数来计算模型预测结果与真实标签之间的误差。
优化器
模型优化(Optimization)是于每个训练步骤中调整模型参数以降低模型误差的过程。MindSpore 提供多种优化算法的实现,称为优化器(Optimizer)。优化器内部界定了模型的参数优化流程(即梯度如何更新至模型参数),所有优化逻辑皆封装于优化器对象内。在此,我们运用 SGD(Stochastic Gradient Descent)优化器。
我们借助 model.trainable_params()方法获取模型的可训练参数,并输入学习率超参来初始化优化器。
代码如下:
optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate) 分析:定义了一个优化器变量 optimizer ,使用了 PyTorch 中的随机梯度下降(Stochastic Gradient Descent,简称 SGD)优化器。它通过 model.trainable_params() 方法获取模型中可训练的参数,并将学习率设置为 learning_rate 这个变量所指定的值来初始化优化器。
训练与评估
第一步:定义了模型训练的相关函数和训练循环的逻辑。包括前向传播计算损失、获取梯度、单步训练以及整个训练过程的循环,并定期打印损失信息。
代码如下:
# 定义前向传播函数
def forward_fn(data, label):
# 模型对输入数据进行预测得到预测值 logits
logits = model(data)
# 根据预测值和真实标签计算损失
loss = loss_fn(logits, label)
# 返回损失和预测值
return loss, logits
# 获取梯度计算函数
grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=True)
# 定义单步训练的函数
def train_step(data, label):
# 调用梯度计算函数,得到损失和辅助信息,并计算梯度
(loss, _), grads = grad_fn(data, label)
# 优化器根据梯度更新模型参数
optimizer(grads)
# 返回损失值
return loss
def train_loop(model, dataset):
# 获取数据集的大小
size = dataset.get_dataset_size()
# 设置模型为训练模式
model.set_train()
# 遍历数据集中的批次
for batch, (data, label) in enumerate(dataset.create_tuple_iterator()):
# 执行单步训练并获取损失值
loss = train_step(data, label)
# 每 100 个批次打印一次损失信息
if batch % 100 == 0:
loss, current = loss.asnumpy(), batch
print(f"loss: {loss:>7f} [{current:>3d}/{size:>3d}]") 第二步:定义了一个测试循环的函数,用于在给定的数据集上对模型进行测试评估。计算了测试数据的平均损失和准确率,并打印出测试结果。
代码如下:
def test_loop(model, dataset, loss_fn):
# 获取数据集中的批次数
num_batches = dataset.get_dataset_size()
# 设置模型为评估模式(非训练模式)
model.set_train(False)
# 初始化一些统计变量
total, test_loss, correct = 0, 0, 0
# 遍历数据集中的数据和标签
for data, label in dataset.create_tuple_iterator():
# 模型对输入数据进行预测
pred = model(data)
# 累计数据的数量
total += len(data)
# 累计损失值
test_loss += loss_fn(pred, label).asnumpy()
# 计算预测正确的数量
correct += (pred.argmax(1) == label).asnumpy().sum()
# 计算平均损失
test_loss /= num_batches
# 计算准确率
correct /= total
# 打印测试结果
print(f"Test: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n") 第三步:进行了模型的训练和测试。首先定义了损失函数和优化器,然后按照设定的轮次数进行训练和测试,每一轮都打印轮次信息,最后打印训练完成的提示。
代码如下:
loss_fn = nn.CrossEntropyLoss() # 定义交叉熵损失函数
optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate) # 定义随机梯度下降优化器,并传入模型的可训练参数和学习率
for t in range(epochs): # 进行多个训练轮次
print(f"Epoch {t+1}\n-------------------------------") # 打印当前轮次信息
train_loop(model, train_dataset) # 执行训练循环
test_loop(model, test_dataset, loss_fn) # 执行测试循环
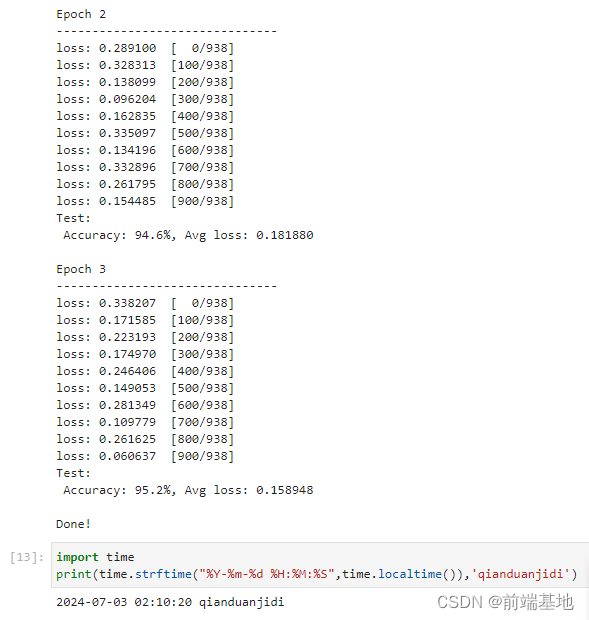
print("Done!") # 打印训练完成的提示 运行结果:
Epoch 1
-------------------------------
loss: 0.250805 [ 0/938]
loss: 0.130063 [100/938]
loss: 0.074891 [200/938]
loss: 0.330714 [300/938]
loss: 0.298072 [400/938]
loss: 0.177415 [500/938]
loss: 0.469457 [600/938]
loss: 0.380078 [700/938]
loss: 0.225529 [800/938]
loss: 0.200035 [900/938]
Test:
Accuracy: 93.9%, Avg loss: 0.207253
Epoch 2
-------------------------------
loss: 0.289100 [ 0/938]
loss: 0.328313 [100/938]
loss: 0.138099 [200/938]
loss: 0.096204 [300/938]
loss: 0.162835 [400/938]
loss: 0.335097 [500/938]
loss: 0.134196 [600/938]
loss: 0.332896 [700/938]
loss: 0.261795 [800/938]
loss: 0.154485 [900/938]
Test:
Accuracy: 94.6%, Avg loss: 0.181880
Epoch 3
-------------------------------
loss: 0.338207 [ 0/938]
loss: 0.171585 [100/938]
loss: 0.223193 [200/938]
loss: 0.174970 [300/938]
loss: 0.246406 [400/938]
loss: 0.149053 [500/938]
loss: 0.281349 [600/938]
loss: 0.109779 [700/938]
loss: 0.261625 [800/938]
loss: 0.060637 [900/938]
Test:
Accuracy: 95.2%, Avg loss: 0.158948
Done! 运行截图: