240703_昇思学习打卡-Day15-K近邻算法实现红酒聚类

news2024/7/6 19:09:48

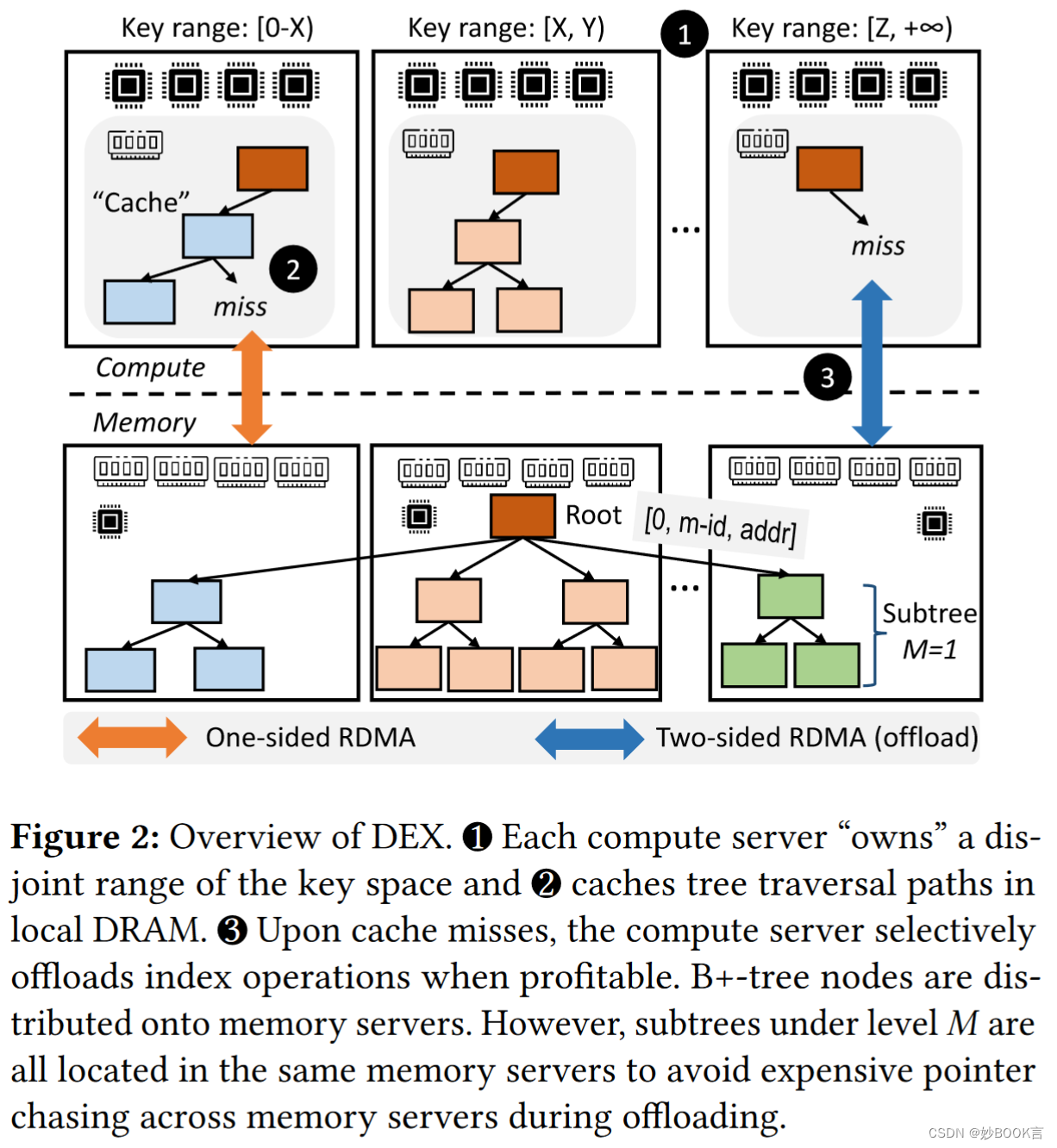
KNN(K近邻)算法实现红酒聚类

K近邻算法，是有监督学习中的分类算法，可以用于分类和回归，本篇主要讲解其在分类上的用途。

文章目录

KNN(K近邻)算法实现红酒聚类
- 算法原理
- 数据下载
- 数据读取与处理
- 模型构建--计算距离
- 模型预测

算法原理

KNN算法虽然是机器学习算法，但是他不学习，他的原理是把所有的训练集都存储下来，在测试的时候把测试集放到原图里面，根据测试点和训练集的距离判定属于的类别。如下图示例，假设我们现在有两个类别，分别是A和B，用三角和圆圈（不太圆见谅）表示，我们把这两种类别都画在坐标系中。此时载入一个未知类别方框，我们的KNN算法就开始了。

110098762832b5a36dc6b017825df1d

首先我们要指定一个K值，K值就是距离值，比如我们先指定K=2，就可以在这个位置类别周围画一个圆（可以理解为半径为2），如下图：

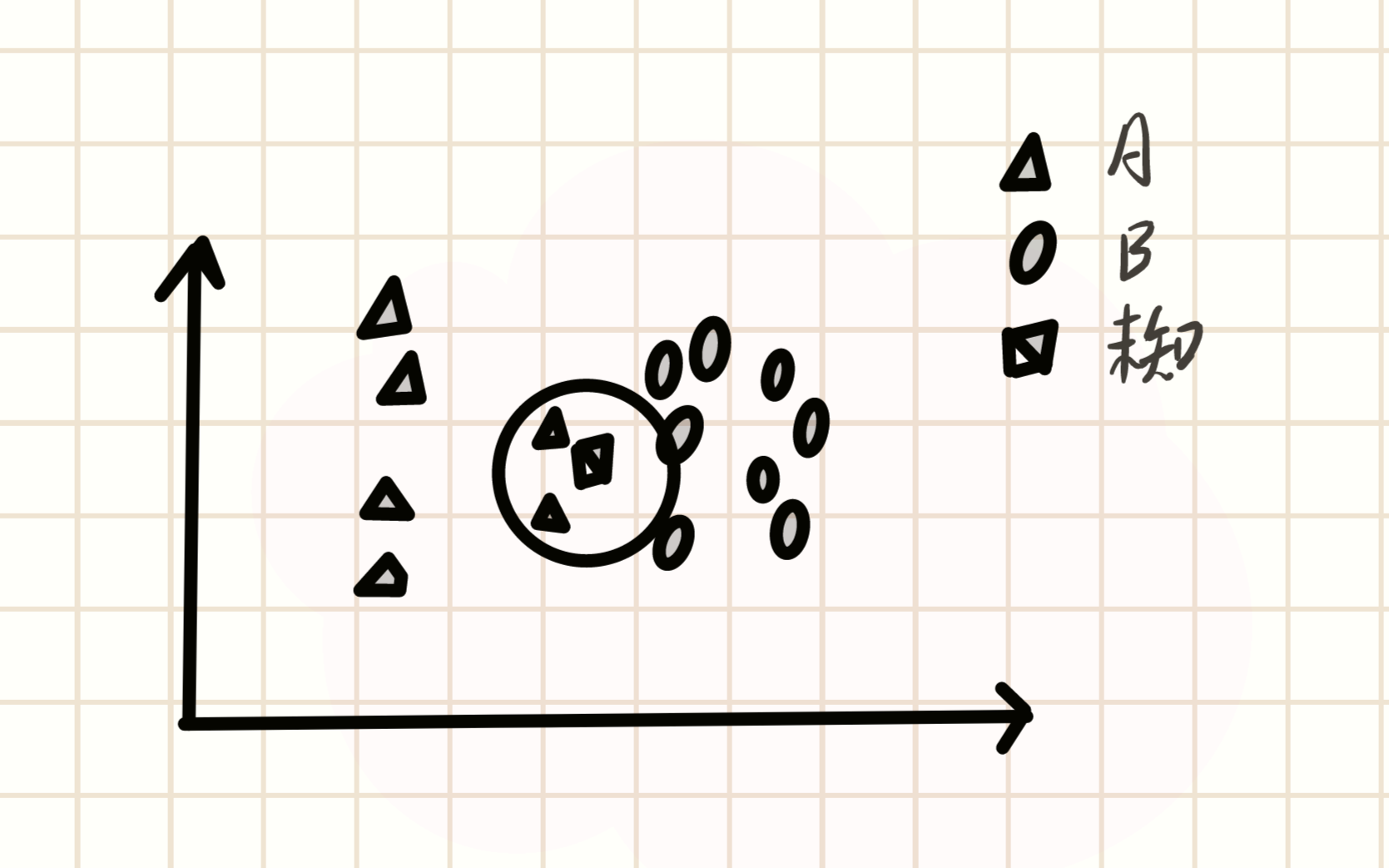
36b42e26031f9e5e878ea7b6e1a1df2

此时我们这个圆框进去了两个A类别，根据算法原理，此时就会把这个未知类别判断为A类别。而如果我们扩大K值呢

6ac9ca29672e8c05d90f380e5101696

当我们把K值从2扩大到4时（小圆外面的大圆），可以看到，此时包进来了4个B类别值，A类别值仍然只有2个，此时就会判断为B类别。这个算法有一点划地盘的意思，画个圈，这圈里谁人多，你就跟谁走，是这意思。歪理原理就这么结束了，下面让我们看看正经的解释。

K近邻算法（K-Nearest-Neighbor, KNN）是一种用于分类和回归的非参数统计方法，最初由 Cover和Hart于1968年提出(Cover等人,1967)，是机器学习最基础的算法之一。它正是基于以上思想：要确定一个样本的类别，可以计算它与所有训练样本的距离，然后找出和该样本最接近的k个样本，统计出这些样本的类别并进行投票，票数最多的那个类就是分类的结果。KNN的三个基本要素：

K值，一个样本的分类是由K个邻居的“多数表决”确定的。K值越小，容易受噪声影响，反之，会使类别之间的界限变得模糊。
距离度量，反映了特征空间中两个样本间的相似度，距离越小，越相似。常用的有Lp距离（p=2时，即为欧式距离）、曼哈顿距离、海明距离等。
分类决策规则，通常是多数表决，或者基于距离加权的多数表决（权值与距离成反比）。

预测算法（分类）的流程如下：

（1）在训练样本集中找出距离待测样本x_test最近的k个样本，并保存至集合N中；

（2）统计集合N中每一类样本的个数𝐶𝑖,𝑖=1,2,3,…,𝑐𝐶𝑖,𝑖=1,2,3,…,𝑐；

（3）最终的分类结果为argmax𝐶𝑖𝐶𝑖 （最大的对应的𝐶𝑖𝐶𝑖）那个类。

在上述实现过程中，k的取值尤为重要。它可以根据问题和数据特点来确定。在具体实现时，可以考虑样本的权重，即每个样本有不同的投票权重，这种方法称为带权重的k近邻算法，它是一种变种的k近邻算法。

数据下载

我们使用Wine数据集进行展示，Wine数据集的官网：Wine Data Set，这个数据集是对同一地区三个不同品种的葡萄酒进行化学分析后记录的结果。数据集分析了三种葡萄酒中每种所含13种成分的量。这些13种属性是

Alcohol，酒精
Malic acid，苹果酸
Ash，灰
Alcalinity of ash，灰的碱度
Magnesium，镁
Total phenols，总酚
Flavanoids，类黄酮
Nonflavanoid phenols，非黄酮酚
Proanthocyanins，原花青素
Color intensity，色彩强度
Hue，色调
OD280/OD315 of diluted wines，稀释酒的OD280/OD315
Proline，脯氨酸

可以采用两种下载方式：

方式一，从Wine数据集官网下载wine.data文件。
方式二，从华为云OBS中下载wine.data文件。

此时我们默认已经安装了Mindspore环境，采用从华为云OBS中下载数据集

from download import download

# 下载红酒数据集
url = "https://ascend-professional-construction-dataset.obs.cn-north-4.myhuaweicloud.com:443/MachineLearning/wine.zip"  
path = download(url, "./", kind="zip", replace=True)

数据读取与处理

数据下载下来了，我们就进行读取和预处理呗。

%matplotlib inline
import os
import csv
import numpy as np
import matplotlib.pyplot as plt

import mindspore as ms
from mindspore import nn, ops

ms.set_context(device_target="CPU")

with open('wine.data') as csv_file:
    data = list(csv.reader(csv_file, delimiter=','))
print(data[56:62]+data[130:133])

执行完这几行代码后我们会打印出来部分数据进行查看，比如我这里打印出这样的数据

此时最开始的每个list最开始的第一个数都是1或2或3，这就是葡萄酒的三种类别，后面紧跟着的13个参数就是他的13种化学成分。

取三类样本（共178条），将数据集的13个属性作为自变量X，将数据集的3个类别作为因变量Y。此时X和Y的值可以自行打印查看

X = np.array([[float(x) for x in s[1:]] for s in data[:178]], np.float32)
Y = np.array([s[0] for s in data[:178]], np.int32)

取样本的某两个属性进行2维可视化，可以看到在某两个属性上样本的分布情况以及可分性。

attrs = ['Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
         'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
         'OD280/OD315 of diluted wines', 'Proline']
plt.figure(figsize=(10, 8))
for i in range(0, 4):
    plt.subplot(2, 2, i+1)
    # 选择的化学成分由循环轮数i决定
    a1, a2 = 2 * i, 2 * i + 1
    # 选择前59个类别为1的数据，化学成分选a1和a2类
    plt.scatter(X[:59, a1], X[:59, a2], label='1')
    plt.scatter(X[59:130, a1], X[59:130, a2], label='2')
    plt.scatter(X[130:, a1], X[130:, a2], label='3')
    plt.xlabel(attrs[a1])
    plt.ylabel(attrs[a2])
    plt.legend()
plt.show()

这里执行完了就可以看到四张打印出来的图，就体现了每一类葡萄酒其中两种化学成分的关系

将数据集按128:50划分为训练集（已知类别样本）和验证集（待验证样本）：

train_idx = np.random.choice(178, 128, replace=False)
test_idx = np.array(list(set(range(178)) - set(train_idx)))
X_train, Y_train = X[train_idx], Y[train_idx]
X_test, Y_test = X[test_idx], Y[test_idx]

模型构建–计算距离

利用MindSpore提供的tile, square, ReduceSum, sqrt, TopK等算子，通过矩阵运算的方式同时计算输入样本x和已明确分类的其他样本X_train的距离，并计算出top k近邻

class KnnNet(nn.Cell):
    def __init__(self, k):
        super(KnnNet, self).__init__()
        self.k = k

    def construct(self, x, X_train):
        #平铺输入x以匹配X_train中的样本数
        x_tile = ops.tile(x, (128, 1))
        square_diff = ops.square(x_tile - X_train)
        square_dist = ops.sum(square_diff, 1)
        dist = ops.sqrt(square_dist)
        #-dist表示值越大，样本就越接近
        values, indices = ops.topk(-dist, self.k)
        return indices

def knn(knn_net, x, X_train, Y_train):
    x, X_train = ms.Tensor(x), ms.Tensor(X_train)
    indices = knn_net(x, X_train)
    topk_cls = [0]*len(indices.asnumpy())
    for idx in indices.asnumpy():
        topk_cls[Y_train[idx]] += 1
    cls = np.argmax(topk_cls)
    return cls

模型预测

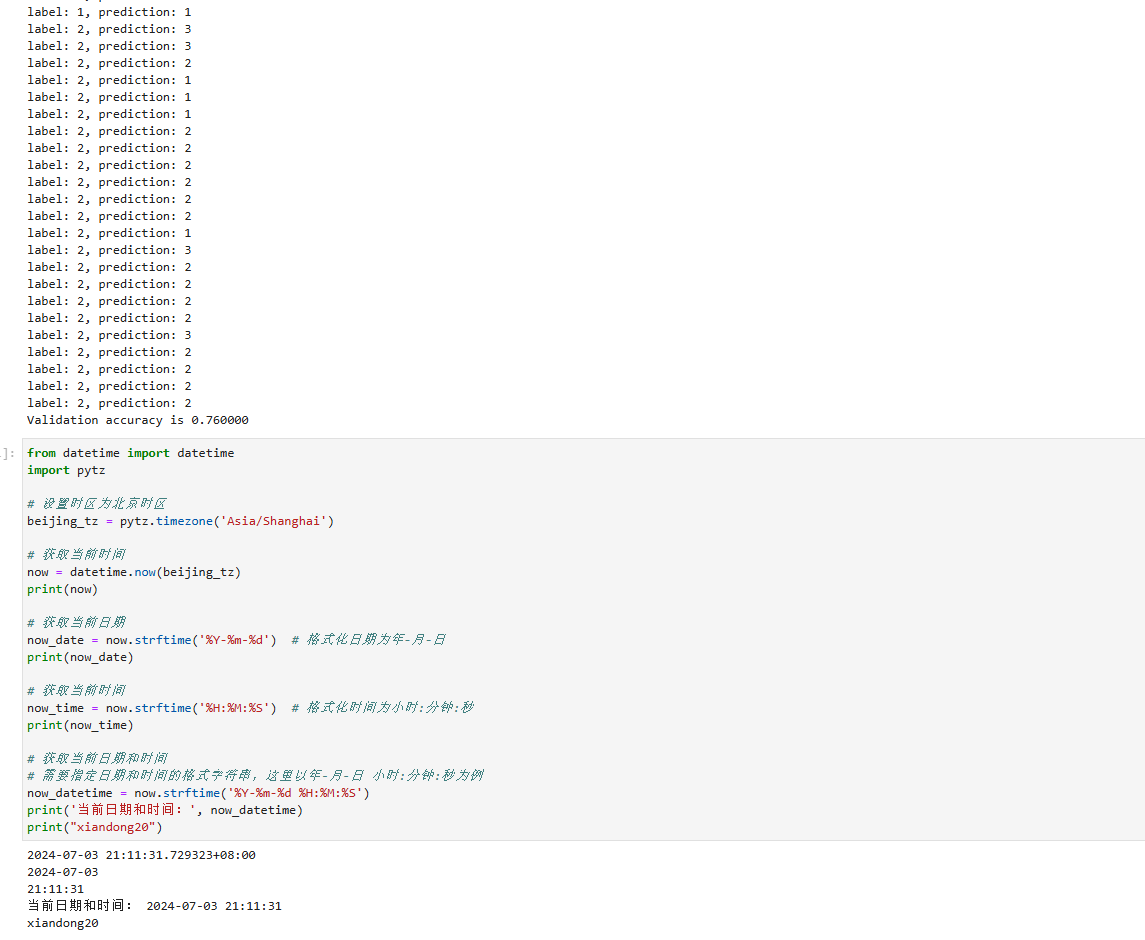
在验证集上验证KNN算法的有效性，取𝑘=5𝑘=5，验证精度接近80%，说明KNN算法在该3分类任务上有效，能根据酒的13种属性判断出酒的品种。

acc = 0
knn_net = KnnNet(5)
for x, y in zip(X_test, Y_test):
    pred = knn(knn_net, x, X_train, Y_train)
    acc += (pred == y)
    print('label: %d, prediction: %s' % (y, pred))
print('Validation accuracy is %f' % (acc/len(Y_test)))