一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

 我的写法：

代码结构

时间复杂度

空间复杂度

总结

我要更强

代码说明

时间复杂度

空间复杂度

哲学和编程思想

迭代与递归：

空间与时间的权衡：

抽象与具体化：

数据结构的选择：

内存管理：

算法优化：

举一反三

---

题目链接：https://leetcode.cn/problems/binary-tree-preorder-traversal/description/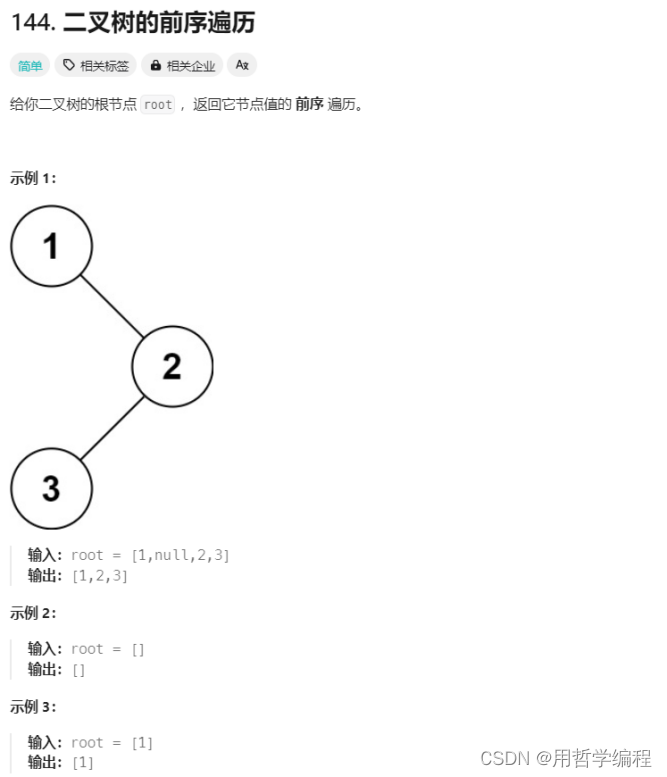

 我的写法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
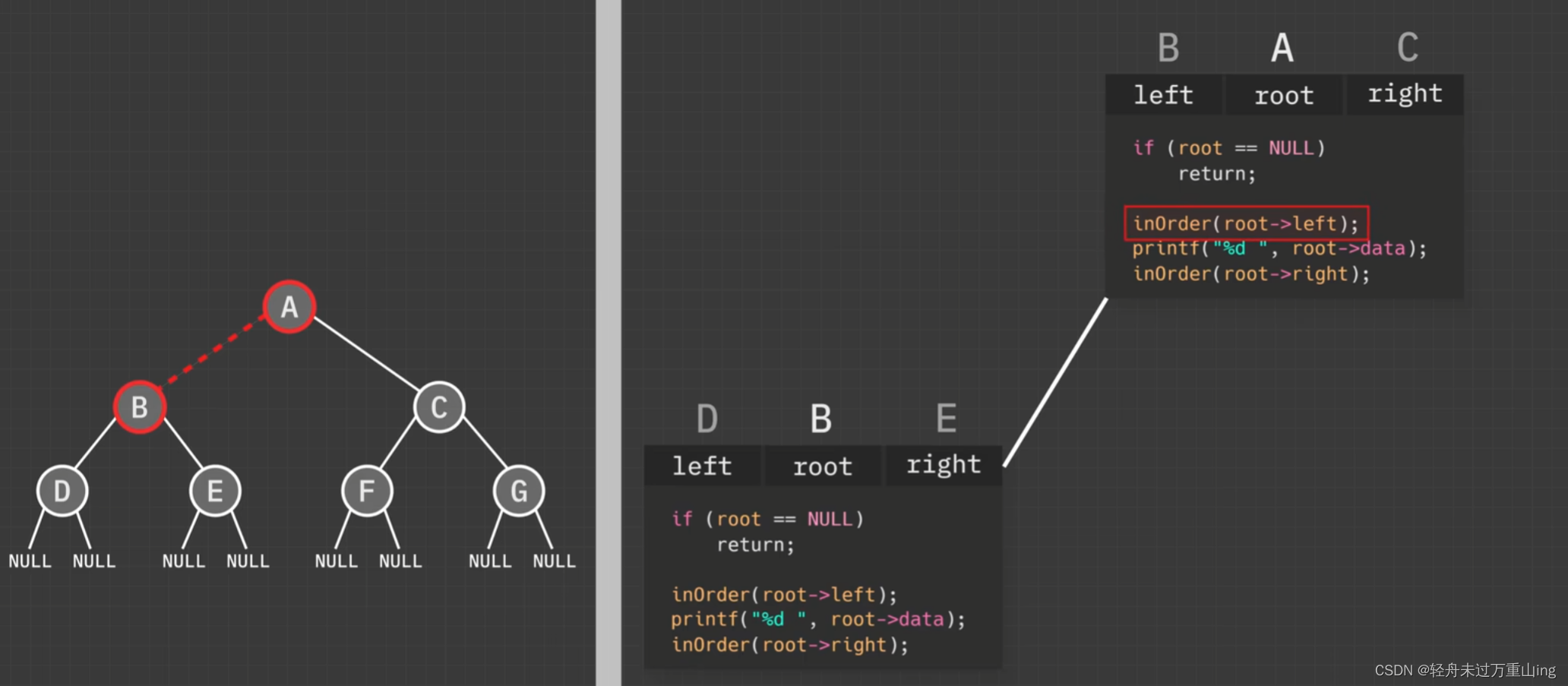
int TreeSize(struct TreeNode* root){
    return root == NULL ? 0 :1+TreeSize(root->left)+TreeSize(root->right);
}

void perorder(struct TreeNode* root,int* a,int* pi){
    if(root==NULL)
        return;
    
    a[(*pi)++]=root->val;
    perorder(root->left,a,pi);
    perorder(root->right,a,pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize=TreeSize(root);
    int* a=(int*)malloc(*returnSize*sizeof(int));

    int i=0;
    perorder(root,a,&i);

    return a;
}

这段代码实现了二叉树的前序遍历（Preorder Traversal），并返回一个包含遍历结果的动态数组。下面是对这段代码的专业点评：

代码结构

1. TreeSize 函数：
   • 该函数用于计算二叉树的节点数量。它通过递归地遍历左子树和右子树，并累加节点数来实现。如果根节点为空，则返回0；否则，返回1加上左子树和右子树的节点数。
2. perorder 函数：
   • 这是一个递归函数，用于执行前序遍历。前序遍历的顺序是：根节点 -> 左子树 -> 右子树。该函数将遍历到的节点值存储到数组 a 中，并通过引用传递的 pi 指针来更新数组索引。
3. preorderTraversal 函数：

• 这是主函数，负责分配返回数组的空间，调用 perorder 函数进行遍历，并返回遍历结果。它首先通过 TreeSize 函数确定返回数组的大小，然后分配相应大小的内存空间，并调用 perorder 函数填充数组。

时间复杂度

• TreeSize 函数：O(n)，其中 n 是树中的节点数。每个节点都被访问一次。
• perorder 函数：O(n)，同样地，每个节点都被访问一次。
• preorderTraversal 函数：O(n)，因为它调用了 perorder 函数，而 perorder 函数的时间复杂度是 O(n)。

空间复杂度

• TreeSize 函数：O(h)，其中 h 是树的高度。在最坏的情况下，递归调用的栈深度等于树的高度。
• perorder 函数：O(h)，同样地，递归调用的栈深度等于树的高度。
• preorderTraversal 函数：O(n)，因为需要分配一个大小为 n 的数组来存储遍历结果。此外，递归调用的栈空间也是 O(h)。

总结

这段代码有效地实现了二叉树的前序遍历，并且时间复杂度和空间复杂度都是合理的。注意，空间复杂度中的 O(h) 部分是由于递归调用栈的使用，这在树的高度较大时可能会成为一个问题。在实际应用中，需要考虑树的平衡性以及可能的最大高度。

---

我要更强

为了优化时间复杂度和空间复杂度，我们可以考虑使用迭代方法而不是递归来实现前序遍历。这样可以避免递归调用栈的空间开销，并且时间复杂度仍然是 O(n)，因为每个节点仍然只被访问一次。

下面是使用迭代方法实现的完整代码：

#include <stdlib.h>
#include <stdbool.h>

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    if (root == NULL) {
        *returnSize = 0;
        return NULL;
    }

    int* result = (int*)malloc(100 * sizeof(int)); // 假设最多100个节点，可根据实际情况调整
    struct TreeNode** stack = (struct TreeNode**)malloc(100 * sizeof(struct TreeNode*)); // 栈空间
    int top = -1; // 栈顶指针
    int index = 0; // 结果数组索引

    stack[++top] = root; // 根节点入栈

    while (top >= 0) {
        struct TreeNode* node = stack[top--]; // 出栈
        result[index++] = node->val; // 访问节点

        // 由于前序遍历是根-左-右，先右子树入栈，再左子树入栈
        if (node->right != NULL) {
            stack[++top] = node->right;
        }
        if (node->left != NULL) {
            stack[++top] = node->left;
        }
    }

    *returnSize = index; // 设置返回数组大小
    free(stack); // 释放栈空间
    return result;
}

代码说明

1. 栈的使用：我们使用一个栈来模拟递归调用的过程。在迭代方法中，我们手动管理这个栈。
2. 前序遍历的顺序：根节点首先被访问，然后是左子树，最后是右子树。因此，我们在栈中先压入右子树，然后是左子树，这样在出栈时，左子树会在右子树之前被访问。
3. 内存管理：我们动态分配了栈和结果数组的空间。在函数结束前，我们释放了栈的空间，但结果数组的空间由调用者负责释放。

时间复杂度

• O(n)：每个节点被访问一次。

空间复杂度

• O(h)：在最坏情况下，栈的大小等于树的高度。在最好情况下（平衡树），空间复杂度为 O(log n)。

这种方法在空间效率上优于递归方法，因为它避免了递归调用栈的空间开销。然而，它仍然需要一个栈来模拟递归过程，因此在最坏情况下的空间复杂度仍然是 O(h)。如果树非常不平衡，这可能会导致较高的空间使用。

---

哲学和编程思想

这些方法体现了以下哲学和编程思想：

1. 迭代与递归：

   • 递归是一种自我调用的方法，它依赖于调用栈来保存状态。递归通常使得代码更简洁、易于理解，但在处理大量数据时可能会导致栈溢出。
   • 迭代是一种循环结构，它通过显式地管理状态来避免递归的缺点。迭代通常更节省空间，因为它不需要额外的栈空间来保存中间状态。
   • 在上述代码中，我们使用了迭代方法来实现前序遍历，这体现了在空间效率和性能之间的权衡。

2. 空间与时间的权衡：

   • 在编程中，我们经常需要在空间复杂度和时间复杂度之间做出权衡。例如，使用额外的空间（如栈）来存储中间结果，可以减少时间复杂度。
   • 在迭代方法中，我们牺牲了一定的空间（栈空间）来减少递归调用栈的空间开销，从而优化了整体的空间复杂度。

3. 抽象与具体化：

   • 抽象是指忽略问题的某些细节，专注于核心概念。在二叉树遍历中，我们抽象出了遍历的顺序（根-左-右），而不关心具体的实现细节。
   • 具体化是指将抽象的概念转化为具体的实现。在迭代方法中，我们将抽象的遍历顺序具体化为栈的操作，通过入栈和出栈来实现遍历。

4. 数据结构的选择：

   • 选择合适的数据结构是编程中的一个重要决策。在二叉树遍历中，我们选择了栈作为辅助数据结构，因为它可以有效地存储和访问节点的顺序。
   • 栈的先进后出（LIFO）特性非常适合模拟递归调用的过程，使得我们可以在迭代中实现与递归相同的前序遍历顺序。

5. 内存管理：

   • 在C语言中，内存管理是一个重要的编程实践。我们手动分配和释放内存，以避免内存泄漏和悬挂指针。
   • 在代码中，我们动态分配了栈和结果数组的空间，并在不再需要时释放了栈的空间，这体现了良好的内存管理习惯。

6. 算法优化：

• 算法优化是提高程序效率的关键。在迭代方法中，我们通过优化栈的使用顺序（先右后左）来确保前序遍历的正确性，这是一种算法层面的优化。

这些哲学和编程思想是解决复杂问题的基石，它们帮助我们在设计和实现代码时做出明智的决策，以达到高效、可维护和可扩展的解决方案。

---

举一反三

根据上述哲学和编程思想，以下是一些技巧和策略，可以帮助在面对类似问题时举一反三：

1. 理解问题本质：
   • 在解决任何问题之前，首先要深入理解问题的本质。例如，在二叉树遍历问题中，理解前序遍历的定义（根-左-右）是至关重要的。
   • 技巧：将问题抽象为基本概念，然后从这些概念出发寻找解决方案。
2. 选择合适的数据结构：
   • 根据问题的特点选择合适的数据结构。例如，栈在处理需要逆序操作的问题时非常有用。
   • 技巧：熟悉各种数据结构的特性，并能够根据问题的需求灵活选择。
3. 迭代与递归的转换：
   • 学会将递归算法转换为迭代算法，或者反之。这种转换通常涉及到使用栈或队列来模拟递归调用栈。
   • 技巧：练习将递归算法重写为迭代算法，以提高对这两种方法的理解和应用能力。
4. 空间与时间的权衡：
   • 在设计算法时，考虑时间和空间的权衡。有时候，牺牲一些空间可以显著提高时间效率。
   • 技巧：评估不同解决方案的时间和空间复杂度，选择最合适的平衡点。
5. 内存管理：
   • 在需要手动管理内存的编程语言中，如C语言，注意内存的分配和释放。
   • 技巧：养成良好的内存管理习惯，确保在不再需要内存时及时释放。
6. 算法优化：
   • 不断寻找算法优化的可能性。例如，通过改变数据结构的使用顺序或方式来提高效率。
   • 技巧：分析算法的瓶颈，尝试不同的优化策略，如减少不必要的计算或改进数据访问模式。
7. 抽象与具体化：
   • 学会将复杂问题抽象为简单的模型，然后将这些模型具体化为可执行的代码。
   • 技巧：练习将问题分解为更小、更易于管理的部分，然后逐步构建解决方案。
8. 代码复用与模块化：
   • 在编写代码时，考虑代码的复用性和模块化。这有助于提高代码的可维护性和可扩展性。
   • 技巧：设计可重用的函数和类，将代码分解为独立的模块。
9. 测试与调试：

• 编写测试用例来验证代码的正确性，并使用调试工具来定位和修复错误。
• 技巧：编写全面的测试用例，使用调试工具逐步跟踪代码执行过程。

通过实践这些技巧和策略，将能够更好地理解和解决各种编程问题，提高你的编程能力和问题解决能力。记住，编程是一个不断学习和实践的过程，通过不断的练习和挑战，将能够举一反三，解决更复杂的问题。

---