目录
概述:
简单增量调制(∆M)原理:
编码器与解码器
简单△M的过载问题:
增量总和(∆-Σ)调制
数字压扩自适应增量调制:
不同编码调制方式的误码性能分析:
概述:
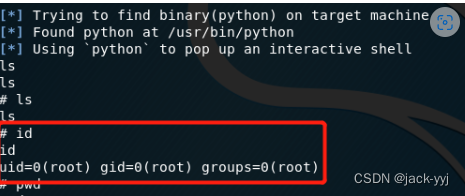
最简单的DPCM是增量调制,又称为ΔM。这时差值的量化级最简单,定为两级,也就是当差值为正时,输出“1”, 差值为负时,输出“0”,且每个差值只需1 bit。显然,为了减少量化失真必须增加取样率,使它远大于奈奎斯特取样率,即远大于2fm,其中fm为信源信号的上限频。译码时作相反变换,即规定一个增量值Δ,当收到“1” 时,在前一瞬间信号值上加上一个Δ值;收到“0”时,在前一瞬间信号值减去一个Δ值。
(1) 增量调制(∆M):一种信源编码方式;
(2) ∆M 调制的特点:每次抽样只输出1bit反映输入信号波形变换 的编码信号,简单可靠;
(3) ∆M 调制编码的基本思想:用一阶梯波逼近一个连续信号;
(4) ∆M 调制利用高采样率保证采样数据的相关性足够高,使得 使用简单的预测器时也可获得较小的预测误差;
(5) ∆M 调制的特点是接收处理时不需要码字的帧同步;
(6) ∆M 调制的主要应用:军用通信系统。
简单增量调制(∆M)原理:
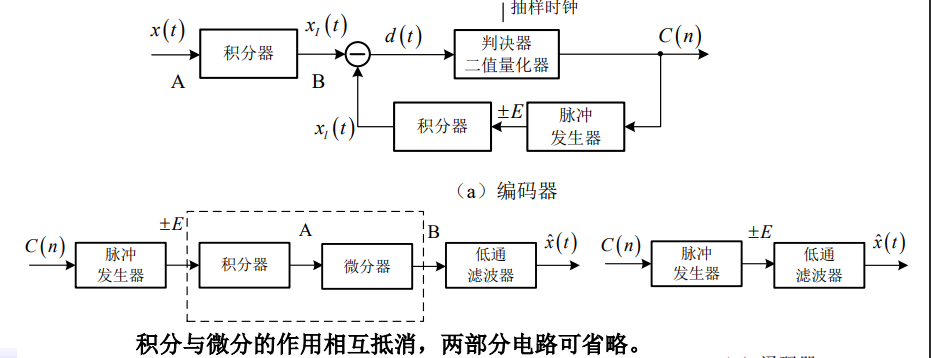
编码器与解码器
定义符号:
x(t):输入模拟信号;x(n): x(t)信号的抽样值;
xl (t):重建(本地译码)信号; xl (n):重建信号的样值;
d(t):差值信号;d(n):差值信号样值;
C(n):判决信号输出
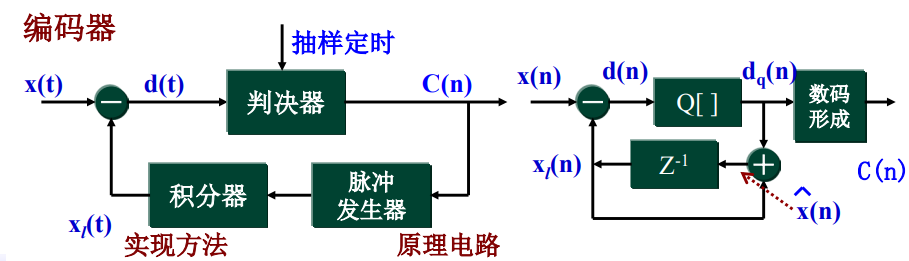
简单△M编码器的工作原理:

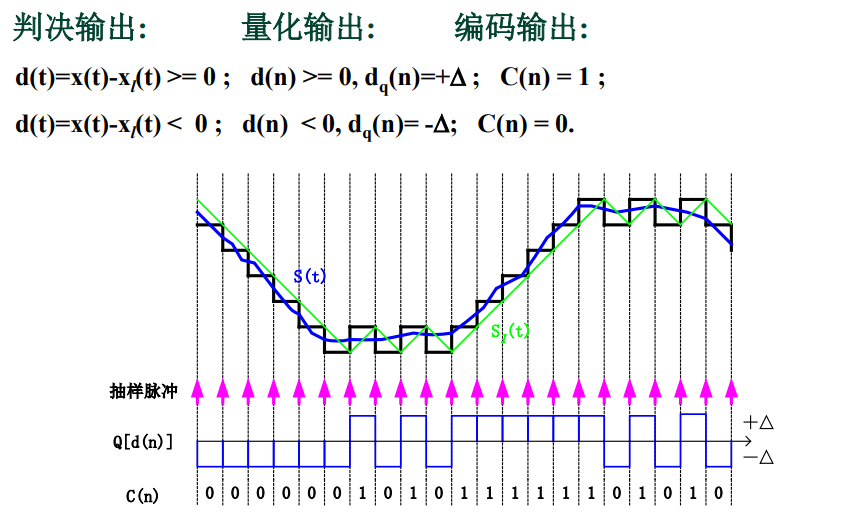
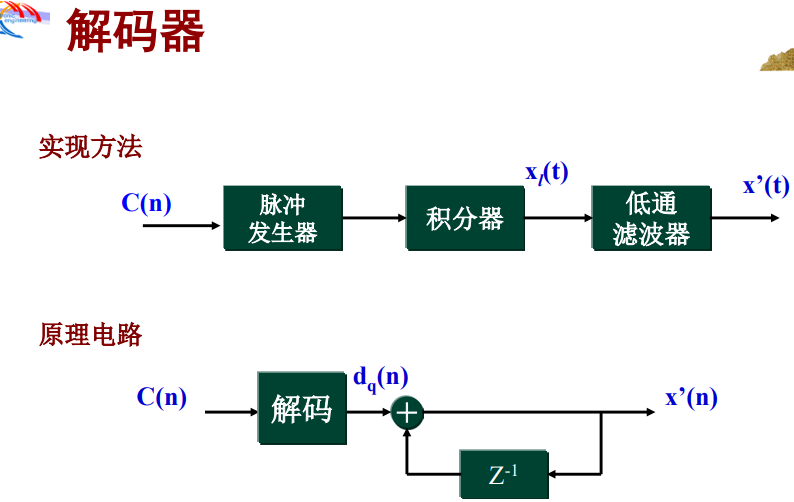
简单△M的过载问题:
重建信号的最大变化率:
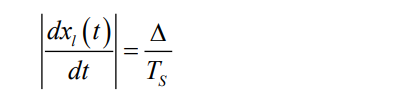
若输入信号变化率:

则重建信号可跟踪输入的变化。相应地接收端的重建信号可以恢复原信号的基本波形。
若输入信号的变化率:
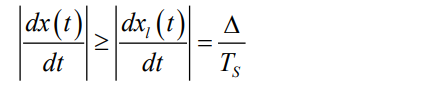
则重建信号无法跟踪输入的变化,相应地在接收端也将产生严重的失真。这就是所谓的△M的过载问题
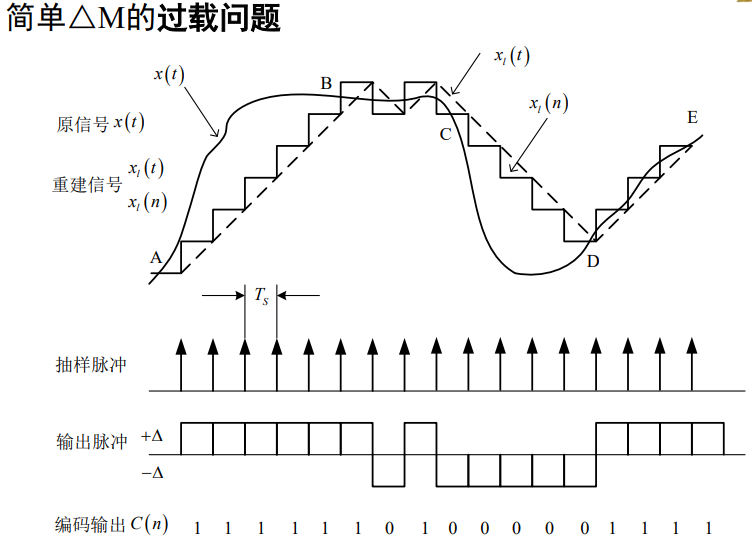
简单△M不发生过载的条件:
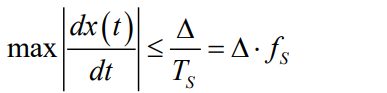

正弦波信号不过载和发生过载时的情形:

过载时的重建信号(译码信号)将会出现严重的失真
无过载失真的最大跟踪斜率:
![]()

增量总和(∆-Σ)调制
(1) 简单增量调制的缺陷
临界过载条件: fs∆ = Amax ω 与信号频率ω 有关;信号频率越高,越容易产生过载
(2) 增量总和(∆-Σ)∆M 基本原理
编码时,对信号作“积分”变换:A(ω) -> A(ω)/jω
临界过载条件: (A(ω)/jω)ω -> A(ω),
仅由信号幅度确定,与信号频率“无关”
解码时,对信号作相反的(“微分”)变换,恢复原信号
信号的幅度和频率是影响△M调制编码过载的主要因素。 △-∑调制改善简单△M调制的基本思想: 在编码前,先对信号做平滑的处理,抑制信号的突变成分,然后进行△M调制编码,由此可大大降低出现过载的可能性。
△-∑调制编码器和解码器:






对于△-∑调制编码器,临界不过载电压幅度与信号的频率f 无关, 而只取决于脉冲发生器产生脉冲的幅度E的大小
数字压扩自适应增量调制:
前面讨论的简单△调制和△-∑调制的量化阶距都是固定的,因此容易产生过载失真或无法兼顾量化噪声问题。
失真压控自适应△调制,借鉴了ADPCM的思想,使得量化阶距可根据输入信号的变化特性进行自动的调整。
数字压扩自适应△调制的原理如下图所示
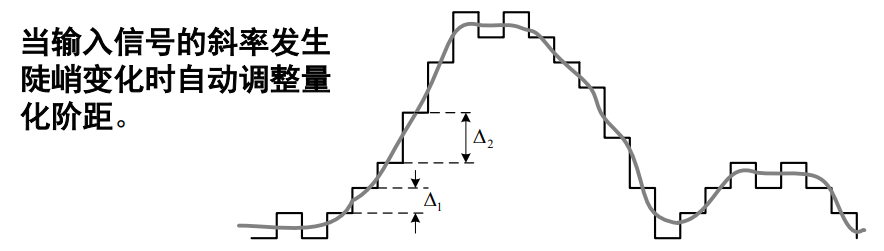
(1) 简单增量调制的缺陷
∆ 取值太小,容易产生过载失真;
∆ 取值太大,量化噪声增大
(2) 数字自适应压扩式 ∆M 基本原理
自动跟踪输入信号的变化,当连“0”或连“1”数目变化时,动态调节∆的大小

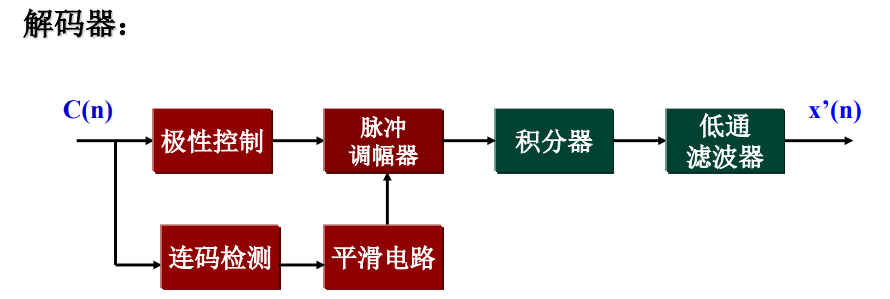
连码检测电路:检测连“0”或连“1”数目,获取自适应改变∆的信息
平滑(积分)电路:将检测输出的数字信号平滑后控制∆调幅器
极性控制:决定脉冲的极性 “0” 对应负脉冲; “1” 对应正脉冲
调幅器:动态确定∆的幅度大小
判决器与积分器:作用与普通的∆M中的相应部件功能相同
不同编码调制方式的误码性能分析:
结论:对比线性PCM编码,采用△M编码时,虽然其量化噪声的性能略低于线性PCM,但误码对系统劣化的影响将大大降低,从这个意义上说,△M编码具有更好的抗误码性能