1、递归

函数自己调用自己

递归的4个点：

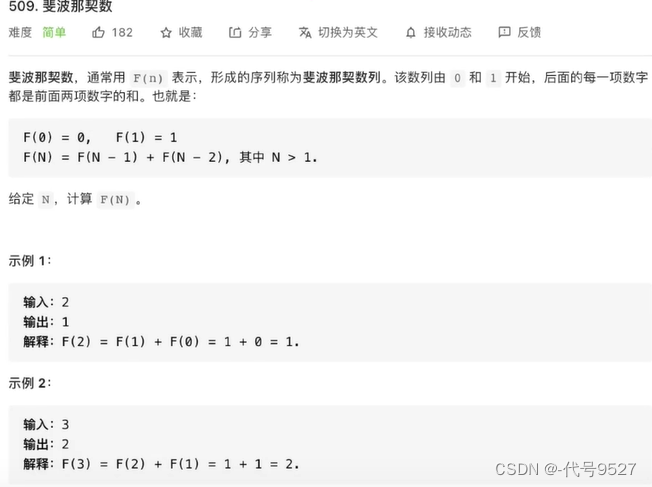
递归的例子：给一个数n，在斐波那契数列中，找到n对应的值

已知，f(0) = 0，f(1) = 1，求f(n)

一直拆f(n)，直到拆到f(0)或者f(1)时终止，这就是函数能return的条件（终止条件），拆解条件则是

f(n) = f(n-1) + f(n-2)

接收的参数自然是n，根据递归这四个点，写递归函数：

2、leetcode509：斐波那契数列

public class P509 {
    public static int recursion(int n) {
        if (n < 2) {
            return n == 0 ? 0 : 1;
        }
        return recursion(n - 1) + recursion(n - 2);
    }
}

3、leetcode206：反转链表

之前引入了虚拟节点，遍历，修改next指针，来实现了反转。其实倒过来应该想到栈，先放进去，再倒出来，就反转了。

这里用递归，也是栈的味道：将节点的next值往下传，直到末尾节点，return，如上面示例中的，到5时终止递归，下一层到节点4，将5的指向改为4，此时4、5互指，为了防止环形链表的出现，将4到5的next指向给断掉。

1->2->3->4<->5
1->2->3->4<-5

返回节点4时，将5指向4，即node.next.next = node

public class P206Two {
    /**
     * 每次执行reverseList方法的参数：
     * 第一次递归：head = 1，拆解后向下传入的是head.next，为2
     * 第二次递归：head等于上一层传入的值，head = 2，向下传入的参数为3
     * 第三次递归：head等于上一层传入的值，head = 3，向下传入的参数为4
     * 第四次递归：head等于上一层传入的值，head = 4，向下传入的参数为5
     * 第五次递归：head等于5，return，这层的reverseList方法执行结束
     * 开始回溯：
     * 到第四次递归：继续往下执行方法，head = 4，head.next.next 即 5.next，执行head，即把5指向4
     * 到第三次递归：继续往下执行方法，head = 3，head.next.next 即 4.next，执行head，即把4指向3
     */
    public static ListNode reverseList(ListNode head) {
        if (null == head || head.next == null) {
            return head;
        }
        ListNode newHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

4、leetcode344：反转字符串

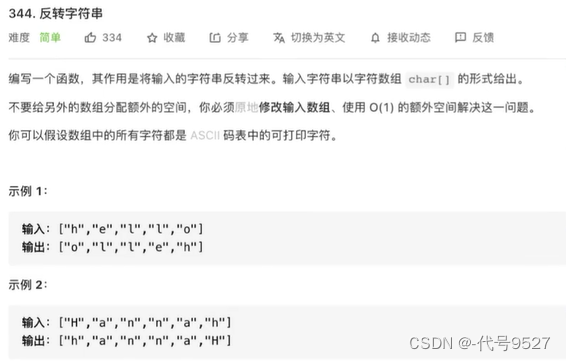
这个题用双指针最好，指针L在开始，指针r在末尾，两个指针对向移动，一直互换元素，直到 L >= r。如下，h和o互换，左右指针移动，e和l互换……

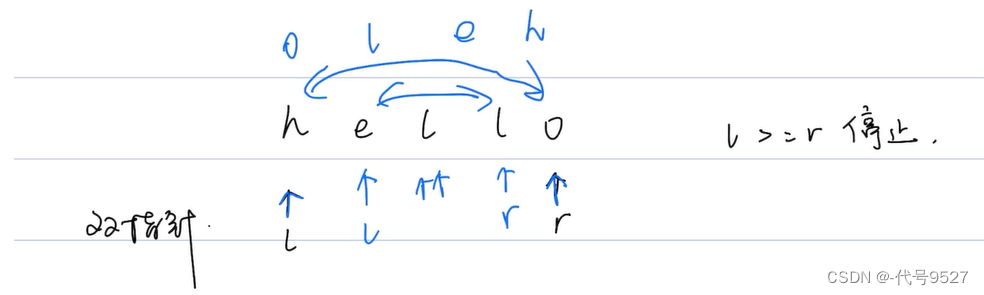
这里以双指针的思想为基础，硬套一层递归来实现：还是L和r两个指针，递归终止的条件是 L >= r，递归的拆解则是每次L指针+1，r指针-1，递归要传递的参数不再是一个，而是L和 r 两个，上一层递归结束，回溯回来时，交换L和r位置的元素

public class P344 {

    /**
     * 双指针解法
     */
    public static char[] reverseStringByTwoPoint(String s) {
        if (null == s || s.length() == 0){
            return null;
        }
        char[] charArray = s.toCharArray();
        int left = 0;
        int right = charArray.length - 1;
        while (left < right) {
            char temp;
            temp = charArray[left];
            charArray[left] = charArray[right];
            charArray[right] = temp;
            left++;
            right--;
        }
        return charArray;
    }

    /**
     * 双指针思想为基础，套一层栈的解法
     */

    public static char[] reverseStringByRecursion(String s) {
        if (null == s || s.length() == 0){
            return null;
        }
        char[] charArray = s.toCharArray();
        int left = 0;
        int right = charArray.length - 1;
        return recursion(charArray, left, right);
    }

    public static char[] recursion(char[] charArray, int left, int right){
        // 递归终止的条件
        if (left >= right) {
            return charArray;
        }
        // 递归的拆解
        char[] array = recursion(charArray, left + 1, right - 1);
        // 上一层递归结束，回溯回来时，交换元素顺序
        char temp = array[left];
        array[left] = array[right];
        array[right] = temp;
        return array;
    }


}

以hello为例，第一层递归，L = 0，R = 4，进入第二层递归，L = 1，R = 3，进入第三层递归，L= 2，R = 2，此时，触底，第三层递归函数执行return，结束，出栈。退到第二层递归，此时的L = 1， R = 3，交换这两个位置的元素，函数执行完成，出栈。退到第一层递归，此时L = 0，R = 4，交换这两个位置的元素，出栈。到此，三层递归都结束，方法执行结束。

递归时，盯清楚每一层递归时，参数等于多少，等递归回溯回来时，往下执行还要用。也别和传到下一层的参数混淆，因为用递归就会有参数拆解，每层递归函数里，值都不一样。如上，第一层递归，L = 0，R = 4，但其传入下一层递归的L和R分别为1和3