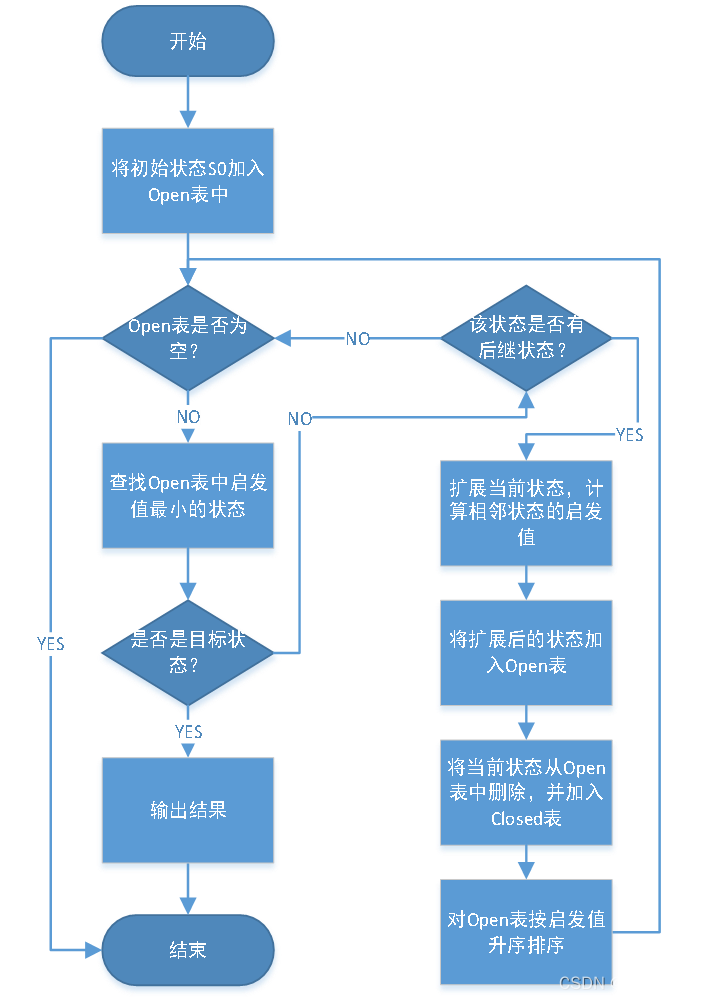
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

    

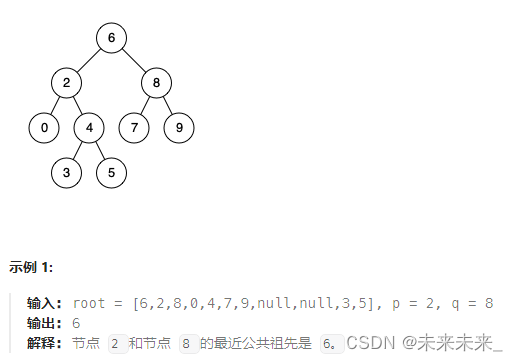
思路理解：

根据二叉搜索树的特性，递归时可以选择单边递归，

搜索一条边的写法：

if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;

重点在return上，满足条件进入左子树递归时，就只会一直沿着左边递归，有结果了就直接结束函数返回或者满足条件进入了向右方向的递归，总之，递归了一条线然后就返回。

搜索整个树写法：

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;

本题就是标准的搜索一条边的写法，遇到递归函数的返回值，如果不为空，立刻返回。

因为是二叉搜索树，是有序的，只存在三种情况：

1）q/p  < cur  < p/q  cur必是最近公共祖先，直接返回

2)   q,p <  cur  向左单边遍历

3)   q,p > cur  向右单边遍历

代码如下：

class Solution {
private:
    TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {
        if (cur == NULL) return cur;
                                                        // 中
        if (cur->val > p->val && cur->val > q->val) {   // 左
            TreeNode* left = traversal(cur->left, p, q);
            if (left != NULL) {
                return left;
            }
        }

        if (cur->val < p->val && cur->val < q->val) {   // 右
            TreeNode* right = traversal(cur->right, p, q);
            if (right != NULL) {
                return right;
            }
        }
        return cur;
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return traversal(root, p, q);
    }
};