目录
Debiasing Step
Denoising Step
Standard Error of the Regression Estimator
Debiasing Step
回想一下，最初由于混杂偏差，您的数据看起来是这样的、 随着信贷额度的增加，违约率呈下降趋势：
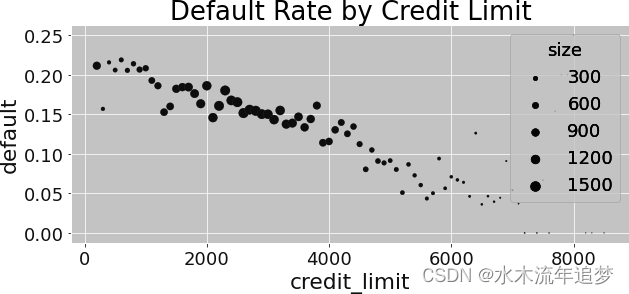
根据 FWL 定理，您可以通过拟合一个回归模型来预测混杂因素对信用额度的干预情况，从而对这一数据进行去伪存真。然后，您可以求出该模型的残差： 。这个残差可以看作是与去伪存真模型中使用的变量不相关的干预结果。这是因为，根据定义，残差与产生预测结果的变量是正交的。
这一过程将使残差以零为中心。您还可以选择将平均干预值
加回来：
这对于去偏是不必要的，但它将放在与原始
相同的范围内，这更适合于可视化的目的：
debiasing_model = smf.ols(
'credit_limit ~ wage + credit_score1 + credit_score2',
data=risk_data
).fit()
risk_data_deb = risk_data.assign(
# for visualization, avg(T) is added to the residuals
credit_limit_res=(debiasing_model.resid
+ risk_data["credit_limit"].mean())
)如果您现在运行一个简单的线性回归，将结果风险与去干预化或残差化的处理结果线性回归，您就已经得到了信用额度对风险的影响，同时控制了去干预化模型中使用的混杂因素。这里得到的 β1 参数估计值与之前运行完整模型得到的参数估计值完全相同，在完整模型中包含了干预和混杂因素：
model_w_deb_data = smf.ols('default ~ credit_limit_res',
data=risk_data_deb).fit()
model_w_deb_data.summary().tables[1]
但还是有区别的。看看 p 值。它比你之前得到的要高一些。这是因为你没有应用去噪步骤，而去噪步骤的作用是减少方差。尽管如此，考虑到所有的混杂因素都包含在去噪模型中，仅通过去噪步骤，您就可以得到信用额度对风险的因果影响的无偏估计值。您还可以通过绘制除权后的信用额度与违约率的对比图来直观地了解情况。你会发现，这种关系不再像数据有偏差时那样向下倾斜：
Denoising Step
去偏步骤对于估算出正确的因果效应至关重要，而去噪步骤虽然没有那么重要，但也是不错的选择。它不会改变干预效果估计值，但会减小其方差。在这一步中，您将对干预结果与非治疗的协变量进行回归。然后，您将得到结果的残差
同样，为了达到更好的可视化效果，您可以将平均默认设置率添加到去噪默认设置变量中：
denoising_model = smf.ols(
'default ~ wage + credit_score1 + credit_score2',
data=risk_data_deb
).fit()
risk_data_denoise = risk_data_deb.assign(
default_res=denoising_model.resid + risk_data_deb["default"].mean()
)Standard Error of the Regression Estimator
既然我们在讨论噪声，我想现在是了解如何计算回归标准误差的好时机。回归参数估计的 SE 由以下公式给出：
其中， 是回归模型的残差，DF 是模型的自由度（模型估计的参数数）。
model_se = smf.ols(
'default ~ wage + credit_score1 + credit_score2',
data=risk_data
).fit()
print("SE regression:", model_se.bse["wage"])
model_wage_aux = smf.ols(
'wage ~ credit_score1 + credit_score2',
data=risk_data
).fit()
# subtract the degrees of freedom - 4 model parameters - from N.
se_formula = (np.std(model_se.resid)
/(np.std(model_wage_aux.resid)*np.sqrt(len(risk_data)-4)))
print("SE formula: ", se_formula)这个公式很好，因为它能让你进一步直观地了解一般回归，特别是去噪步骤。首先，分子告诉你，你能预测的结果越好，残差就越小，因此估计值的方差就越小。这正是去噪步骤的目的所在。它还告诉你，如果干预方法能很好地解释结果，其参数估计的标准误差也会更小。
有趣的是，误差还与（残差化）干预处理的方差成反比。这也很直观。如果干预措施的方差很大，就更容易衡量其影响。
