# 租用游艇

## 题目描述

长江游艇俱乐部在长江上设置了 $n$ 个游艇出租站 $1,2,\cdots,n$。游客可在这些游艇出租站租用游艇，并在下游的任何一个游艇出租站归还游艇。游艇出租站 $i$ 到游艇出租站 $j$ 之间的租金为 $r(i,j)$（$1\le i\lt j\le n$）。试设计一个算法，计算出从游艇出租站 $1$ 到游艇出租站 $n$ 所需的最少租金。

## 输入格式

第一行中有一个正整数 $n$，表示有 $n$ 个游艇出租站。接下来的 $n-1$ 行是一个半矩阵 $r(i,j)$（$1\le i<j\le n$）。

## 输出格式

输出计算出的从游艇出租站 $1$ 到游艇出租站 $n$ 所需的最少租金。

## 样例 #1

### 样例输入 #1

```
3
5 15
7
```

### 样例输出 #1

```
12
```

## 提示

$n\le 200$，保证计算过程中任何时刻数值都不超过 $10^6$。

1.这道题看起来像是最短路径的问题，我觉得这道题考的更多的是动态规划。

2.这个题目意思说的比较笼统，于是我去看了题解，才明白题目是这样的意思：

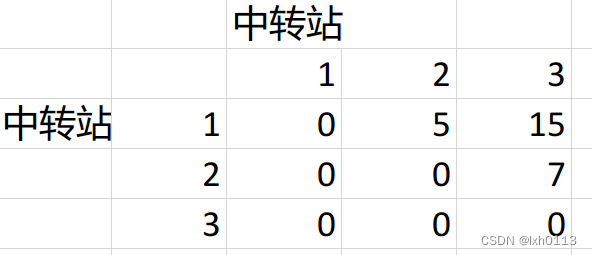
        1号可以到达的下一个中转站自然只有2号和3号，租金如下

        每个中转站只能到除它外的下个中转点。（这么说的话我觉得用floyd好像也是可以的）

 

 3.我们拿dp数组来记录，dp[  i  ]代表从1号点到  i  点的最少租金，我们每次都保证该点是最小值，那么除了1号点，其他的点都需要赋值为一个无穷大的数字（这里就拿2^31-1即可）。

4.在我们遍历每一点，它有俩种选择 

        第一个是它本身的值

        第二个是当前中转点 i 到  j  的租金值+dp[ i ]（这个代表的是1号点到  i  点取得的最少租金值）

于是代码实现即是：

外循坏代表从 中转点 i 开始  ，j  代表到达的中转点

最后输出dp[  n  ]即可。

C代码如下：

#include<stdio.h>
#define N 210
#define INF 2147483647
int a[N][N],n,dp[N];
int min(int a,int b)
{
	if(a>b) return b;
	return a;
}
int main()
{
	int i,j;
	scanf("%d",&n);
	for(i=1;i<n;i++)
	{
		dp[i+1]=INF;
		for(j=i+1;j<=n;j++)
			scanf("%d",&a[i][j]);
	}
	
	for(i=1;i<=n;i++)
	{
		for(j=i+1;j<=n;j++)
		{
			dp[j]=min(dp[j],dp[i]+a[i][j]);
		}
	}
	
	printf("%d ",dp[n]);
	return 0;
}

 C++代码如下：

#include<iostream>
#include<bits/stdc++.h>

using namespace std;

const int N=210;
const int INF=2147483647;

int a[N][N],n,dp[N];
int min(int a,int b)
{
	if(a>b) return b;
	return a;
}
int main()
{
	int i,j;
	cin >> n ;
	for(i=1;i<n;i++)
	{
		dp[i+1]=INF;
		for(j=i+1;j<=n;j++)
			cin >> a[i][j] ;
	}
	
	for(i=1;i<=n;i++)
	{
		for(j=i+1;j<=n;j++)
		{
			dp[j]=min(dp[j],dp[i]+a[i][j]);
		}
	}
	cout << dp[n] << endl;
	return 0;
}