目录
- 前言
- 一、hoare版本
- 1. 单排
- 2. 单排的代码实现
- 3. 综合排序的实现
- 4. 测试
- 二、挖坑法
- 1. 单排
- 2. 单排的代码实现
- 3. 综合排序的实现
- 4. 测试
- 三、前后指针法
- 1. 单排
- 2. 单排的代码实现
- 3. 综合排序的实现
- 4. 测试
- 四、快排的时间复杂度
- 五、快排的优化
- 1. 三数取中
- 2. 小区间优化
- 六、快排的非递归实现
前言
快速排序的效率是所有排序算法中比较高的一种排序算法了,其非常之重要,在校招中的考试也经常会遇到。我们今天重点学习的就是快速排序的相关内容,快速排序有三种版本,我们都必须熟练掌握。
一、hoare版本
1. 单排
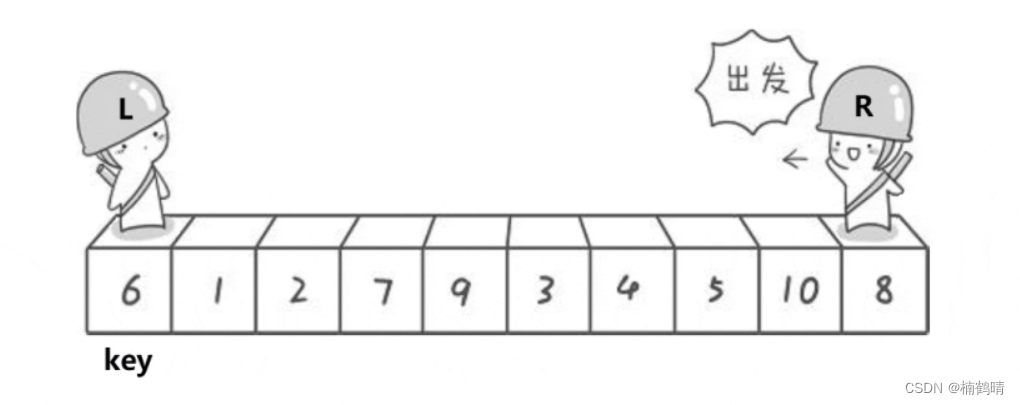
思想:一般情况下,首先选择左边第一个数字作为一个基准值,记为key,其对应的下标为
keyi。需要两个指针分别从左边第一个位置开始,另一个指针从右边最后一个位置开始,然后遍历整个数组,左边开始的指针称为left,右边开始的指针称为right,这里需要注意,遍历指向数组中的数据的指针就是数组的下标,也就是一个整数。left在遍历的过程中主要的任务就是找到比key大的数,right的任务就是找到比key小的数,然后再交换left和right指向的值,这个操作本质就是将比key小的数往前放,比key大的数往后放,最后实现keyi位置的左边所有值都比keyi位置的值小,keyi位置的右边所有值都比keyi位置的值大。继续遍历,重复上述过程,直到left和right相遇。最后将left和right相遇位置的值和keyi位置的值进行交换,这里需要注意一个点:我们定义的是keyi,也就是key对应的位置(下标),我们不能通过定义一个key去保存keyi对应位置的值,然后跟相遇位置进行交换,因为,这样定义的变量是一个局部变量,其改变不会影响数组中keyi位置的值。
- 注意事项:
- 如果是以最左边的值作为key,则一定要先让right先走,保证最后相遇位置的值比key小,然后和keyi位置的值进行交换,这样交换后刚好比keyi位置的值小的值放到keyi的左边。
- 如果是以最右边的值作为key,则一定要先让left先走,保证最后相遇位置的值比key大,然后和keyi位置的值进行交换,这样交换后刚好比keyi位置的值大的值放到keyi的右边。
- 关于相遇位置的值?
- 如果是以最左边的值作为key,则一定要先让right先走:相遇的情况有两种,第一种就是left去遇到right,此时的场景是right找到对应的数据之后停下来,换left进行找数据,但是left还没有找到对应的数据就遇到了right,此时因为是right停下来的,所以该位置的值显然是比keyi位置的值小的。第二种情况就是right去碰left,这种情况发生在left和right对应的值刚交换后,right继续走,但是没有找到比keyi位置的值小就遇到了left,此时需要注意left指向的值是刚刚和right指向的值进行交换的,所以此时left指向的值是比keyi位置的值小的。
- 如果是以最左边的值作为key,则一定要先让left先走:相遇的情况有两种,第一种就是right去遇到left,此时的情况是left找到了比keyi位置的值大了,停下来了,right没有找到比keyi位置的值小就遇到left了,显然相遇位置的值是比keyi大的。第二种情况就是left去遇到right,此时left和right的位置的值刚发生交换,此时left要去寻找下一个比keyi位置的值大的,但是此时没有找到就遇到了right,此时right位置指向的值是上一次left和right发生交换的结果,显然是比keyi指向的值大的。
2. 单排的代码实现
int PartSort(int* a, int left, int right)
{
assert(a);
int keyi = left;
while (left < right)
{
// 先让right走
while (left<right && a[right]>=a[keyi])
{
right--;
}
// 再让right走
while (left < right && a[left] <= a[keyi])
{
left++;
}
// left和right都找到了对应值,left找到了比keyi位置大的值,right找到了比keyi位置小的值
// 交换
Swap(&a[left], &a[right]);
}
// 当相遇时退出循环
Swap(&a[keyi], &a[left]);
return left;
}
- 注意事项: 上述的代码中有几个细节:
- 在内层循环中的while循环中一定要加上left<right这个条件,否则就会出现left或者right越界的情况。
- 内层循环的while循环中写的一定是
a[right]>=a[keyi]和a[left] <= a[keyi],一定不能写成a[right]>a[keyi]和a[left] < a[keyi],如果写成这样,当数据和keyi对应的值相等的时候,那么left和right都不会往下走,那么就会出现死循环。
3. 综合排序的实现
综合快速排序的实现需要利用分治算法思想,也就是需要对keyi的左右子区间进行递归使用单排,当所有的子区间都有序的时候,那么整个数据就是有序的
。
- 代码实现
// 快排
void QuickSort(int* a, int begin, int end)
{
assert(a);
if (begin >= end)
{
// 判断区间的有效性
// 如果区间中只有一个数,那么此时默认是有序的,不需要进行单排
// 如果区间不存在,同样不能进行单排
return;
}
// 区间有效
// 进行单排
int keyi = PartSort(a, begin, end);
// 将原数组区间[begin,end]分为[begin,keyi-1],keyi,[keyi+1,end]
// 递归单排左右子区间,使每一个子区间都有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
4. 测试
- 测试代码
void TestQuickSort()
{
int a[] = { 9,8,7,6,5,4,3,2,1 };// 逆序
int size = sizeof(a) / sizeof(int);
QuickSort(a, 0,size-1);
PrintArr(a, size);
}
int main()
{
TestQuickSort();
return 0;
}
- 测试结果

二、挖坑法
1. 单排

思想:首先将第一个位置的值l,l也就是eft指向的值保存为key,那么此时left位置就是一个坑,可以填充数据。同样,我们让right先走,当right找到了比key小的数,那么此时将找到的数放到坑位上,此时自己(right位置)形成一个坑位,接下来left去找数,当left找到了比key大的数,此时将找到的数放到坑位上,自己形成一个坑位,以此类推,直到left和right相遇则结束。最后将key填充坑位上,即可保证key左边的值比key都小,key右边的值都比key大。
2. 单排的代码实现
int PartSort(int* a, int left, int right)
{
assert(a);
int key = a[left];
// 初始化坑位
int pit = left;
while (left < right)
{
while (left<right && a[right]>=key)
{
right--;
}
// 程序走到这里时,right找到了比key小的值
a[pit] = a[right];
pit = right;
// 让left走
while (left < right && a[left] <= key)
{
left++;
}
// 程序走到这里,说明left找到了比key大的值
a[pit] = a[left];
pit = left;
}
// 当left和right相遇的时候,退出循环,最终将key的值放在最后的坑位上
a[pit] = key;
return pit;
}
理解:上述代码中,首先第一个坑的位置是left,也就是key对应的位置,最后一次坑的位置一定是left和right相遇的位置,因为,每次在走的只能是left和right中的一个,不能是left和right同时走,假如是left去遇到right,那么说明此时的坑位就是right位置指向的,如果是right去遇见left,那么此时的坑位就是left指向的。我们会发现一个规律:当left在走的时候,坑位一定是right形成的,在靠后的位置,所以left要去找比key大的数,然后填充到坑位上,才能满足条件。当right在走的时候,坑位一定是left形成的,在靠前的位置,所以right要去找比key小的值放到坑位上。
3. 综合排序的实现
综合快速排序的实现需要利用分治算法思想,也就是需要对keyi的左右子区间进行递归使用单排,当所有的子区间都有序的时候,那么整个数据就是有序的。
- 代码实现
// 快排
void QuickSort(int* a, int begin, int end)
{
assert(a);
if (begin >= end)
{
// 判断区间的有效性
// 如果区间中只有一个数,那么此时默认是有序的,不需要进行单排
// 如果区间不存在,同样不能进行单排
return;
}
// 区间有效
// 进行单排
int keyi = PartSort(a, begin, end);
// 将原数组区间[begin,end]分为[begin,keyi-1],keyi,[keyi+1,end]
// 递归单排左右子区间,使每一个子区间都有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
4. 测试
- 测试代码
void TestQuickSort()
{
int a[] = { 9,8,7,6,5,4,3,2,1 };// 逆序
int size = sizeof(a) / sizeof(int);
QuickSort(a, 0,size-1);
PrintArr(a, size);
}
int main()
{
TestQuickSort();
return 0;
}
- 测试结果

三、前后指针法
1. 单排
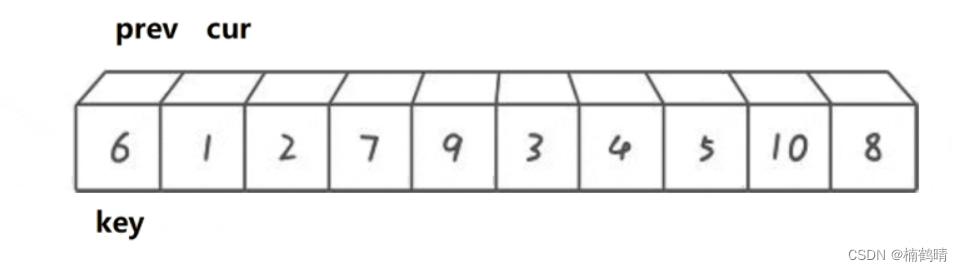
思想:这个方法的实现需要两个指针,同样需要一个位置的值来充当基准值,我们需要记录基准值的位置,记为
keyi。同样我们使用数组中第一个位置的元素作为基准值,在实现的过程中,需要两个指针来遍历,分别为:prev和cur,cur指针负责在前面进行探路,当cur指针找到了比key大的数,那么此时让prev++,交换prev和cur位置的值。如果cur指向的值比key小或者相等,那么只需要让cur继续向后走即可。这个方法本质就是让cur在前面找到比key大的数,然后将其放到前面的位置上。
2. 单排的代码实现
int PartSort(int* a, int left, int right)
{
assert(a);
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && a[++prev] != a[cur])
{
// 在这里面的prev的值是++后的值,也就是指向的值是比key大的,所以需要换到后面
Swap(&a[cur], &a[prev]);
}
cur++;
}
// 最终prev指向的值就是从头到尾最后一个比key小的数
Swap(&a[keyi], &a[prev]);
return prev;
}
在遍历排序的过程中,如果cur还没有遇到比key大的数,那么prev和cur是紧挨着的,如果cur遇到了比key大的数,那么cur和prev中会相差一些比key大的数。
- 如果cur还没有遇到比key大的数,那么prev和cur是紧挨着的:代码在执行的过程,如果cur找到的是比key小的数,那么
a[cur] < a[keyi]条件为真,此时会继续执行a[++prev] != a[cur],执行a[++prev] != a[cur]的时候首先会执行++prev,那么如果在此之前,cur从来没有找到比key大的数,那么prev和key是紧挨着的,所以a[++prev] != a[cur]这个条件就不成立,所以不会发生数据交换。总的结果就相当于prev和cur同步往后走。- 如果cur遇到了比key大的数,那么cur和prev中会相差一些比key大的数:代码在执行的过程,如果cur找到的是比key小的数,那么
a[cur] < a[keyi]条件为真,此时会继续执行a[++prev] != a[cur],执行a[++prev] != a[cur]的时候首先会执行++prev,那么如果在此之前cur从来没有找到比key大的数,那么prev和cur之间会相差一些比key大的数,所以prev和cur不是紧挨着的,所以a[++prev] != a[cur]这个条件就成立,此时才发生数据交换。
3. 综合排序的实现
综合快速排序的实现需要利用分治算法思想,也就是需要对keyi的左右子区间进行递归使用单排,当所有的子区间都有序的时候,那么整个数据就是有序的。
- 代码实现
// 快排
void QuickSort(int* a, int begin, int end)
{
assert(a);
if (begin >= end)
{
// 判断区间的有效性
// 如果区间中只有一个数,那么此时默认是有序的,不需要进行单排
// 如果区间不存在,同样不能进行单排
return;
}
// 区间有效
// 进行单排
int keyi = PartSort(a, begin, end);
// 将原数组区间[begin,end]分为[begin,keyi-1],keyi,[keyi+1,end]
// 递归单排左右子区间,使每一个子区间都有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
4. 测试
- 测试代码
void TestQuickSort()
{
int a[] = { 9,8,7,6,5,4,3,2,1 };// 逆序
int size = sizeof(a) / sizeof(int);
QuickSort(a, 0,size-1);
PrintArr(a, size);
}
int main()
{
TestQuickSort();
return 0;
}
- 测试结果

四、快排的时间复杂度
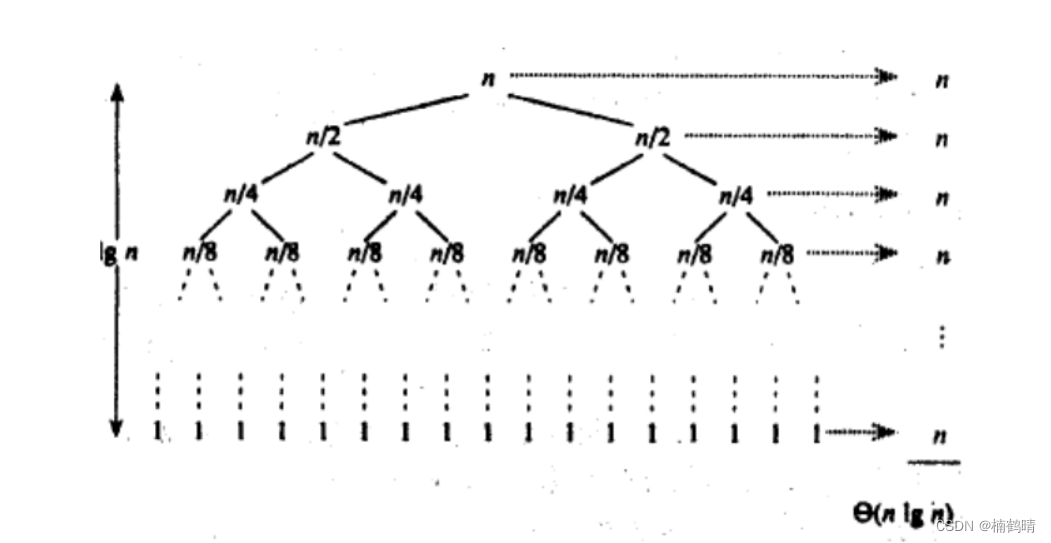
我们知道快速排序的过程,其实是利用单排+递归进行实现的,那么单排中,我们知道其实遍历的就是整个数组,所以单排中的时间复杂度为:O(N),所以快排的时间复杂度的问题就转化为递归的次数,快排中递归的情况和二叉树中的递归情况是比较类似的,所以假如递归的层数是h,总区间数为:N,那么就有N = 2^h-1,所以h = log2(N+1),即O(logN),所以快速排序的时间复杂度为:O(NlogN),这种情况是比较好的情况,就是每次的keyi都是数据的中位数,所以情况和二叉树类似,但是快速排序在处理实际问题的时候,每次keyi并不一定是中位数,最坏的情况就是每次的keyi是最左边的数或者最右边的数,那么这样递归的层数就会比较深了,假如有N个数据那么就需要递归N层,所以再加上单排的时间复杂度为:O(N),那么合起来这种情况的快速排序的时间复杂度就是O(NN)。
五、快排的优化
通过上面时间复杂度的分析,我们知道上面的代码在处理实际问题的时候,可能会出现最坏的情况,当出现最坏的情况时,时间复杂度为:O(N^2)。此时的效率就比较低了,所以我们需要对上面的代码进行优化,以解决这样的问题。
1. 三数取中
通过分析我们知道,最坏的情况就是当keyi是在最左边或者最右边的时候,也就是取到的keyi位置的值是区间中的最小值或者最大值时,效率最低,那么我们知道,如果我们取到的数据是数据中的最小值或者最大值,那么keyi最终就是在最前面或者最后面,那么分割出来的区间数就会比较多,最好的情况就是每次在进行区间分割的时候,也就是去keyi的时候,能够取到中间位置的值,所以我们可以考虑写一个算法来取代中间位置的值,需要参数就是数组,左右下标。
- 代码实现
// 第三种方法实现快排
int PartSort(int* a, int left, int right)
{
assert(a);
int min = GetMidIndex(a, left, right);
Swap(&a[min], &a[left]);
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && a[++prev] != a[cur])
{
// 在这里面的prev的值是++后的值,也就是指向的值是比key大的,所以需要换到后面
Swap(&a[cur], &a[prev]);
}
cur++;
}
// 最终prev指向的值就是从头到尾最后一个比key小的数
Swap(&a[keyi], &a[prev]);
return prev;
}
// 快排
void QuickSort(int* a, int begin, int end)
{
assert(a);
if (begin >= end)
{
// 判断区间的有效性
// 如果区间中只有一个数,那么此时默认是有序的,不需要进行单排
// 如果区间不存在,同样不能进行单排
return;
}
// 区间有效
// 进行单排
int keyi = PartSort(a, begin, end);
// 将原数组区间[begin,end]分为[begin,keyi-1],keyi,[keyi+1,end]
// 递归单排左右子区间,使每一个子区间都有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
// 三数取中
int GetMidIndex(int* a, int left, int right)
{
assert(a);
int mid = (left + right) / 2;
if (mid < left)
{
// mid left
if (a[right] < a[mid])
{
// right mid left
return mid;
}
else if(a[right]<a[left])
{
// mid right left
return right;
}
else
{
// mid left right
return left;
}
}
else
{
// left mid
if (a[right] > a[mid])
{
// left mid right
return mid;
}
else if (a[right] > a[left])
{
// left right mid
return right;
}
else
{
// right left mid
return left;
}
}
}
三数取中的好处就是在数据是有序或者逆序的时候,能够求出数据中的中位数作为key,后面有利用区间的分割。
2. 小区间优化
在上面的代码中,每一个子区间都是采用单趟排序递归进行排序的,当数据量很大的时候,后面的几层会产生很多的小区间,这些小区间又分别会建立栈帧,所以对系统的开销就会比较大。因此,我们可以考虑,当子区间不是特别大的时候,恶魔可以采用其他的排序算法对子区间中的数据进行排序,以减少系统栈帧的建立,从而减少系统开销。
- 代码实现
// 快排
void QuickSort(int* a, int begin, int end)
{
assert(a);
if (begin >= end)
{
// 判断区间的有效性
// 如果区间中只有一个数,那么此时默认是有序的,不需要进行单排
// 如果区间不存在,同样不能进行单排
return;
}
// 区间有效
if (end-begin+1<=10)
{
// 区间比较小的时候
InsertSort(a+begin, end - begin + 1);
}
else
{
// 区间比较大
// 进行单排
int keyi = PartSort(a, begin, end);
// 将原数组区间[begin,end]分为[begin,keyi-1],keyi,[keyi+1,end]
// 递归单排左右子区间,使每一个子区间都有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}
- 上面代码有很多细节需要注意:
- 区间的数据个数是end-begin+1,而不是end-begin。
- 在插入排序算法中的参数进行传递的时候,传的数组地址应该是
a+begin,而不是a。因为其中的begin和end都是数组下标,分割完之后就是代码数组下标中对应的范围的数据,那么你如果将参数传成a,那么数据的区间就变成从头开始的end-begin+1个数据了。正确的数据就应该是从a+begin的位置开始的end-begin+1个数据。
六、快排的非递归实现
上面学习的是快排的递归实现,快排的递归实现会存在一个问题,就是当递归的深度太深的时候就会出现栈溢出,所以我们需要学习如何将递归实现方式转化为非递归的实现方式,其实快排的本质就是不断地将原来数组进行分割,分割成很多的区间,那么我们只需要对每一个有效的区间进行单排,使每一个有效的区间都能够有序,那么总数居自然就是有序的。想要拿到每一个区间,必然需要拿到对应区间的下标,所以下标对于实现每一趟单排是非常重要的。快排的非递归实现还需要使用一个栈来进行辅助实现。代码如下:
// 栈的基本内容
typedef struct Stack
{
int* a;
int size;
int capacity;
}Stack;
// 基本操作的声明
void StackInit(Stack* st);
void StackPush(Stack* st, int val);
void StackPop(Stack* st);
int StackTop(Stack* st);
bool StackEmpty(Stack* st);
void StackDestroy(Stack* st);
//快排的非递归实现
void QuickSort(int* a, int left, int right)
{
assert(a);
// 通过栈来辅助实现
Stack st;
StackInit(&st);
// 将区间的左右下标入栈
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
// 出栈,拿到区间的左右下标
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int keyi = PartSort(a, left, right);
// [left,keyi-1] keyi [keyi+1,right]
// 将左右区间的左右下标入栈
if (left < keyi - 1)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
if (keyi + 1 < right)
{
StackPush(&st, keyi + 1);
StackPush(&st, right);
}
}
StackDestroy(&st);
}
![[Vulnhub] DC-9](https://img-blog.csdnimg.cn/ad84615158364f488eee07089271236e.png)





![[kubernetes]-k8s通过psp限制nvidia-plugin插件的使用](https://img-blog.csdnimg.cn/img_convert/fbeb9e31f760cd029406a2c286bdfe63.png)