目录
一、实验目的:
二、内容:棒球赛问题
三、实验要求
四、提交要求
————————
问题分析解释:
————————
算法简解:
Ford–Fulkerson 增广
Edmonds–Karp 算法
Dinic算法
Dinic和EK的区别:
代码:
一、实验目的:
- 掌握最大流算法思想。
- 学会用最大流算法求解应用问题。
二、内容:棒球赛问题
网络流和棒球赛淘汰问题 | Matrix67: The Aha Moments

1996 年 9 月 10 日,《旧金山纪事报》的体育版上登载了《巨人队正式告别 NL 西区比赛》一文,宣布了旧金山巨人队输掉比赛的消息。当时,圣地亚哥教士队凭借 80 场胜利暂列西区比赛第一,旧金山巨人队只赢得了 59 场比赛,要想追上圣地亚哥教士队,至少还得再赢 21 场比赛才行。然而,根据赛程安排,巨人队只剩下 20 场比赛没打了,因而彻底与冠军无缘(摘自http://www.matrix67.com/blog/archives/5190)。
有趣的是,报社可能没有发现,其实在两天以前,也就是 1996 年 9 月 8 日,巨人队就已经没有夺冠的可能了。那一天,圣地亚哥教士队还只有 78 场胜利,与洛杉矶道奇队暂时并列第一。此时的巨人队仍然是 59 场胜利,但还有 22 场比赛没打。因而,表面上看起来,巨人队似乎仍有夺冠的可能。然而,根据赛程安排
,圣地亚哥教士队和洛杉矶道奇队互相之间还有 7 场比赛要打,其中必有一方会获得至少 4 场胜利,从而拿到 82 胜的总分;即使巨人队剩下的 22 场比赛全胜,也只能得到 81 胜。由此可见,巨人队再怎么努力,也不能获得冠军了。
在美国职业棒球的例行赛中,每个球队都要打 162 场比赛(对手包括但不限于同一分区里的其他队伍,和同一队伍也往往会有多次交手),所胜场数最多者为该分区的冠军;如果有并列第一的情况,则用加赛决出冠军。在比赛过程中,如果我们发现,某支球队无论如何都已经不可能以第一名或者并列第一名的成绩结束比赛,那么这支球队就提前被淘汰了(虽然它还要继续打下去)。从上面的例子中可以看出,发现并且证明一个球队已经告败,有时并不是一件容易的事。
关于这个事情有一个有趣的故事,下面是一段对话:
“看到上周报纸上关于爱因斯坦的那篇文章了吗?……有记者请他算出三角比赛的数学公式。你知道,一支球队赢得了很多剩余的比赛,其他球队则赢这个赢了那个。这个比赛到底有多少种可能性?哪个球队更有优势?”
“他到底知道吗?”
“显然他知道的也不多。上周五他选择道奇队没有选巨人队。”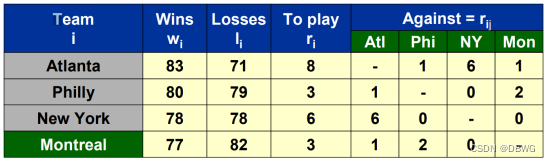
上面的表是四个球队的比赛情况,现在的问题是哪些球队有机会以最多的胜利结束这个赛季?可以看到蒙特利尔队因最多只能取得 80 场胜利而被淘汰,但亚特兰大队已经取得 83 场胜利,蒙特利尔队因为wi + ri < wj 而被淘汰。费城队可以赢83场,但仍然会被淘汰。 。 。如果亚特兰大输掉一场比赛,那么其他球队就会赢一场。所以答案不仅取决于已经赢了多少场比赛,还取决于他们的对手是谁。
请利用最大流算法给出上面这个棒球问题的求解方法。
三、实验要求
1. 解释流网络的构造原理。
2. 解释为什么最大流能解决这个问题。
3.给出上面四个球队的求解结果。
4. 尽可能实验优化的最大流算法。
四、提交要求
1. 在blackboard提交电子版实验报告,注意实验报告的书写,整体排版。
2. 实验报告的实验步骤部分需详细给出算法思想与实现代码之间的关系解释,不可直接粘贴代码(直接粘贴代码者视为该部分内容缺失)。
3. 实验报告中要求证明该算法的关键定理,并说明这些定理所起的作用。
4. 源代码作为实验报告附件上传。
5. 在实验课需要现场运行验证并讲解PPT。
————————
问题分析解释:
如果把每个单位的流量理解成一个一个的胜局,那么网络流也就可以理解为这些胜局的来源和去向。

编号:

要判断一个队伍是否有机会以最多的胜利结束这个赛季,只需让他全胜,然后分配其他队伍,看能否是最大值。
即在其余队伍都不超过这只队伍最高得分的前提下,比赛能否比完,如果能比完,这支队伍确实有机会获胜。
如果比不完(即此时无论如何分配,不管谁赢,都会超过这只队伍),那么这支队伍就无法取胜。所以我们可以用最大流来解决这个问题
让Atl接下来比赛全胜:

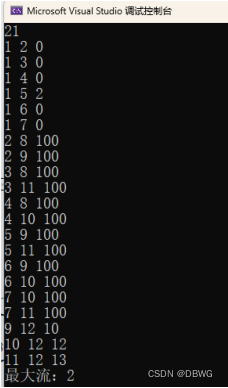 可以流完。
可以流完。



————————
算法简解:
最大流 - OI Wiki
一条从源点 s 到汇点 t 的路径称为增广路。
对于一条增广路,给每一条边 都加上等量的流量,以令整个网络的流量增加,这一过程被称为增广。
最大流的求解可以被视为若干次增广分别得到的流的叠加。
—————
Ford–Fulkerson 增广
Ford–Fulkerson 增广是计算最大流的一类算法的总称。该方法运用贪心的思想,通过寻找增广路来更新并求解最大流。
步骤:
1.寻找任意一条增广路
2.取增广路中最小容量作为本次增广流量
3.添加反向边——负流量 (反向边容量为0,此时 $$容量 - 负流量$$ 为正值)
时间复杂度:
上界:总边数*求得的最大流
对于反向边的理解:
我们当前的增广并不是最优的,需要调整,调整即把原来走过去的一部分“反悔”重新选择路径。反向边实则实现了这样的方式——别的增广路也能走这里,那么之前的可以换个路径走。所以可以走更多的增广路。
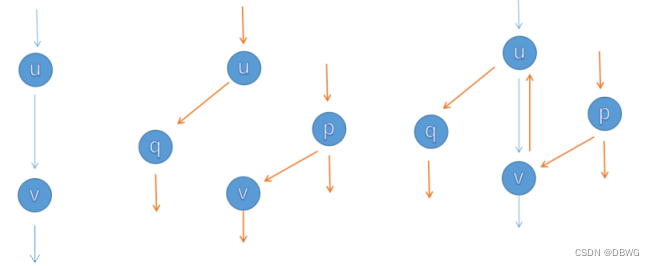
Edmonds–Karp 算法
13-3: Edmonds-Karp Algorithm 寻找网络最大流_哔哩哔哩_bilibili
Edmonds–Karp 算法其实就是优化了 Ford–Fulkerson 增广,在最开始找增广时,不去随意找,而是用Bfs找最短的。
时间复杂度为O(|V||E|)
迭代次数:在最坏的情况下,每次 BFS 都会减少至少一条边的容量,因此算法的迭代次数不会超过边数 E。
由于每次 BFS 的时间复杂度是 O(V + E),并且迭代次数最多是 E,因此 Edmonds-Karp 算法的总时间复杂度是 O(E * (V + E))
Dinic算法
13-4: Dinic's Algorithm 寻找网络最大流_哔哩哔哩_bilibili
分层概念:
 BFS 来构建分层图。
BFS 来构建分层图。
Dinic:


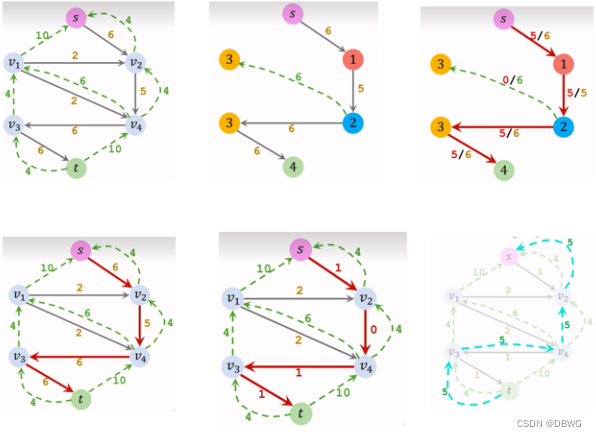
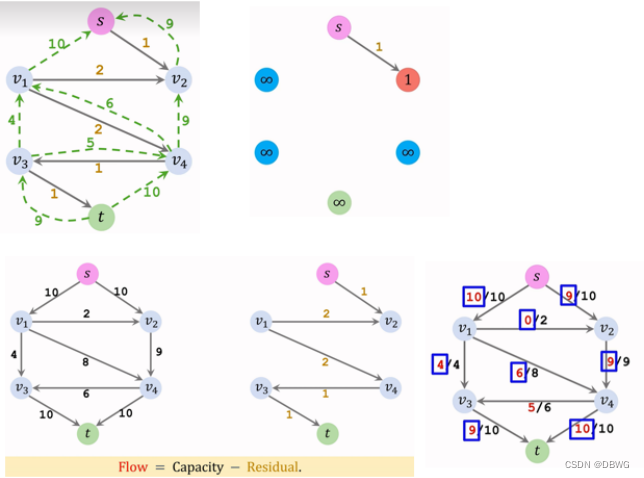
时间复杂度最坏为 O(m*n*n)
最多需要n-1轮,每轮BFS+DFS是O(m*n)
Dinic 算法会重复执行 BFS 和 DFS,直到无法找到增广路径为止。在最坏的情况下,每次迭代都会减少至少一条边的容量,因此迭代次数不会超过 E。

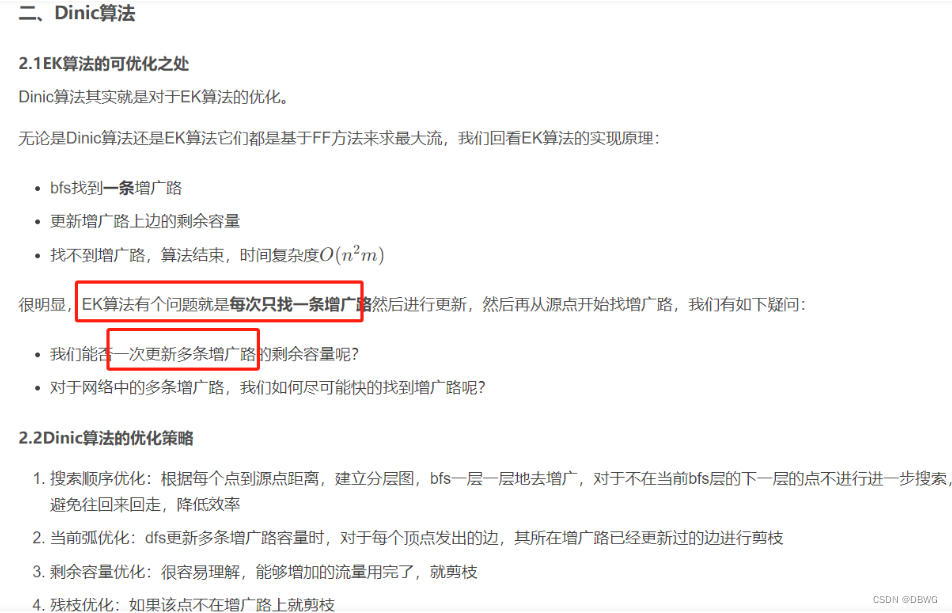
Dinic和EK的区别:
Dinic比EK更优,是因为Dinic一次分层后会把一层的增广路径都给找到。
代码:
直接粘的OI WIKI的板子:
#include <bits/stdc++.h>
using namespace std;
const int INF = std::numeric_limits<int>::max();
#define maxn 250
#define N 250
#define INF 0x3f3f3f3f
#define ll long long
struct Edge {
int from, to, cap, flow;
Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};
struct EK {
int n, m; // n:点数,m:边数
vector<Edge> edges; // edges:所有边的集合
vector<int> G[maxn]; // G:点 x -> x 的所有边在 edges 中的下标
int a[maxn], p[maxn]; // a:点 x -> BFS 过程中最近接近点 x 的边给它的最大流
// p:点 x -> BFS 过程中最近接近点 x 的边
void init(int n) {
for (int i = 0; i < n; i++) G[i].clear();
edges.clear();
}
void AddEdge(int from, int to, int cap) {
edges.push_back(Edge(from, to, cap, 0));
edges.push_back(Edge(to, from, 0, 0));
m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
int Maxflow(int s, int t) {
int flow = 0;
for (;;) {
memset(a, 0, sizeof(a));
queue<int> Q;
Q.push(s);
a[s] = INF;
while (!Q.empty()) {
int x = Q.front();
Q.pop();
for (int i = 0; i < G[x].size(); i++) { // 遍历以 x 作为起点的边
Edge& e = edges[G[x][i]];
if (!a[e.to] && e.cap > e.flow) {
p[e.to] = G[x][i]; // G[x][i] 是最近接近点 e.to 的边
a[e.to] =
min(a[x], e.cap - e.flow); // 最近接近点 e.to 的边赋给它的流
Q.push(e.to);
}
}
if (a[t]) break; // 如果汇点接受到了流,就退出 BFS
}
if (!a[t])
break; // 如果汇点没有接受到流,说明源点和汇点不在同一个连通分量上
for (int u = t; u != s;
u = edges[p[u]].from) { // 通过 u 追寻 BFS 过程中 s -> t 的路径
edges[p[u]].flow += a[t]; // 增加路径上边的 flow 值
edges[p[u] ^ 1].flow -= a[t]; // 减小反向路径的 flow 值
}
flow += a[t];
}
return flow;
}
};
struct MF {
struct edge {
int v, nxt, cap, flow;
} e[N];
int fir[N], cnt = 0;
int n = 249, S = 1, T = 12;
ll maxflow = 0;
int dep[N], cur[N];
void init() {
memset(fir, -1, sizeof fir);
cnt = 0;
}
void addedge(int u, int v, int w) {
e[cnt] = { v, fir[u], w, 0 };
fir[u] = cnt++;
e[cnt] = { u, fir[v], 0, 0 };
fir[v] = cnt++;
}
bool bfs() {
queue<int> q;
memset(dep, 0, sizeof(int) * (n + 1));
dep[S] = 1;
q.push(S);
while (q.size()) {
int u = q.front();
q.pop();
for (int i = fir[u]; ~i; i = e[i].nxt) {
int v = e[i].v;
if ((!dep[v]) && (e[i].cap > e[i].flow)) {
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[T];
}
int dfs(int u, int flow) {
if ((u == T) || (!flow)) return flow;
int ret = 0;
for (int& i = cur[u]; ~i; i = e[i].nxt) {
int v = e[i].v, d;
if ((dep[v] == dep[u] + 1) &&
(d = dfs(v, min(flow - ret, e[i].cap - e[i].flow)))) {
ret += d;
e[i].flow += d;
e[i ^ 1].flow -= d;
if (ret == flow) return ret;
}
}
return ret;
}
void dinic() {
while (bfs()) {
memcpy(cur, fir, sizeof(int) * (N));
maxflow += dfs(S, INF);
}
}
} mf;
int main()
{
int n;
cin >> n;
mf.init();
for (int i = 0; i < n; i++)
{
int f, t, c;
cin >> f >> t >> c;
mf.addedge(f, t, c);
}
mf.dinic();
cout << "最大流:" << mf.maxflow << endl;
return 0;
}