42. 接雨水*
力扣链接
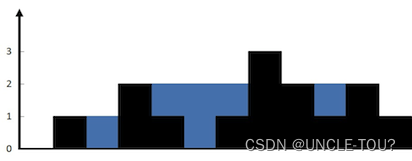
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
思路1 暴力
按列来计算。每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中,较矮的那个柱子的高度。
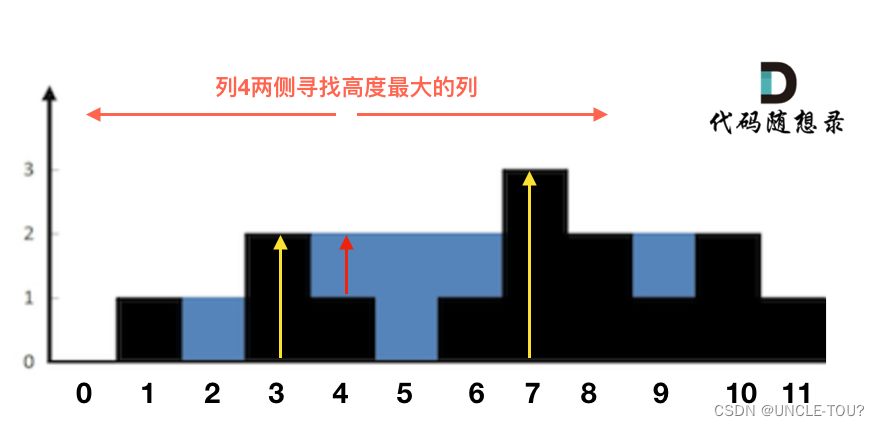
即
h = min(lHeight, rHeight) - height
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
for i in range(len(height)):
if i == 0 or i == len(height)-1: continue # 如果是两端则不处理
lHight = height[i-1]
rHight = height[i+1]
for j in range(i-1):
if height[j] > lHight:
lHight = height[j] # 找到左侧最高的
for k in range(i+2,len(height)):
if height[k] > rHight:
rHight = height[k] # 找到右侧最高的
res1 = min(lHight,rHight) - height[i]
if res1 > 0:
res += res1
return res
但是这样会超时
思路2 双指针优化
把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
对当前水柱i,他左边最高的柱子为maxLeft[i],右边最高的柱子为maxRight[i]
maxLeft[i] = max(height[i], maxLeft[i - 1])
maxRight[i] = max(height[i], maxRight[i + 1]);
class Solution:
def trap(self, height: List[int]) -> int:
maxleft = [0] * len(height)
maxright = [0] * len(height)
# 记录左侧最大柱子高度
maxleft[0] = height[0]
for i in range(len(height)):
maxleft[i] = max(height[i], maxleft[i-1])
# 记录右侧最大柱子高度
maxright[-1] = height[-1]
for i in range(len(height)-2, -1, -1):
maxright[i] = max(height[i], maxright[i+1])
res = 0
for i in range(len(height)):
res1 = min(maxleft[i],maxright[i]) - height[i]
if res1 > 0:
res += res1
return res
思路3 单调栈

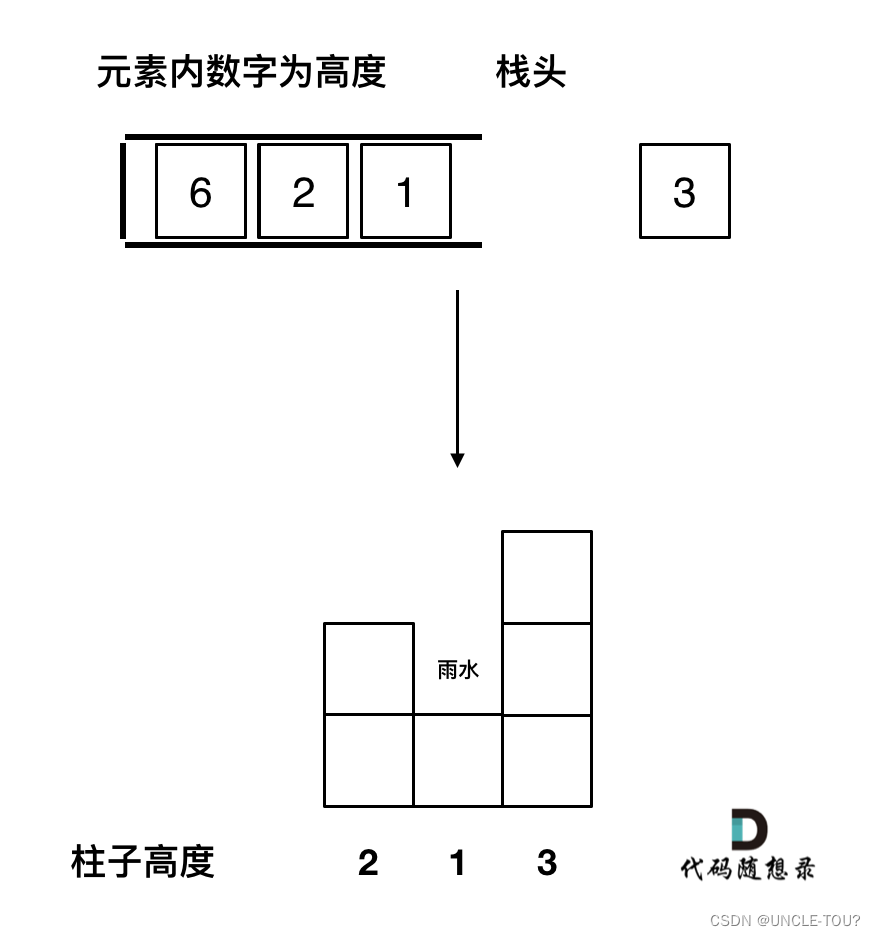
将每条柱子下标依次压栈
一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
求一个元素右边第一个更大元素,单调栈就是递增的;
求一个元素右边第一个更小元素,单调栈就是递减的。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
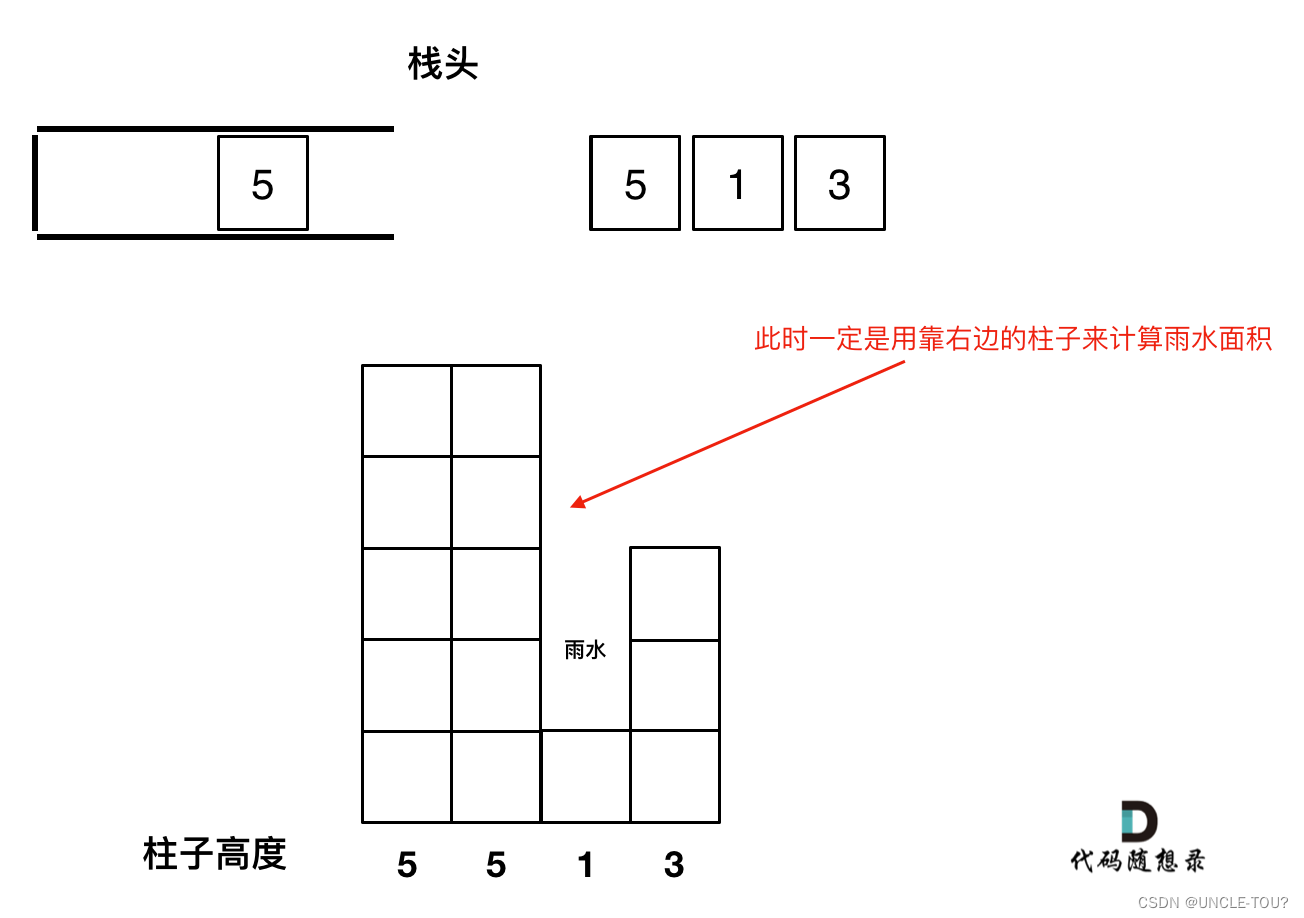
有三种情况:
情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子压栈,然后遍历height。
如果当前柱子低于栈顶,则入栈(因为要保持栈顶方向的递减)
如果当前柱子等于栈顶,则更新栈顶元素,先出栈再压栈
如果当前柱子高于栈顶,则出栈,记为mid(遇到凹槽了),此时栈顶为凹槽左,当前元素为凹槽右
显而易见,水的高度和宽度为:
h = min(height[st.pop()],height[i])-height[mid] # min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
w = i - st.top() - 1 # 凹槽右边的下标 - 凹槽左边的下标 - 1
class Solution:
def trap(self, height: List[int]) -> int:
stack = [0]
res = 0
for i in range(len(height)):
if height[i]<height[stack[-1]]:
stack.append(i)
elif height[i] == height[stack[-1]]:
stack.pop()
stack.append(i)
else:
while stack and height[i] > height[stack[-1]]:
mh = height[stack[-1]]
stack.pop()
if stack:
rh = height[i]
lh = height[stack[-1]]
h = min(rh, lh) - mh
w = i - stack[-1] -1
res += h*w
stack.append(i)
return res
84.柱状图中最大的矩形
力扣链接
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
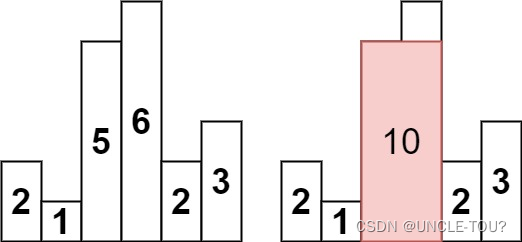
思路1 双指针
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
size = len(heights)
minleft = [0] * size
minright = [0] * size
# 记录每个柱子左边第一个矮子
minleft[0] = -1# 防止死循环
for i in range(size):
t = i-1
while t>=0 and heights[t]>=heights[i]: #不断向左寻找,没找到就尝试这个高柱子自己的次级柱子
t = minleft[t]
minleft[i] = t
# 记录每个柱子右边第一个矮子
minright[-1] = size
for i in range(size-2, -1, -1):
t = i+1
while t<size and heights[t]>=heights[i]: #不断向右寻找,没找到就尝试这个高柱子自己的次级柱子
t = minright[t]
minright[i] = t
res = 0
for i in range(size):
res1 = heights[i] * (minright[i] - minleft[i] - 1)
res = max(res1,res)
return res
思路2 单调栈
本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序
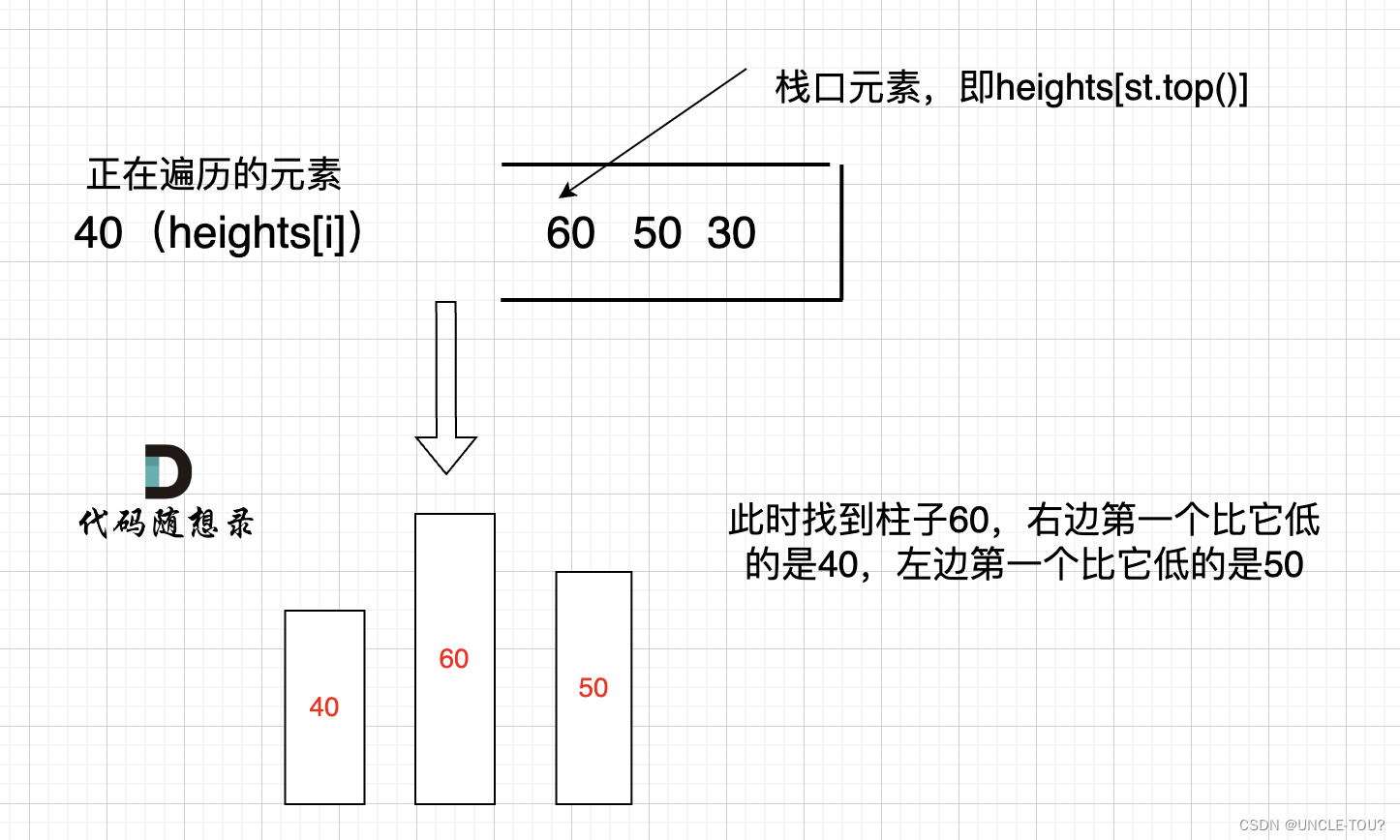
逻辑和接雨水差不多,就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度。
找每个柱子左右侧的第一个高度值小于该柱子的柱子
单调栈:栈顶到栈底:从大到小(每插入一个新的小数值时,都要弹出先前的大数值)
栈顶,栈顶的下一个元素,即将入栈的元素:这三个元素组成了最大面积的高度和宽度
有三种情况:
情况一:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
情况三:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
此外,还需要在height首尾各加一个0,以防跳过
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
res = 0
stack = [0]
heights.insert(0,0)
heights.append(0)
for i in range(1, len(heights)):
if heights[i] > heights[stack[-1]]:
stack.append(i)
elif heights[i] == heights[stack[-1]]:
stack.pop()
stack.append(i)
else:
while stack and heights[i] < heights[stack[-1]]:
mid = stack[-1]
stack.pop()
if stack:
left = stack[-1]
right = i
w = right - left - 1
h = heights[mid]
res = max(res, w * h)
stack.append(i)
return res