递归求解问题的分解过程，去的过程叫“递”，回来的过程叫“归”。

eg.电影院第几排？

f(n) = f(n-1) + 1
其中,f(1) = 1

根据递推公式，实现递归代码

public int f(int n) {
    if (n == 1) return 1;
    return f(n-1) + 1;
}

递归需要满足的三个条件

1. 一个问题的解可以分解为几个子问题的解；

2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样；

3. 存在递归终止条件

如何编写递归代码？

eg.假设有n个台阶，每次可以跨1个或2个台阶，请问走这n个台阶有多少种走法？

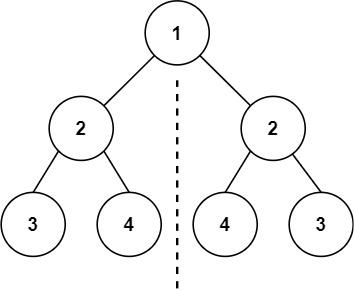
可以根据第一步的走法把所有走法分为两类：

第一类是第一步走了1个台阶；

第二类是第一步走了2个台阶

因此，有如下递推公式：

f(n) = f(n-1) + f(n-2)

递归终止条件，假设只有f(1) = 1

n = 2时，f(2) = f(1) + f(0)，这样还需要f(0) = 1，但是不符合逻辑

可以把f(2) = 2作为一个终止条件

f(1) = 1
f(2) = 2
f(n) = f(n-1) + f(n-2)

递归代码要警惕堆栈溢出

函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时出栈。系统栈或者虚拟栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

递归代码要警惕重复计算

public int f(n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    
    if (hasSolvedCache.containsKey(n)) {
        return hasSolvedCache.get(n);
    }
    
    int ret = f(n-1) + f(n-2);
    hasSolvedCache.put(n, ret);
    return ret;
}