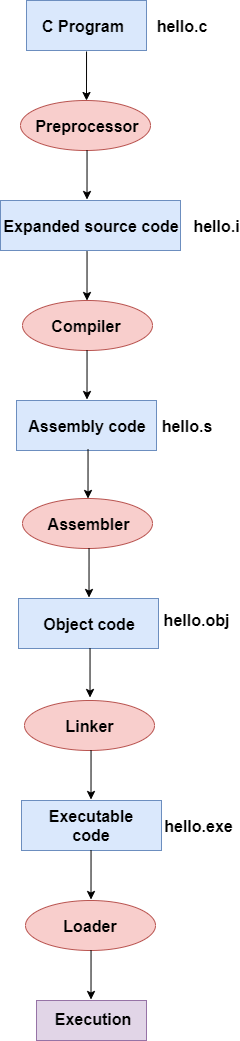
Lecture 15: Ray Tracing 3 (Light Transport & Global Illumination
- 一、BRDF 双向反射分布函数
- 定义
- 二、反射方程 Reflection Equation
- 三、渲染方程
- 1.重写反射方程
- 2.当其他的点反射的radiance作为入射
一、BRDF 双向反射分布函数
定义
- 计算不同的反射方向上会分布多少能量,描述了光线从特定方向入射到表面后,反射到各个方向的比例
-
f
r
f_{r}
fr(
ω
i
ω_{i}
ωi
→
\rightarrow
→
ω
r
ω_{r}
ωr) =
d
L
r
dL_{r}
dLr(
ω
r
ω_{r}
ωr) /
d
E
i
dE_{i}
dEi(
ω
i
ω_{i}
ωi) =
d
L
r
dL_{r}
dLr(
ω
r
ω_{r}
ωr) /
L
i
L_{i}
Li(
ω
i
ω_{i}
ωi)
c
o
s
θ
i
cosθ_{i}
cosθi
d
ω
i
dω_{i}
dωi
- f r f_{r} fr( ω i ω_{i} ωi → \rightarrow → ω r ω_{r} ωr) 为BRDF的值,表示从方向 ω i ω_{i} ωi到 ω r ω_{r} ωr方向
- d L r dL_{r} dLr( ω r ω_{r} ωr): ω r ω_{r} ωr方向 反射光线的光亮度(光通量)
- d E i dE_{i} dEi( ω i ω_{i} ωi) : ω i ω_{i} ωi方向入射光线的辐照度,等于 L i L_{i} Li( ω i ω_{i} ωi) c o s θ i cosθ_{i} cosθi d ω i dω_{i} dωi
-
c
o
s
θ
i
cosθ_{i}
cosθi:入射光线方向与表面法线之间夹角的余弦值
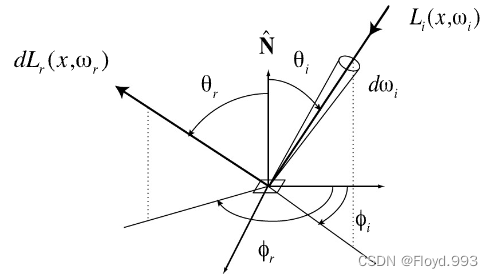
二、反射方程 Reflection Equation
- 任何不同方向入射,在某一反射方向的能量和
- L r ( p , ω r ) L_{r}( p, ω_{r}) Lr(p,ωr) = ∫ H 2 f r ( p , ω i → ω r ) L i ( p , ω i ) c o s θ i d ω i \int_{H^2}^{} f_{r}( p , ω_{i} \rightarrow ω_{r}) L_{i}( p , ω_{i}) cosθ_{i} dω_{i} ∫H2fr(p,ωi→ωr)Li(p,ωi)cosθidωi
-
L
r
(
p
,
ω
r
)
L_{r}( p, ω_{r})
Lr(p,ωr) 取决于
L
i
(
p
,
ω
i
)
L_{i}( p , ω_{i})
Li(p,ωi) 入射光线强度
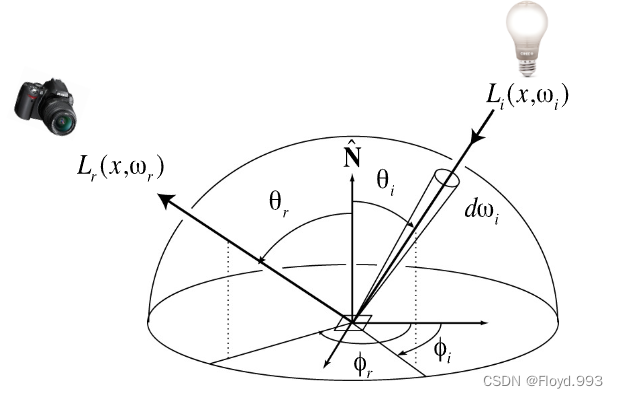
三、渲染方程
1.重写反射方程
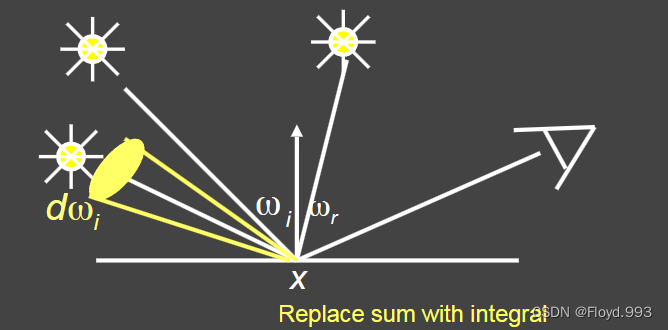
-
L
r
(
p
,
ω
r
)
L_{r}(p, ω_{r})
Lr(p,ωr) =
L
e
(
p
,
ω
o
)
L_{e}( p, ω_{o})
Le(p,ωo) +
∫
Ω
+
L
i
(
p
,
ω
i
)
f
r
(
p
,
ω
i
,
ω
r
)
(
n
⋅
ω
i
)
\int_{Ω^+}^{} L_{i}( p , ω_{i}) f_{r}( p , ω_{i} ,ω_{r}) ( n \cdot ω_{i})
∫Ω+Li(p,ωi)fr(p,ωi,ωr)(n⋅ωi)
- L e ( p , ω o ) L_{e}( p, ω_{o}) Le(p,ωo) 为自发光
- Σ \Sigma Σ 为将所有的光源求和
- L i ( p , ω i ) L_{i}( p , ω_{i}) Li(p,ωi) 为入射光(来自光源)
- f r ( p , ω i , ω r ) f_{r}( p , ω_{i} ,ω_{r}) fr(p,ωi,ωr) 为BRDF
- ( n ⋅ ω i ) ( n \cdot ω_{i}) (n⋅ωi) 入射角的余弦
2.当其他的点反射的radiance作为入射
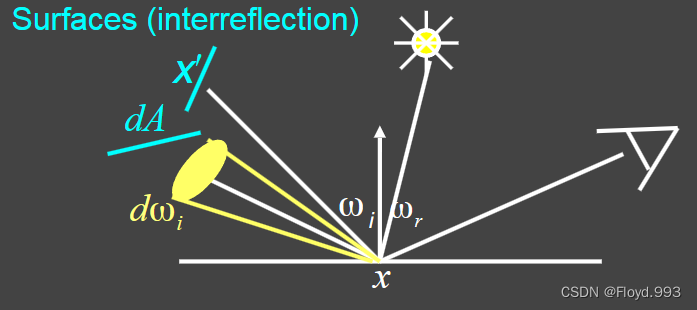
-
L
r
(
p
,
ω
r
)
L_{r}(p, ω_{r})
Lr(p,ωr) =
L
e
(
p
,
ω
o
)
L_{e}( p, ω_{o})
Le(p,ωo) +
∫
Ω
+
L
r
(
p
,
−
ω
i
)
f
r
(
p
,
ω
i
,
ω
r
)
(
n
⋅
ω
i
)
\int_{Ω^+}^{} L_{r}( p , -ω_{i}) f_{r}( p , ω_{i} ,ω_{r}) ( n \cdot ω_{i})
∫Ω+Lr(p,−ωi)fr(p,ωi,ωr)(n⋅ωi)
- L r ( p , − ω i ) L_{r}( p , -ω_{i}) Lr(p,−ωi) 为其他点的反射光(作为入射光)
- 方程中 L r ( p , ω r ) L_{r}(p, ω_{r}) Lr(p,ωr) 和 L r ( p , − ω i ) L_{r}( p , -ω_{i}) Lr(p,−ωi) 是不知道的,其他都知道
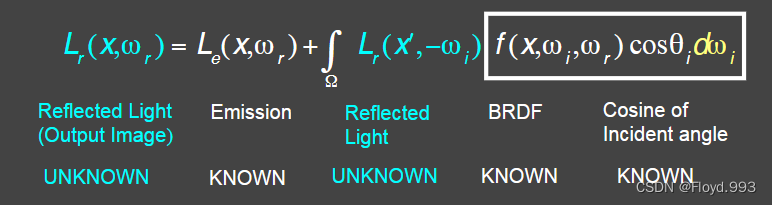
- 将方程改写为
l
(
u
)
=
e
(
u
)
+
∫
l
(
v
)
K
(
u
,
v
)
d
v
l(u) = e(u) + \int_{}^{} l(v) K(u,v)dv
l(u)=e(u)+∫l(v)K(u,v)dv (Fredholm 积分方程的第二类)
- l(u) 和 l(v) 是未知的
- 继续改写为 L = E + LK(改写为简单的矩阵方程,L和E为向量,K是光的传输矩阵)

- 推导后,
E
E
E为自发光,
K
E
KE
KE为直接光照,
K
2
E
K^2E
K2E为间接光照,…整体为全局光照
- E E E为自发光, K E KE KE为直接光照 ,此阶段光栅化可以做