大纲
这一节课程的大纲:

重点
对于这次课,重点是两个东西:

Motivating examples(为什么需要贝尔曼公式)
首先要明白,为什么 return 是重要的?

之前其实就说过,return 能够帮助我们评价一个策略是好还是坏,因此 return 的概念是非常重要的。
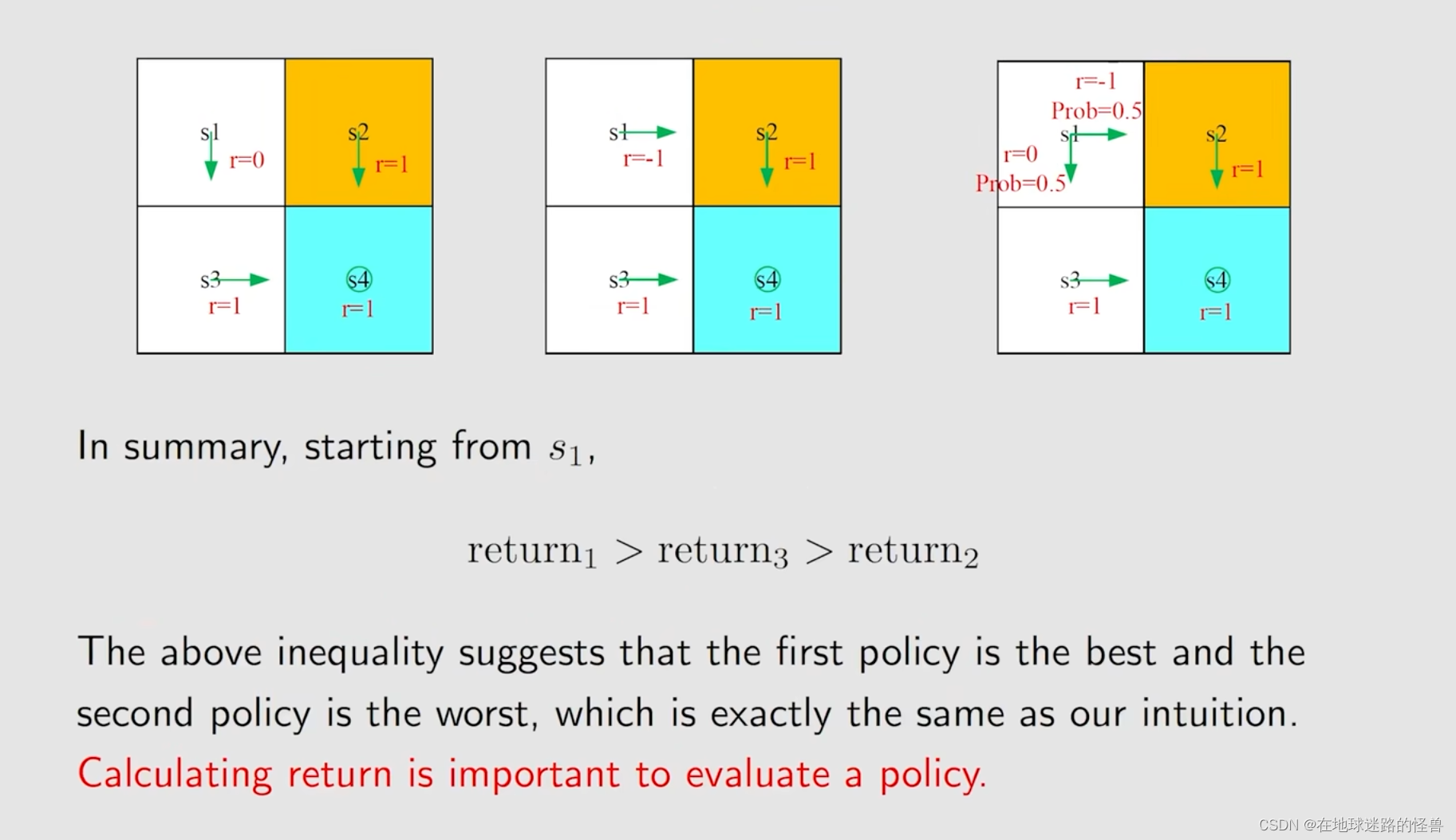
对于上图中的三种不同的策略,我们能够得到各个策略下所得到的 return 值:

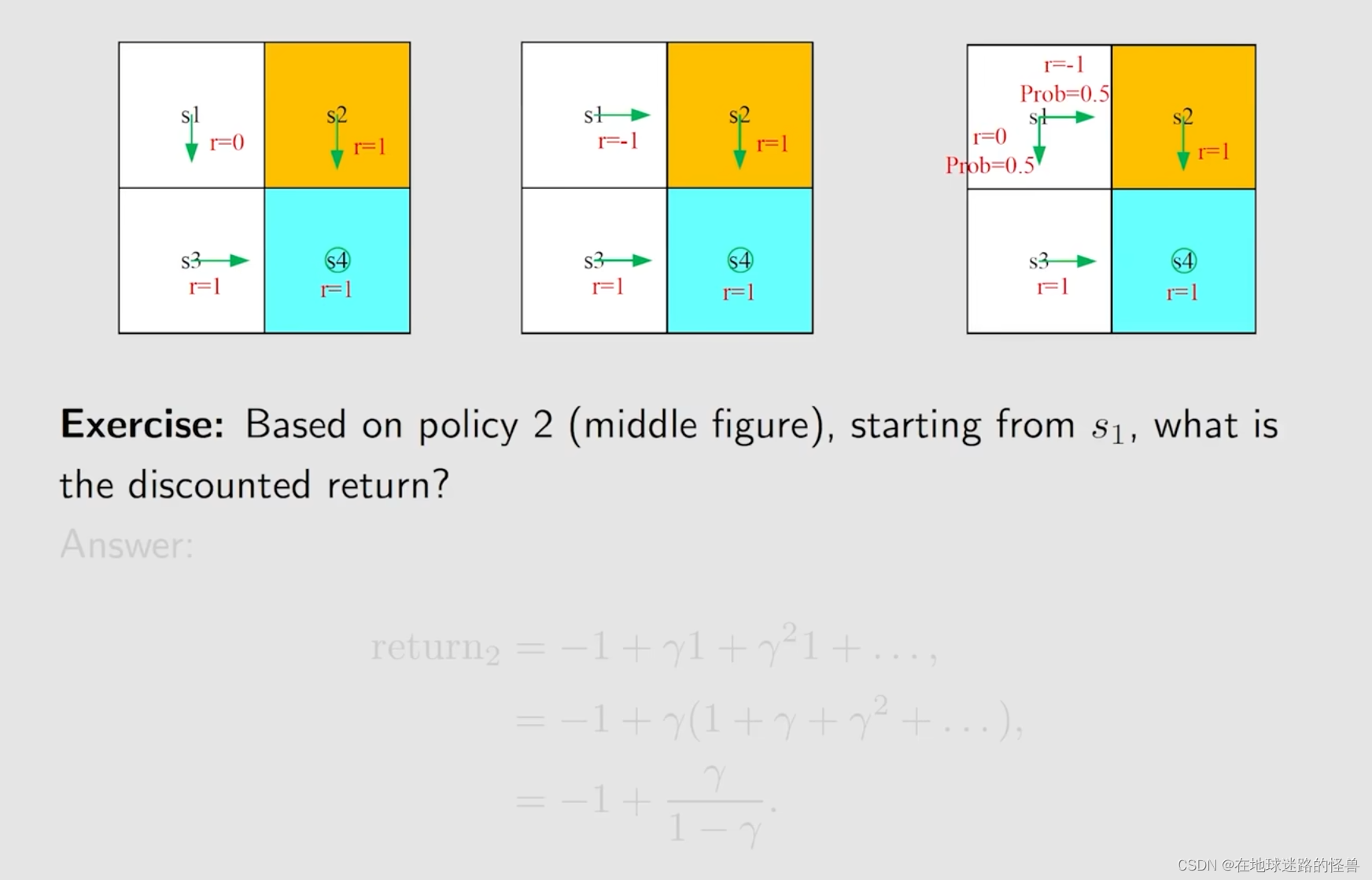
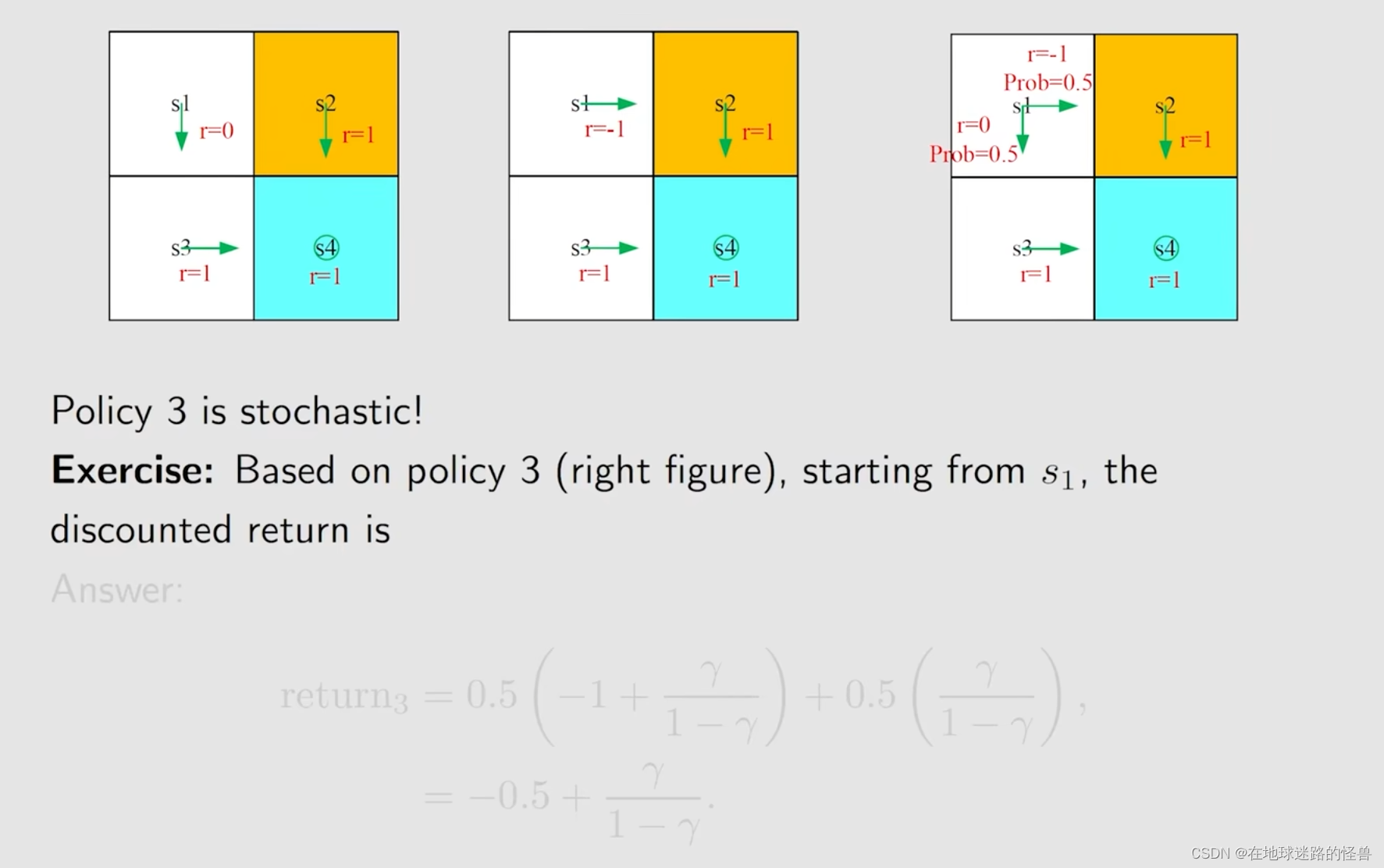
此时我们比较一下三个 return :
刚刚我们计算 return 使用的是 return 的本质定义,但实际上我们有更好的方法,来看下面的例子:
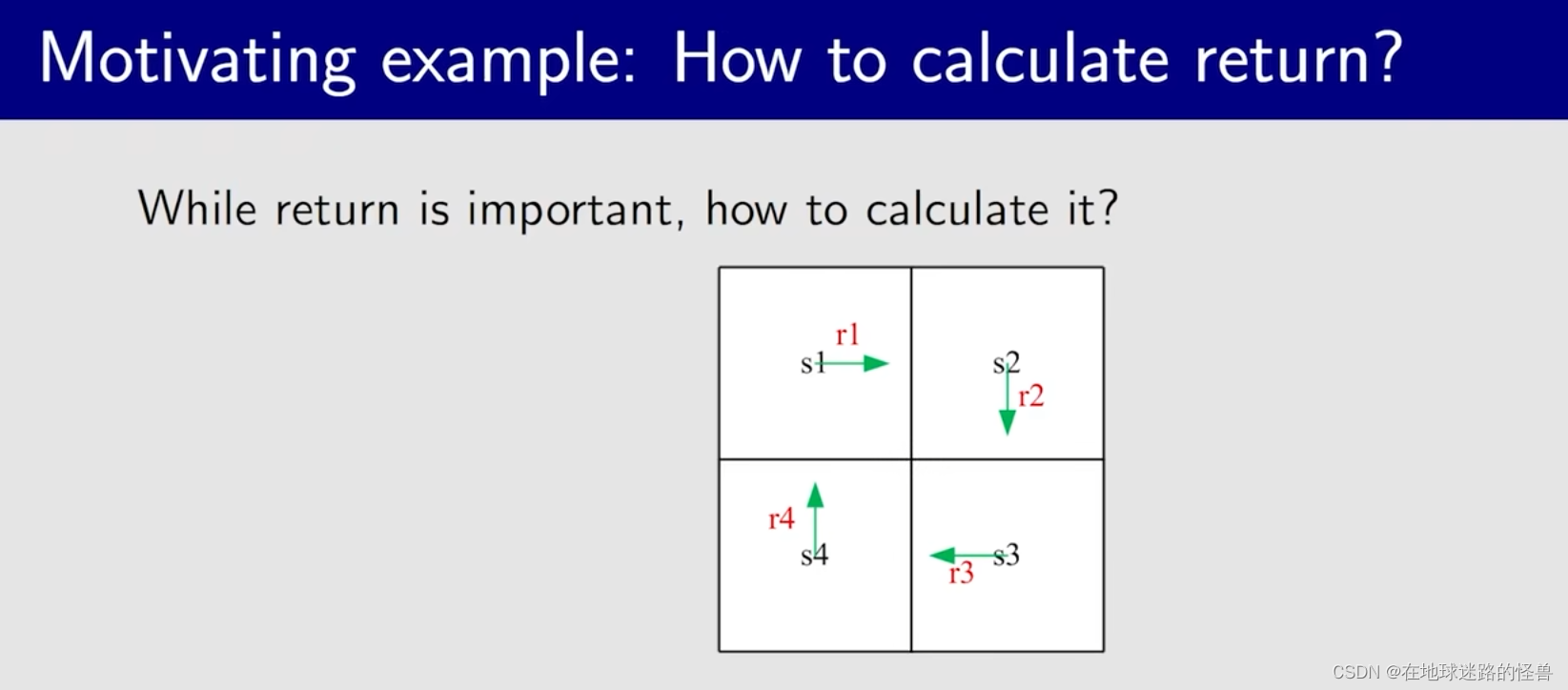
可以看见共有四个状态,然后每个状态 s 都有对应的策略(绿色箭头)和其对应的 return 值。
方法一就是使用我们刚刚的方式,也就是从定义出发,我们计算 return 的方式如下,引入 vi 用以表示 return 值:

而方法二就有意思多了:

从上式可以看出,从不同状态出发得到的 return,它是依赖于从其它状态出发所得到的 return 的,而这个 idea 在强化学习当中被称为 Bootsstrapping。
Bootsstrapping在不同的历史阶段有不同的含义,但现在的含义大概是表示 从自己出发然后去不断地迭代所得到的一些结果。
Bootstrapping使得强化学习算法能够在不完全依赖真实回报的情况下进行价值函数的更新,从而提高了算法的效率和灵活性。
然而,Bootstrapping也可能引入误差,因为价值函数的更新是基于之前的估计值,如果这些估计值本身就存在误差,那么误差可能会累积并影响算法的性能。
但此时有一个问题,我们要求解的就是 v,但居然还要事先知道 v?这怎么可能呢?
然而从数学的角度上看,是可以解决的。

注意:上图左侧中的关于 γv 这个矩阵的形式并不是顺序的v1、v2、v3、v4,因此我们需要使用一个矩阵(上图右侧的形式)来对其进行变换,变换后的结果就是顺序的了。
这个过程可以数学化为上图中的公式。
这个公式解也很容易解,只要具备一点线性代数的知识就能够求解,我们将 γPv 移动左边,然提出相同项 v,将(1-γP)求逆放到右边式子就可以进行求解了(γ、r 以及 P 我们都是已知的)。
而所得到的这个公式,就是我们本节课要提到的 贝尔曼公式:

但是这个贝尔曼公式是针对非常简单的、特别是 deterministic (确定性的过程)的一个情况,后面会介绍更加泛化的贝尔曼公式。
State value(什么是状态价值)
在介绍概念之前,需要先引入一些符号:

上图是一个简单的单步过程,St 表示当前状态,在当前状态下采取 At 的动作后得到的下一个 reward 就是 R(t+1),然后状态也跳转到了 S(t+1) 。
值得注意的是,有时候 R(t+1) 也会写成 Rt,从数学上来说没有什么本质区别,只是一个习惯问题,一般都是 R(t+1)。
另外在这个转换过程当中,所有的这些跳跃,它们都是由条件概率来决定的:

对于这样的单步过程如果连续起来,就成了多步的过程,也就形成了之前所说的 trajectory 的概念:

对于上图这样的 trajectory,我们当然可以对其求 discounted return,使用 G(t) 来表示。
有了这些准备,那么我们现在可以正式开始定义 State value 了:

State value 就是 G(t) 的 expectation 期望值,或者也可以叫 expected value 或者叫 mean,或者叫 average ,它们实际上都代表同一个意思,就是平均值。
,“期望”(expectation)通常指的是数学上的期望值,即随机变量的平均值或者是在概率分布下的加权平均。
期望一直是定量,它与总体的均值相等。但是均值可以是变量,因为取不同样本的时候均值可以不同。
实际上 State value 的全程是 State value function,我们使用 VΠ(s) 来代替 state value,其数学定义就是对 Gt 求 expectation 。但注意这是一个 条件期望,也就是当前的状态应该取一个具体的值 s。
return 和 state value 的联系
那么 return 和 state value 有什么区别和联系呢?
其实非常简单,return 是针对单个 trajectory 所求的,而 state value 则是对多个 trajectory 所求得的 return 和后再求平均值之后的结果。
如果从一个状态出发有可能得到多个 trajectory,这时候 return 和 state value 显然是有区别的;但是如果从一个状态出发一切都是确定性的,那么只能够得到一条 trajectory,那这时候从该状态出发所得到的 return 和 state value 就是一样的。
Bellman equation(贝尔曼公式)
贝尔曼公式推导

刚刚我们已经知道了 state value 是非常重要的,但是怎么计算 state value 呢?
贝尔曼公式就是用来计算 state value 的,其用一句话来阐述就是:它描述了不同状态的 state value 之间的关系。
接下来我们来推到 贝尔曼公式:





dynamic model 也称为 environment model,这又分为两种情况,一种是我们知道这个 model 进行求解(在本节以及下面几节课都是基于已知 model 的),还有一种是不知道 model,即使不知道 model 我们仍可以求出来 state value,这又被称为 model-free 的强化学习算法(这将在未来的课程当中介绍)。
接下来举一个例子来深入理解一下这个 贝尔曼公式:
我们考虑这样一个例子,在下图中我们由一个策略 Π(绿色箭头),我们要做的就是把这个问题当中所有的贝尔曼公式全部写出来:

说白了就是确定对于 s1 这个状态来说,其贝尔曼公式中各个概率项需要分析并且确定出来。

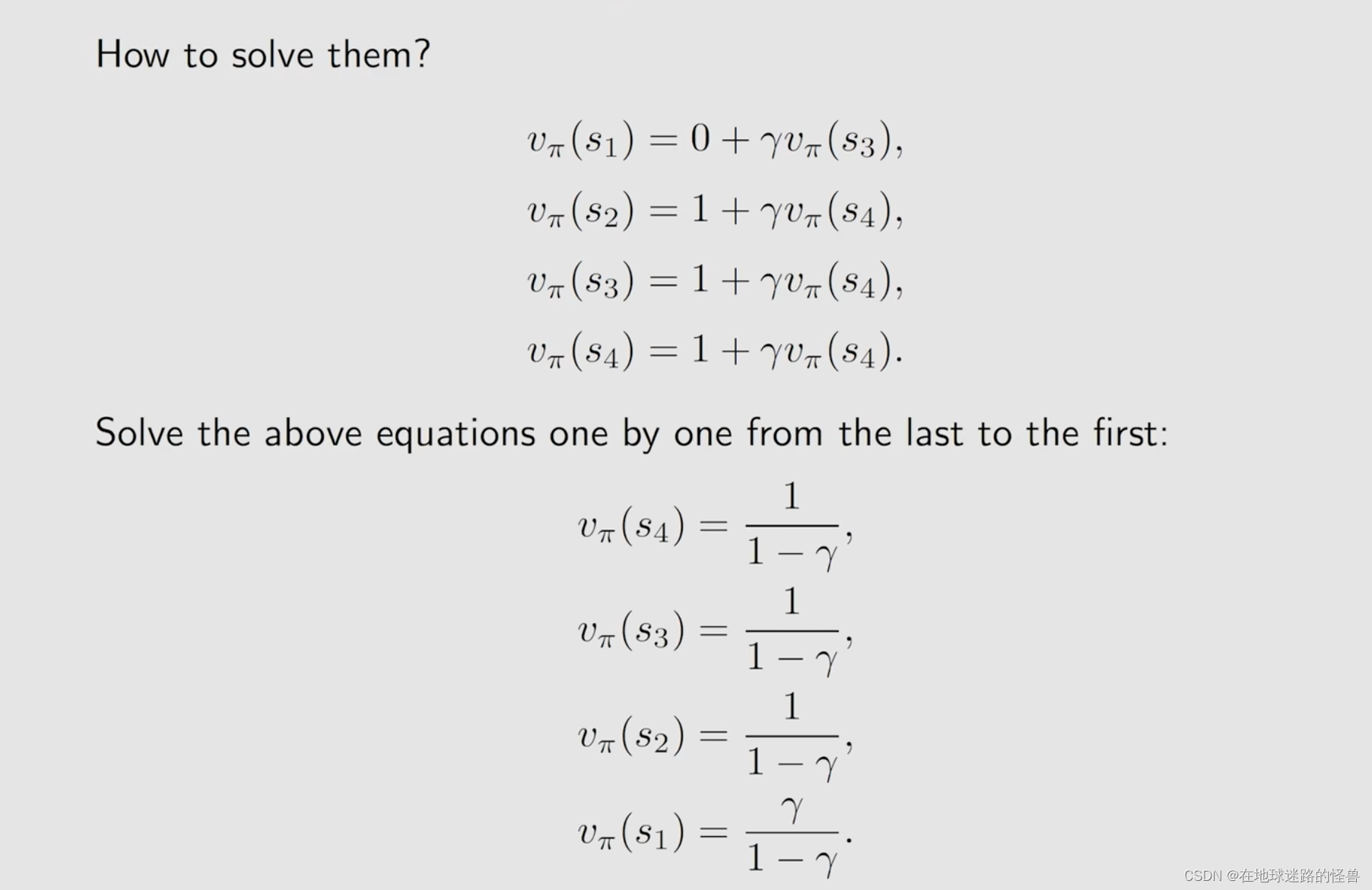

当我们计算出来 state value 之后,下一步实际上就可以去改进这个策略,这样慢慢地我们就可以得到最优的策略。
另一个例子:


贝尔曼公式:矩阵向量形式

之前说过,对于 n 个 state 那么就会有 n 个这样的贝尔曼公式。那么把所有的这些公式放在一起就能得到一组,这一组就可以整理成矩阵向量的形式,进而完成 贝尔曼公式 中对 state value 的求解。
如何得到这些公式的 矩阵向量形式:


举个例子来看一下,当有 4 个状态时所得到的 矩阵向量 形式如何:

另一个例子:

贝尔曼公式:求解 state values
首先回答一个问题,为什么需要求解 state value?
实际上给定一个 policy,然后我们会列出其贝尔曼公式,再进一步求解这个贝尔曼公式得到 state value。这么一个过程称为:policy evaluation。

policy evaluation 是 RL 中非常关键的一个问题,是非常基础的一个工具,只有能够去评价一个策略是好还是不好我们才能够去改进它最后才能找到最优策略。
因此求解贝尔曼公式进而得到 state value 是非常重要的问题。

上图中的第一行表达式就是我们刚刚推出的贝尔曼公式的 矩阵向量形式,求解有两种方式,一种是求解析解,如上图第二行表达式所示(通过第一行表达式,我们很容易能够推导出第二行表达式),但是这样做是复杂的,因为有一个求逆的过程,在状态空间非常大的时候,这种计算是困难且复杂的。
因此我们一般使用 迭代 的方式来完成求解,即上图中第三行表达式(左边是V(k+1),右边是 Vk )。假如带入 V0,那么自然就能得到 V1,然后带入 V1,则又能得到 V2,这样迭代下去就能得到一个序列,可以从数学上证明,当 K 趋向于无穷大的时候,Vk 就收敛到了 VΠ,而这个 VΠ 就是真实的 state value。

来看个例子,先看两种比较好的策略得到的 state values:

从上图的两种不同策略可以看出,对于不同的策略是能够得到相同的 state value 值的。
再来看两种不好的策略所导致的结果:

通过这些例子,我们明白了可以通过计算 state value 来评价一个策略究竟是好还是不好。
Action value(什么是行为价值)
在学习了 state value 之后学习 action value 就会容易一些,下面是二者之间的区别与联系:

action value 的定义:

action value 依赖于从哪个状态出发、以及是哪一个 action 来出发,另外它也依赖于策略 Π。

一个例子:


因此 action value 是非常重要的,因为在未来会关注在某一个状态其不同的 action,比较这些不同的 action,我们会选一个 action value 值最大的那个。
action value 如何计算?
第一种方法是知道了 state value,比如求解了一个 贝尔曼公式,然后从 state value 中计算出来 action value;
第二种方式是不计算 state value 而直接计算 action value,比如说通过数据的方式,此时就不再依赖于这个模型了(在未来都会介绍):
Summary(总结)