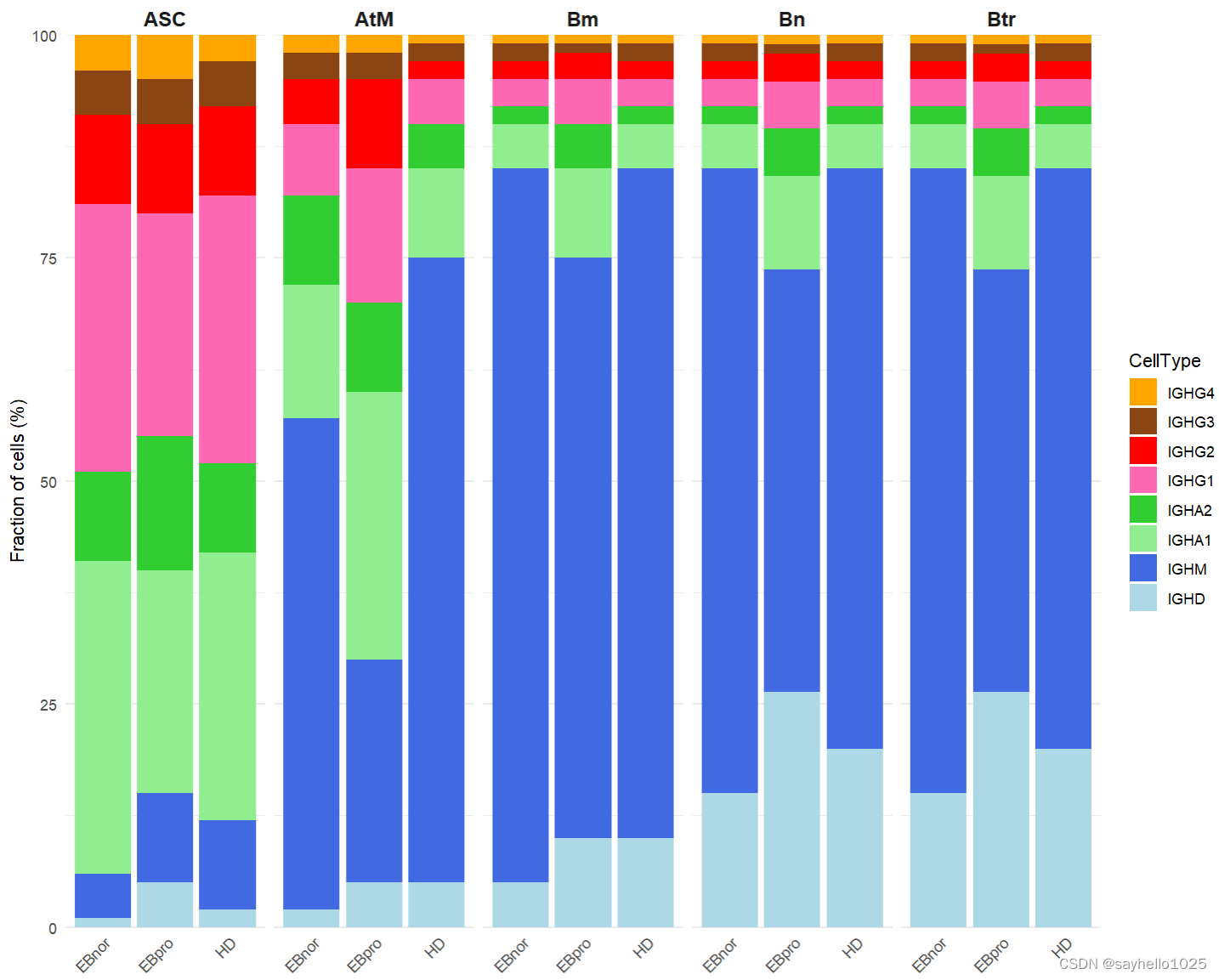
💬 写在前面:从现在开始,让我们正式设计和实现编程语言。首先,让我们扩展在之前定义的整数表达式语言,以便可以使用变量和条件表达式。
目录
0x00 文法结构
0x01 真假表达式:isZero E
0x02 let 表达式叠放
0x03 定义的规则
0x04 条件语句的使用
0x00 文法结构
扩展后的语言的文法结构如下,在整数表达式语言中增加了四种文法:
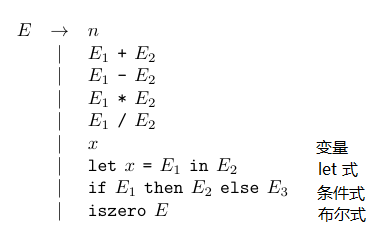
在程序中,可以在任意可以出现表达式的位置使用变量 (随机变量)
let =
in
是一个声明变量
的表达式。
它先将 的值赋给
,然后计算
的值。在此期间,变量
的有效范围是
。
if then
else
是一个条件表达式,其计算方式如下。
.
此后,我们约定符号 表示 true,符号
表示 false。
首先计算表达式 ,其结果必须是
或
。
- 如果
的值是
,则计算
- 如果
的值是
,则计算
。
0x01 真假表达式:isZero E
为了使用条件表达式,需要创建产生 真/假 的表达式,因此我们添加了语法:
它计算表达式 的值,如果值为 0,则计算为
,否则为
。
由于它类似于 OCaml 的语法,可以很容易感受到可以编写哪些程序,举几个例子:
下面是一个程序,首先变量 ,然后计算
的值,结果是 3
let x = 1 in x + 20x02 let 表达式叠放
在 let 表达式的 位置上可以放置另一个 let 表达式
let x = 1
in let y = 2
in x + y表达式 中,
和
分别代表 1 和 2,因此程序的计算结果是 3。
.
也可以在 let 表达式的 位置上放置另一个 let 表达式,如下所示。
let x = let y = 2
in y + 1
in x + 3表达式 let y = 2 in y + 1 的值为 3,将其命名为 后,计算表达式
的结果为 6。
在计算表达式 时,请注意变量
不可用。
变量 的作用范围仅限于表达式
,因此在其他地方无法使用。
因此,下面的程序在语法上没有问题,但在执行时会出现问题。
let x = let y = 2
in y + 1
in x + y0x03 定义的规则
可以多次使用相同的名称进行定义,如下所示。
let x = 1
in let y = 2
in let x = 3
in x + y
在最后一行计算 时,
表示最后定义的值 3,因此
的值是 5。
重新定义具有相同名称的变量并不会改变先前变量的值。
使用 let 定义变量并不是修改现有变量的值,而是创建一个新名称,在其作用域内具有意义。
例如下面的程序:
let x = 1
in let y = let x = 2
in x + x
in x + y上述程序计算的结果是 5。第一行定义变量 ,第二行定义的
。
因此第三行的 的值是 4,因此变量
的值为 4。
在最后一行的表达式 中,变量
指的是第一行定义的
,因此
的值为 5。
0x04 条件语句的使用
条件语句的使用如下所示。这是一个计算整数 1 的程序。
let x = 1
in let y = 2
in if iszero (x - 1) then y - 1 else y + 1.
现在,由于程序不仅可以计算整数,还可以计算真 / 假值,因此存在一些由于类型不匹配而无法执行的程序,即存在 类型错误 (type error) 的程序。例如,看下面的程序。
let x = 1
in let y = iszero x
in x + y加法是针对两个整数定义的操作,但由于 ,因此在计算
时会发生类型错误。
由于我们的语言目前没有静态类型系统,所以无法在执行前发现这类类型错误。
如果在运行过程中发生类型错误,程序将会因此而非正常终止。

📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2022.9.14
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 - R. Neapolitan, Foundations of Algorithms (5th ed.), Jones & Bartlett, 2015. - T. Cormen《算法导论》(第三版),麻省理工学院出版社,2009年。 - T. Roughgarden, Algorithms Illuminated, Part 1~3, Soundlikeyourself Publishing, 2018. - J. Kleinberg&E. Tardos, Algorithm Design, Addison Wesley, 2005. - R. Sedgewick&K. Wayne,《算法》(第四版),Addison-Wesley,2011 - S. Dasgupta,《算法》,McGraw-Hill教育出版社,2006。 - S. Baase&A. Van Gelder, Computer Algorithms: 设计与分析简介》,Addison Wesley,2000。 - E. Horowitz,《C语言中的数据结构基础》,计算机科学出版社,1993 - S. Skiena, The Algorithm Design Manual (2nd ed.), Springer, 2008. - A. Aho, J. Hopcroft, and J. Ullman, Design and Analysis of Algorithms, Addison-Wesley, 1974. - M. Weiss, Data Structure and Algorithm Analysis in C (2nd ed.), Pearson, 1997. - A. Levitin, Introduction to the Design and Analysis of Algorithms, Addison Wesley, 2003. - A. Aho, J. Hopcroft, and J. Ullman, Data Structures and Algorithms, Addison-Wesley, 1983. - E. Horowitz, S. Sahni and S. Rajasekaran, Computer Algorithms/C++, Computer Science Press, 1997. - R. Sedgewick, Algorithms in C: 第1-4部分(第三版),Addison-Wesley,1998 - R. Sedgewick,《C语言中的算法》。第5部分(第3版),Addison-Wesley,2002 |